LSTM及其变种及其克服梯度消失
本宝宝又转了一篇博文,但是真的很好懂啊:
写在前面:知乎上关于lstm能够解决梯度消失的问题的原因:

上面说到,LSTM 是为了解决 RNN 的 Gradient Vanish 的问题所提出的。关于 RNN 为什么会出现 Gradient Vanish,上面已经介绍的比较清楚了,本质原因就是因为矩阵高次幂导致的。下面简要解释一下为什么 LSTM 能有效避免 Gradient Vanish。
对于 LSTM,有如下公式
模仿 RNN,我们来计算 ,有
<img src="https://pic4.zhimg.com/v2-8eb676e7c1bac3eb131d8e0bf2f7db5b_b.png" data-rawwidth="147" data-rawheight="149" class="content_image" width="147">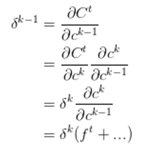
公式里其余的项不重要,这里就用省略号代替了。可以看出当 时,就算其余项很小,梯度仍然可以很好导到上一个时刻,此时即使层数较深也不会发生 Gradient Vanish 的问题;当
时,即上一时刻的信号不影响到当前时刻,则梯度也不会回传回去;
在这里也控制着梯度传导的衰减程度,与它 Forget Gate 的功能一致。
传统RNN,BPTT(BACK propagation through time)梯度回传时候会有连成,tanh【0,1】 sigmoid(0,1/4),导致梯度消失,虽然可以替换激活函数,RELU,但是LSTM可以解决呀
通常,数据的存在形式有语音、文本、图像、视频等。因为我的研究方向主要是图像识别,所以很少用有“记忆性”的深度网络。怀着对循环神经网络的兴趣,在看懂了有关它的理论后,我又看了Github上提供的tensorflow实现,觉得收获很大,故在这里把我的理解记录下来,也希望对大家能有所帮助。本文将主要介绍RNN相关的理论,并引出LSTM网络结构(关于对tensorflow实现细节的理解,有时间的话,在下一篇博文中做介绍)。
循环神经网络
RNN,也称作循环神经网络(还有一种深度网络,称作递归神经网络,读者要区别对待)。因为这种网络有“记忆性”,所以主要是应用在自然语言处理(NLP)和语音领域。与传统的Neural network不同,RNN能利用上”序列信息”。从理论上讲,它可以利用任意长序列的信息,但由于该网络结构存在“消失梯度”问题,所以在实际应用中,它只能回溯利用与它接近的time steps上的信息。
1. 网络结构
常见的神经网络结构有卷积网络、循环网络和递归网络,栈式自编码器和玻尔兹曼机也可以看做是特殊的卷积网络,区别是它们的损失函数定义成均方误差函数。递归网络类似于数据结构中的树形结构,且其每层之间会有共享参数。而最为常用的循环神经网络,它的每层的结构相同,且每层之间参数完全共享。RNN的缩略图和展开图如下,

尽管RNN的网络结构看上去与常见的前馈网络不同,但是它的展开图中信息流向也是确定的,没有环流,所以也属于forward network,故也可以使用反向传播(back propagation)算法来求解参数的梯度。另外,在RNN网络中,可以有单输入、多输入、单输出、多输出,视具体任务而定。
2. 损失函数
在输出层为二分类或者softmax多分类的深度网络中,代价函数通常选择交叉熵(cross entropy)损失函数,前面的博文中证明过,在分类问题中,交叉熵函数的本质就是似然损失函数。尽管RNN的网络结构与分类网络不同,但是损失函数也是有相似之处的。
假设我们采用RNN网络构建“语言模型”,“语言模型”其实就是看“一句话说出来是不是顺口”,可以应用在机器翻译、语音识别领域,从若干候选结果中挑一个更加靠谱的结果。通常每个sentence长度不一样,每一个word作为一个训练样例,一个sentence作为一个Minibatch,记sentence的长度为T。为了更好地理解语言模型中损失函数的定义形式,这里做一些推导,根据全概率公式,则一句话是“自然化的语句”的概率为
所以语言模型的目标就是最大化P(w1,w2,...,wT)。而损失函数通常为最小化问题,所以可以定义
那么公式展开可得
展开式中的每一项为一个softmax分类模型,类别数为所采用的词库大小(vocabulary size),相信大家此刻应该就明白了,为什么使用RNN网络解决语言模型时,输入序列和输出序列错了一个位置了。
3. 梯度求解
在训练任何深度网络模型时,求解损失函数关于模型参数的梯度,应该算是最为核心的一步了。在RNN模型训练时,采用的是BPTT(back propagation through time)算法,这个算法其实实质上就是朴素的BP算法,也是采用的“链式法则”求解参数梯度,唯一的不同在于每一个time step上参数共享。从数学的角度来讲,BP算法就是一个单变量求导过程,而BPTT算法就是一个复合函数求导过程。接下来以损失函数展开式中的第3项为例,推导其关于网络参数U、W、V的梯度表达式(总损失的梯度则是各项相加的过程而已)。
为了简化符号表示,记E3=−logp(w3|w1,w2),则根据RNN的展开图可得,
所以,
说明一下,为了更好地体现复合函数求导的思想,公式(2)中引入了变量W1,可以把W1看作关于W的函数,即W1=W。另外,因为s−1表示RNN网络的初始状态,为一个常数向量,所以公式(2)中第4个表达式展开后只有一项。所以由公式(2)可得,
简化得下式,
继续简化得下式,
3.1 E3关于参数V的偏导数
记t=3时刻的softmax神经元的输入为a3,输出为y3,网络的真实标签为y(1)3。根据函数求导的“链式法则”,所以有下式成立,
3.2 E3关于参数W的偏导数
关于参数W的偏导数,就要使用到上面关于复合函数的推导过程了,记zi为t=i时刻隐藏层神经元的输入,则具体的表达式简化过程如下,
类似于标准的BP算法中的表示,定义δmn=∂Em∂zn,那么可以得到如下递推公式,
那么,公式(7)可以转化为下式,
显然,结合公式(8)中的递推公式,可以递推求解出公式(9)中的每一项,那么E3关于参数W的偏导数便迎刃而解了。
3.3 E3关于参数U的偏导数
关于参数U的偏导数求解过程,跟W的偏导数求解过程非常类似,在这里就不介绍了,感兴趣的读者可以结合3.2的思路尝试着自己推导一下。
4. 梯度消失问题
当网络层数增多时,在使用BP算法求解梯度时,自然而然地就会出现“vanishing gradient“问题(还有一种称作“exploding gradient”,但这种情况在训练模型过程中易于被发现,所以可以通过人为控制来解决),下面我们从数学的角度来证明RNN网络确实存在“vanishing gradient“问题,推导公式如下,
大家应该注意到了,上面的式子中有一个连乘式,对于其中的每一项,满足si=activation(U×xi+W×si−1),当激活函数为tanh时,∂si∂si−1的取值范围为[0, 1]。当激活函数为sigmoid时,∂si∂si−1的取值范围为[0, 1/4](简单的一元函数求导,这里就不展开了)。因为这里我们选择t=3时刻的输出损失,所以连乘的式子的个数并不多。但是我们可以设想一下,对于深度的网络结构而言,若选择tanh或者sigmoid激活函数,对于公式(10)中k取值较小的那一项,一定满足∏3i=k+1∂si∂si−1趋近于0,从而导致了消失梯度问题。
我们再从直观的角度来理解一下消失梯度问题,对于RNN时刻T的输出,其必定是时刻t=1,…,T-1的输入综合作用的结果,也就是说更新模型参数时,要充分利用当前时刻以及之前所有时刻的输入信息。但是如果发生了”消失梯度”问题,就会意味着,距离当前时刻非常远的输入数据,不能为当前模型参数的更新做贡献,所以在RNN的编程实现中,才会有“truncated gradient”这一概念,“截断梯度”就是在更新参数时,只利用较近的时刻的序列信息,把那些“历史悠久的信息”忽略掉了。
解决“消失梯度问题”,我们可以更换激活函数,比如采用Relu(rectified linear units)激活函数,但是更好的办法是使用LSTM或者GRU架构的网络。
LSTM网络
为了解决原始RNN网络结构存在的“vanishing gradient”问题,前辈们设计了LSTM这种新的网络结构。但从本质上来讲,LSTM是一种特殊的循环神经网络,其和RNN的区别在于,对于特定时刻t,隐藏层输出st的计算方式不同。故对LSTM网络的训练的思路与RNN类似,仅前向传播关系式不同而已。值得一提的是,在对LSTM网络进行训练时,cell state c[0]和hidden state s[0]都是随机初始化得到的。
GRU(Gated Recurrent Unit)是2014年提出来的新的RNN架构,它是简化版的LSTM,在超参数(hyper-parameters)均调优的前提下,这两种RNN架构的性能相当,但是GRU架构的参数少,所以需要的训练样本更少,易于训练。LSTM和GRU架构的网络图如下,

关于LSTM网络结构相关的理论,请参见http://colah.github.io/posts/2015-08-Understanding-LSTMs/,相信也只有这样的大牛能把LSTM解析的如此浅显易懂。这里还需要补充说明一下,关于LSTM网络的参数求偏微分,如果我们手动求解的话,也是跟RNN类似的思路,但由于LSTM网络结构比较复杂,手动算的话,式子会变得非常复杂,我们便可以借助深度学习框架的自动微分功能了,现在的框架也都支持自动微分的,比如theano、tensorflow等。
参考资料:http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/
“A tutorial on training recurrent neural networks”. H. Jaeger, 2002.
Recurrent Neural Networks
人类并不是每时每刻都从一片空白的大脑开始他们的思考。在你阅读这篇文章时候,你都是基于自己已经拥有的对先前所见词的理解来推断当前词的真实含义。我们不会将所有的东西都全部丢弃,然后用空白的大脑进行思考。我们的思想拥有持久性。
传统的神经网络并不能做到这点,看起来也像是一种巨大的弊端。例如,假设你希望对电影中的每个时间点的时间类型进行分类。传统的神经网络应该很难来处理这个问题——使用电影中先前的事件推断后续的事件。
RNN 解决了这个问题。RNN 是包含循环的网络,允许信息的持久化。

在上面的示例图中,神经网络的模块,A,正在读取某个输入 x_i,并输出一个值 h_i。循环可以使得信息可以从当前步传递到下一步。
这些循环使得 RNN 看起来非常神秘。然而,如果你仔细想想,这样也不比一个正常的神经网络难于理解。RNN 可以被看做是同一神经网络的多次复制,每个神经网络模块会把消息传递给下一个。所以,如果我们将这个循环展开:

链式的特征揭示了 RNN 本质上是与序列和列表相关的。他们是对于这类数据的最自然的神经网络架构。
并且 RNN 也已经被人们应用了!在过去几年中,应用 RNN 在语音识别,语言建模,翻译,图片描述等问题上已经取得一定成功,并且这个列表还在增长。我建议大家参考 Andrej Karpathy 的博客文章——The Unreasonable Effectiveness of Recurrent Neural Networks 来看看更丰富有趣的 RNN 的成功应用。
而这些成功应用的关键之处就是 LSTM 的使用,这是一种特别的 RNN,比标准的 RNN 在很多的任务上都表现得更好。几乎所有的令人振奋的关于 RNN 的结果都是通过 LSTM 达到的。这篇博文也会就 LSTM 进行展开。
长期依赖(Long-Term Dependencies)问题
RNN 的关键点之一就是他们可以用来连接先前的信息到当前的任务上,例如使用过去的视频段来推测对当前段的理解。如果 RNN 可以做到这个,他们就变得非常有用。但是真的可以么?答案是,还有很多依赖因素。
有时候,我们仅仅需要知道先前的信息来执行当前的任务。例如,我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词,我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中,相关的信息和预测的词位置之间的间隔是非常小的,RNN 可以学会使用先前的信息。

但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France... I speak fluent French”最后的词。当前的信息建议下一个词可能是一种语言的名字,但是如果我们需要弄清楚是什么语言,我们是需要先前提到的离当前位置很远的 France 的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。
不幸的是,在这个间隔不断增大时,RNN 会丧失学习到连接如此远的信息的能力。

在理论上,RNN 绝对可以处理这样的 长期依赖 问题。人们可以仔细挑选参数来解决这类问题中的最初级形式,但在实践中,RNN 肯定不能够成功学习到这些知识。Bengio, et al. (1994)等人对该问题进行了深入的研究,他们发现一些使训练 RNN 变得非常困难的相当根本的原因。
然而,幸运的是,LSTM 并没有这个问题!
LSTM 网络
Long Short Term 网络—— 一般就叫做 LSTM ——是一种 RNN 特殊的类型,可以学习长期依赖信息。LSTM 由Hochreiter & Schmidhuber (1997)提出,并在近期被Alex Graves进行了改良和推广。在很多问题,LSTM 都取得相当巨大的成功,并得到了广泛的使用。
LSTM 通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是 LSTM 的默认行为,而非需要付出很大代价才能获得的能力!
所有 RNN 都具有一种重复神经网络模块的链式的形式。在标准的 RNN 中,这个重复的模块只有一个非常简单的结构,例如一个 tanh 层。

LSTM 同样是这样的结构,但是重复的模块拥有一个不同的结构。不同于 单一神经网络层,这里是有四个,以一种非常特殊的方式进行交互。

不必担心这里的细节。我们会一步一步地剖析 LSTM 解析图。现在,我们先来熟悉一下图中使用的各种元素的图标。

在上面的图例中,每一条黑线传输着一整个向量,从一个节点的输出到其他节点的输入。粉色的圈代表 pointwise 的操作,诸如向量的和,而黄色的矩阵就是学习到的神经网络层。合在一起的线表示向量的连接,分开的线表示内容被复制,然后分发到不同的位置。
LSTM 的核心思想
LSTM 的关键就是细胞状态,水平线在图上方贯穿运行。
细胞状态类似于传送带。直接在整个链上运行,只有一些少量的线性交互。信息在上面流传保持不变会很容易。

LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。

Sigmoid 层输出 0 到 1 之间的数值,描述每个部分有多少量可以通过。0 代表“不许任何量通过”,1 就指“允许任意量通过”!
LSTM 拥有三个门,来保护和控制细胞状态。
逐步理解 LSTM
在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取 h_{t-1} 和 x_t,输出一个在 0 到 1 之间的数值给每个在细胞状态 C_{t-1} 中的数字。1 表示“完全保留”,0 表示“完全舍弃”。
让我们回到语言模型的例子中来基于已经看到的预测下一个词。在这个问题中,细胞状态可能包含当前主语的性别,因此正确的代词可以被选择出来。当我们看到新的主语,我们希望忘记旧的主语。

下一步是确定什么样的新信息被存放在细胞状态中。这里包含两个部分。第一,sigmoid 层称 “输入门层” 决定什么值我们将要更新。然后,一个 tanh 层创建一个新的候选值向量,\tilde{C}_t,会被加入到状态中。下一步,我们会讲这两个信息来产生对状态的更新。
在我们语言模型的例子中,我们希望增加新的主语的性别到细胞状态中,来替代旧的需要忘记的主语。

现在是更新旧细胞状态的时间了,C_{t-1} 更新为 C_t。前面的步骤已经决定了将会做什么,我们现在就是实际去完成。
我们把旧状态与 f_t 相乘,丢弃掉我们确定需要丢弃的信息。接着加上 i_t * \tilde{C}_t。这就是新的候选值,根据我们决定更新每个状态的程度进行变化。
在语言模型的例子中,这就是我们实际根据前面确定的目标,丢弃旧代词的性别信息并添加新的信息的地方。

最终,我们需要确定输出什么值。这个输出将会基于我们的细胞状态,但是也是一个过滤后的版本。首先,我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着,我们把细胞状态通过 tanh 进行处理(得到一个在 -1 到 1 之间的值)并将它和 sigmoid 门的输出相乘,最终我们仅仅会输出我们确定输出的那部分。
在语言模型的例子中,因为他就看到了一个 代词,可能需要输出与一个 动词 相关的信息。例如,可能输出是否代词是单数还是负数,这样如果是动词的话,我们也知道动词需要进行的词形变化。

LSTM 的变体
我们到目前为止都还在介绍正常的 LSTM。但是不是所有的 LSTM 都长成一个样子的。实际上,几乎所有包含 LSTM 的论文都采用了微小的变体。差异非常小,但是也值得拿出来讲一下。
其中一个流形的 LSTM 变体,就是由 Gers & Schmidhuber (2000) 提出的,增加了 “peephole connection”。是说,我们让 门层 也会接受细胞状态的输入。

上面的图例中,我们增加了 peephole 到每个门上,但是许多论文会加入部分的 peephole 而非所有都加。
另一个变体是通过使用 coupled 忘记和输入门。不同于之前是分开确定什么忘记和需要添加什么新的信息,这里是一同做出决定。我们仅仅会当我们将要输入在当前位置时忘记。我们仅仅输入新的值到那些我们已经忘记旧的信息的那些状态 。

另一个改动较大的变体是 Gated Recurrent Unit (GRU),这是由 Cho, et al. (2014) 提出。它将忘记门和输入门合成了一个单一的 更新门。同样还混合了细胞状态和隐藏状态,和其他一些改动。最终的模型比标准的 LSTM 模型要简单,也是非常流行的变体。

这里只是部分流行的 LSTM 变体。当然还有很多其他的,如Yao, et al. (2015) 提出的 Depth Gated RNN。还有用一些完全不同的观点来解决长期依赖的问题,如Koutnik, et al. (2014) 提出的 Clockwork RNN。
要问哪个变体是最好的?其中的差异性真的重要吗?Greff, et al. (2015) 给出了流行变体的比较,结论是他们基本上是一样的。Jozefowicz, et al. (2015) 则在超过 1 万种 RNN 架构上进行了测试,发现一些架构在某些任务上也取得了比 LSTM 更好的结果。

结论
刚开始,我提到通过 RNN 得到重要的结果。本质上所有这些都可以使用 LSTM 完成。对于大多数任务确实展示了更好的性能!
由于 LSTM 一般是通过一系列的方程表示的,使得 LSTM 有一点令人费解。然而本文中一步一步地解释让这种困惑消除了不少。
LSTM 是我们在 RNN 中获得的重要成功。很自然地,我们也会考虑:哪里会有更加重大的突破呢?在研究人员间普遍的观点是:“Yes! 下一步已经有了——那就是注意力!” 这个想法是让 RNN 的每一步都从更加大的信息集中挑选信息。例如,如果你使用 RNN 来产生一个图片的描述,可能会选择图片的一个部分,根据这部分信息来产生输出的词。实际上,Xu, et al.(2015)已经这么做了——如果你希望深入探索注意力可能这就是一个有趣的起点!还有一些使用注意力的相当振奋人心的研究成果,看起来有更多的东西亟待探索……
注意力也不是 RNN 研究领域中唯一的发展方向。例如,Kalchbrenner, et al. (2015) 提出的 Grid LSTM 看起来也是很有前途。使用生成模型的 RNN,诸如Gregor, et al.(2015) Chung, et al. (2015) 和 Bayer & Osendorfer (2015) 提出的模型同样很有趣。在过去几年中,RNN 的研究已经相当的燃,而研究成果当然也会更加丰富!
LSTM里面为什么用到Sigmoid和tanh函数
The related question, "Why are sigmoids used in LSTMs where they are?" is also answered based on the possible outputs of the function: "gating" is achieved by multiplying by a number between zero and one, and that's what sigmoids output.
There aren't really meaningful differences between the derivatives of sigmoid and tanh; tanh is just a rescaled and shifted sigmoid: see Richard Socher's Neural Tips and Tricks. If second derivatives are relevant, I'd like to know how.
LSTM及其变种及其克服梯度消失的更多相关文章
- 讨论LSTM和RNN梯度消失问题
1RNN为什么会有梯度消失问题 (1)沿时间反向方向:t-n时刻梯度=t时刻梯度* π(W*激活函数的导数)
- LSTM如何解决梯度消失或爆炸的?
from:https://zhuanlan.zhihu.com/p/44163528 哪些问题? 梯度消失会导致我们的神经网络中前面层的网络权重无法得到更新,也就停止了学习. 梯度爆炸会使得学习不稳定 ...
- RNN梯度消失和爆炸的原因 以及 LSTM如何解决梯度消失问题
RNN梯度消失和爆炸的原因 经典的RNN结构如下图所示: 假设我们的时间序列只有三段, 为给定值,神经元没有激活函数,则RNN最简单的前向传播过程如下: 假设在t=3时刻,损失函数为 . 则对于一 ...
- Recurrent Neural Network系列3--理解RNN的BPTT算法和梯度消失
作者:zhbzz2007 出处:http://www.cnblogs.com/zhbzz2007 欢迎转载,也请保留这段声明.谢谢! 这是RNN教程的第三部分. 在前面的教程中,我们从头实现了一个循环 ...
- 机器学习 —— 基础整理(八)循环神经网络的BPTT算法步骤整理;梯度消失与梯度爆炸
网上有很多Simple RNN的BPTT(Backpropagation through time,随时间反向传播)算法推导.下面用自己的记号整理一下. 我之前有个习惯是用下标表示样本序号,这里不能再 ...
- bp算法中为什么会产生梯度消失?
作者:维吉特伯链接:https://www.zhihu.com/question/49812013/answer/148825073来源:知乎著作权归作者所有.商业转载请联系作者获得授权,非商业转载请 ...
- 梯度消失&&梯度爆炸
转载自: https://blog.csdn.net/qq_25737169/article/details/78847691 前言 本文主要深入介绍深度学习中的梯度消失和梯度爆炸的问题以及解决方案. ...
- Backpropagation Through Time (BPTT) 梯度消失与梯度爆炸
Backpropagation Through Time (BPTT) 梯度消失与梯度爆炸 下面的图显示的是RNN的结果以及数据前向流动方向 假设有 \[ \begin{split} h_t & ...
- [ DLPytorch ] 循环神经网络进阶&拟合问题&梯度消失与爆炸
循环神经网络进阶 BPTT 反向传播过程中,训练模型通常需要模型参数的梯度. \[ \frac{\partial L}{\partial \boldsymbol{W}_{qh}} = \sum_{t= ...
随机推荐
- 数百种编程语言,而我为什么要学 Python?
是应用率最高.长期霸占排行榜的常青藤 Java?是易于上手,难以精通的 C?还是在游戏和工具领域仍占主流地位的 C++?亦或是占据 Windows 桌面应用程序半壁江山的 C#?…… 我想,每个人可能 ...
- 《Java程序设计》第8周学习总结 20165218 2017-2018-1
20165218 2017-2018-1 <Java程序设计>第8周学习总结 教材学习内容总结 第12章 java多线程机制 java中的线程 计算机在任何给定时刻只能执行一个线程,多线程 ...
- Codeforces Round #301 (Div. 2)A B C D 水 模拟 bfs 概率dp
A. Combination Lock time limit per test 2 seconds memory limit per test 256 megabytes input standard ...
- 洛谷P1637 三元上升子序列
P1637 三元上升子序列 48通过 225提交 题目提供者该用户不存在 标签云端 难度提高+/省选- 时空限制1s / 128MB 提交 讨论 题解 最新讨论更多讨论 为什么超时啊 a的数据比较 ...
- 对于redis底层框架的理解(五)
之前总结了redis的通讯流程,基本框架,epoll的封装等等,这次介绍下 redis对于select模型的封装 //select 模型 typedef struct aeApiState { //读 ...
- RabbitMQ的基础介绍
转自:http://blog.csdn.net/whycold/article/details/41119807 一.引言 你是否遇到过两个(多个)系统间需要通过定时任务来同步某些数据?你是否在为异构 ...
- JS事件大全及兼容
一般事件 事件 浏览器支持 描述 onClick IE3|N2|O3 鼠标点击事件,多用在某个对象控制的范围内的鼠标点击 onDblClick IE4|N4|O 鼠标双击事件 onMouseDown ...
- 2017北京国庆刷题Day7 afternoon
期望得分:100+30+100=230 实际得分:60+30+100=190 排序去重 固定右端点,左端点单调不减 考场上用了二分,没去重,60 #include<cstdio> #inc ...
- CF540 B 贪心
坑在B题是常态,弱智的日常. 是找中位数不是平均值. 慌了,乱写了 出了一塌糊涂的ZZ代码 特记一下 /** @Date : 2017-08-27 17:25:11 * @FileName: B.cp ...
- 817C. Really Big Numbers 二分
LINK 题意:给出两个数n, s,要求问1~n中\(x-bit(x)>=s\)的数有多少个.其中bit(x)指x的各位数之和 思路:首先观察能够发现,对于一个数如果满足了条件,由于x-bit( ...
