Tarjan 模板，高级并查集

第一个模板有误！！！！

请见谅！！！

要怪就怪HDU吧，竟然让我过了

第二个模板是正确的。请翻到下面看更新

HDU 1269

评论区居然有人说用并查集过了，其实回想一下

求无向图的连通分量，就是并查集，求有向图的话，就要用到这个算法，或者Kosaraju。

再回想一下，Tarjan确实比较像并查集，我在第一次写的时候就有这种感觉

请看：

这是我在找强连通分量的数量，而在并查集里面，就是：

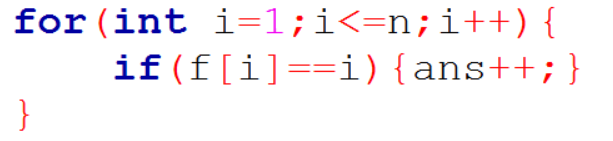
这样看来，其实，low的含义就是这个f[i],而由于有向图有其顺序的，所以用num[i]记录其访问的顺序。。。。。

无论是代码，还是算法，Tarjan都像极了并查集，不得不说，Trajan其实就是一个高级并查集算法

下面贴下我的模板，这个模板只是过了HDU 1269，看discuss数据比较水，不是太敢确定模板的正确性

说明：num记录访问的顺序，book记录是否访问过，low--按并查集的说法，就是更新它的爸爸，直到它的祖宗（想一下整个算法，确实如此）

有机会看一下这个吧，他写的蛮好的，我就是看了这个才看懂

https://blog.csdn.net/mengxiang000000/article/details/51672725

 #include<iostream>
 #include<vector>
 #include<cstring>
 using namespace std;
 vector<int>u[];
 bool book[];
 int index;
 int num[],low[];
 void Tarjan_dfs(int t)
 {
     index++;book[t]=true;
     low[t]=num[t]=index;
     for(int i=;i<u[t].size();i++){
         if(!book[u[t][i]]){
             Tarjan_dfs(u[t][i]);
         }
         low[t]=min(low[t],low[u[t][i]]);
     }
 }

 int main()
 {
     int n,m;
     while(cin>>n>>m&&n&&m){
         int x,y;
         index=;
         memset(book,,sizeof(book));
         for(int i=;i<m;i++){
             cin>>x>>y;
             u[x].push_back(y);
         }
         for(int i=;i<=n;i++){
             if(!book[i]){Tarjan_dfs(i);}
         }
         int ans=;
         for(int i=;i<=n;i++){
             if(low[i]==num[i]){ans++;}
         }
         for(int i=;i<=n;i++){
             printf("%d %d\n",num[i],low[i]);
         }
         cout<<ans<<endl;
     }
     return ;
 }

　　——————————————————————————————————————————————————————————————————

实在抱歉，居然搞了一个错误的模板。

由于模板的错误，之前的理解也有些偏差，其实和并查集相似的不是low，而是color。

接下来是我的板子，这是POJ2553的代码，只有solve函数与此题有关。

#include<iostream>
#include<cstdio>
#include<vector>
#include<stack>
#include<cstring>
using namespace std;
int n,m;
int book[50008];
int low[50008],num[50008],cnt=1,index;
int color[50008];
bool flag[50008];
vector<int>u[50008];
stack<int>st;
int sig=0;
void Tarjan(int t)
{
    num[t]=low[t]=++index;
    st.push(t);
    book[t]=true;
    int siz=u[t].size();
    for(int i=0;i<siz;i++){
        if(!num[u[t][i]]){
            Tarjan(u[t][i]);
            low[t]=min(low[t],low[u[t][i]]);
        }
        else if(book[u[t][i]]){low[t]=min(low[t],low[u[t][i]]);}
    }

    if(num[t]==low[t]){
        sig++;
        while(1){

            cnt=st.top();
            st.pop();
            color[cnt]=sig;
            book[cnt]=0;
            if(cnt==t){break;}
        }
    }
}

bool init()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        u[i].clear();
    }
    while(!st.empty()){
        st.pop();
    }
    memset(book,0,sizeof(book));
    memset(low,0,sizeof(low));
    memset(flag,0,sizeof(flag));
    memset(color,0,sizeof(color));
    memset(num,0,sizeof(num));
    index=0;
    if(n==0){return false;}
    scanf("%d",&m);
    int x,y;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        u[x].push_back(y);
    }
    return true;
}

void solve()
{
    int siz;
    int tle=0;
    for(int i=1;i<=n;i++){
        siz=u[i].size();
        for(int j=0;j<siz;j++){
            if(color[u[i][j]]!=color[i]){flag[color[i]]=true;}
        }
    }

    for(int i=1;i<=n;i++){
        if(!flag[color[i]]){
            tle++?printf(" %d",i):printf("%d",i);
        }
    }
    printf("\n");
}

int main()
{
    while(init()){
        for(int i=1;i<=n;i++){
            if(!num[i]){Tarjan(i);cnt++;}
        }
        solve();
    }
}