算法入门及其C++实现

https://github.com/yuwei67/Play-with-Algorithms

(nlogn)为最优排序算法

选择排序

整个数组中，先选出最小元素的位置，将该位置与当前的第一位交换；然后选出剩下数组中，最小元素的位置，将此元素与第二位元素交换；以此类推

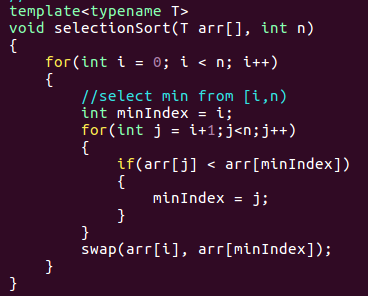
srand和rand函数使用前，需要包含 stdlib.h和time.h；

插入排序

类似于玩扑克牌时的思想，看后面牌中的每一张牌，然后插入到前方合适的位置

单独看8，不需要排序

6与前面的8比，6小于8，于是6和8互换位置

2先和8比，2小于8，于是互换位置

接下来2和6比，2小于6，于是互换位置，至此前三个数排序结束，后面的排序同理。

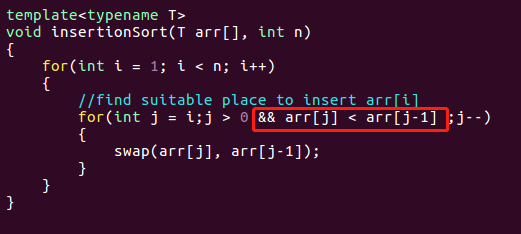
相较于选择排序，不需要每次遍历所有内容，有提前终止机会，当数组近乎有序时，插入排序效率远高于选择排序，甚至比很多O(nlogn)级别排序算法效率高；

优化插入排序：不贸然交换位置，思路如下

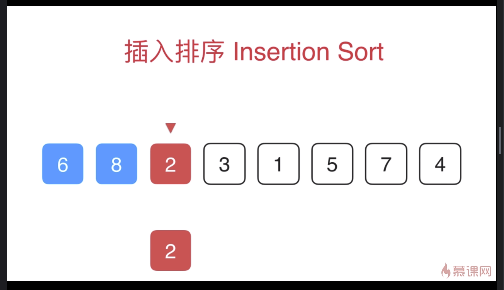
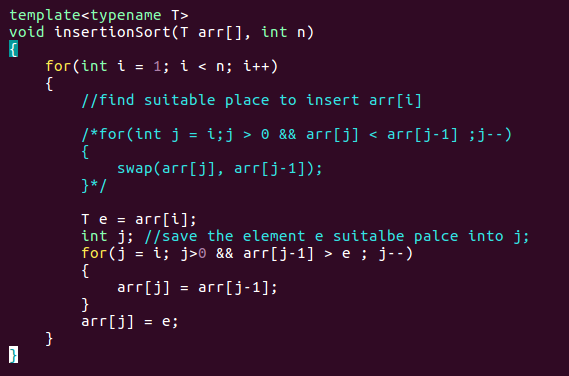
当考察 “2” 时，先把2这个元素复制一个副本，看是否应该放在这个位置，发现2比前面的8小，所以不应该放在这儿，那么将此位置的值赋值为8，然后考察2是不是应该放在原来8的位置；2比这个位置的前一个位置的6要小，所以6放到这个位置；之后看2是不是应该放在原来6的位置，由于是第0个位置，所以2应该放在此处，至此，对2的排序结束。

一次swap是3次赋值，优化后变为多次比较后1次赋值

插入排序，对近乎有序的数组，可以降到O(N)的复杂度

归并排序（自顶向下，使用递归）

将数组对半分成2份，左右分别单独排序，本质是递归排序的过程。

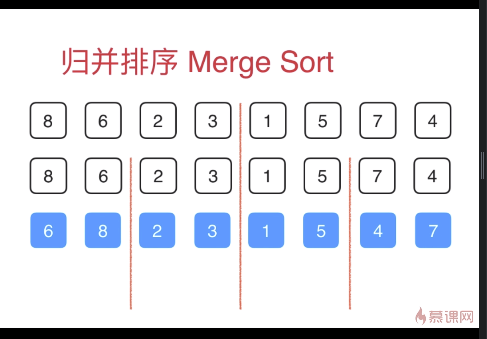
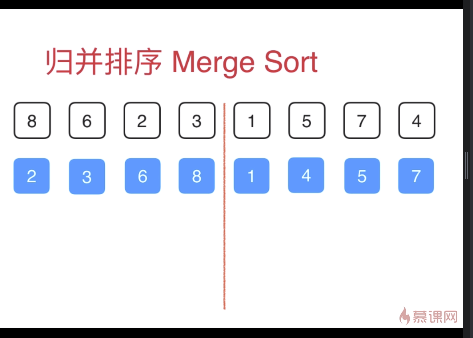
时间复杂度比O(N^2)小，但是需要开辟辅助空间

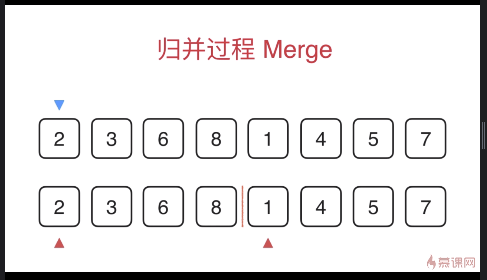
1比2小，所以1放在蓝色指针当前位置，蓝色指针后移，辅助空间中1对应的红色指针后移

之后比较2和4，具体过程同前一步，以此类推。

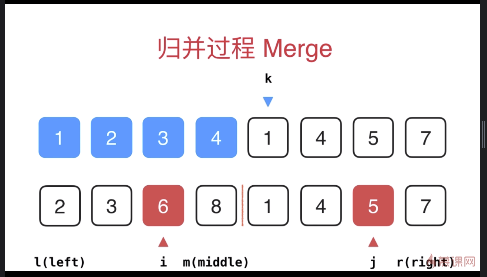
具体实现：i 和 j 表示当前正在考虑的元素，k 指向这两个元素相比较之后，最终应该放到归并数组中的位置（是下一个需要放置的位置，不是已经排好序的最后一位）

代码示例（未优化，对近乎有序数组性能较差）：

 // 将arr[l...mid]和arr[mid+1...r]两部分进行归并
 template<typename  T>
 void __merge(T arr[], int l, int mid, int r){

     // 经测试,传递aux数组的性能效果并不好
     T aux[r-l+];
     for( int i = l ; i <= r; i ++ )
         aux[i-l] = arr[i];

     int i = l, j = mid+;
     for( int k = l ; k <= r; k ++ ){

         if( i > mid )   { arr[k] = aux[j-l]; j ++;}
         else if( j > r ){ arr[k] = aux[i-l]; i ++;}
         else if( aux[i-l] < aux[j-l] ){ arr[k] = aux[i-l]; i ++;}
         else                          { arr[k] = aux[j-l]; j ++;}
     }
 }

 // 递归使用归并排序,对arr[l...r]的范围进行排序
 template<typename T>
 void __mergeSort(T arr[], int l, int r){

     if( l >= r )
         return;

     int mid = (l+r)/;
     __mergeSort(arr, l, mid);
     __mergeSort(arr, mid+, r);
     __merge(arr, l, mid, r);
 }

 template<typename T>
 void mergeSort(T arr[], int n){

     __mergeSort( arr ,  , n- );
 }

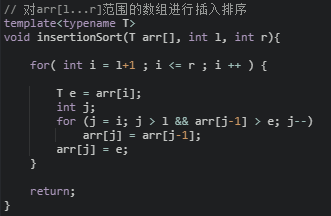
代码优化（第一次）

20 // 递归使用归并排序,对arr[l...r]的范围进行排序
21 template<typename T>
22 void __mergeSort(T arr[], int l, int r){
23 
　　　　//对所有条件的优化（小数组使用插入排序，一是因为此时数组近乎有序的概率会比较大，
　　　　//二是因为 N^2 和 NlogN 前是有常数的系数的，对于这个系数，插入排序比归并排序小，所以当N小到一定程度时，插入排序会比归并排序快一些）
　　　　//15这个数是最优的么？
24     //if( l >= r )
25     //    return;
　　　　if( r - l <= 15)
　　　　{
　　　　　　insertionSort(arr,l,r);
　　　　}
26
27     int mid = (l+r)/2;
28     __mergeSort(arr, l, mid);
29     __mergeSort(arr, mid+1, r);
　　　　//对近乎有序数组的优化
　　　　if(arr[mid] > arr[mid+1])
30     　　__merge(arr, l, mid, r);
31 }

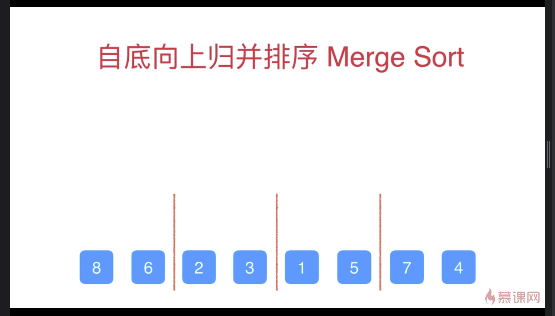
归并排序（自底向上，使用迭代，统计意义上效率稍弱于递归方式实现）

由于没有使用索引直接获取元素，可以非常好的使用NlogN的时间对链表这样的数据结构进行排序

快速排序

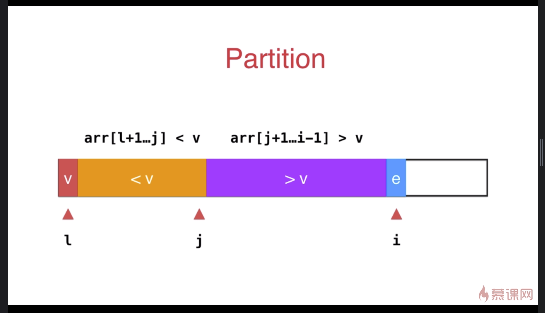
思路：每次从当前数组中选择一个元素，将这个元素想办法挪到排好序的数组中应该在的位置，那么以这个元素为基点，前面的数比他小，后面的数比他大。

　　　　之后对前后两个数组分别继续使用快速排序。

子过程如下：如果当前访问的元素 e 比 v 大，i 指针直接后移；否则调换 i 和 j 后面元素的位置，j 指针后移, i 指针后移；遍历完成后，交换 l 和 j 元素的位置。

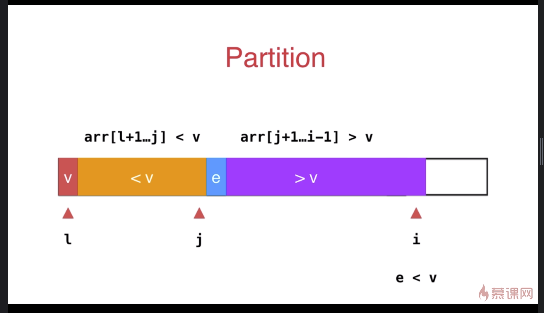
 // 对arr[l...r]部分进行partition操作
 // 返回p,使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
 template <typename T>
 int __partition(T arr[], int l, int r){

     T v = arr[l];

     int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
     for( int i = l +  ; i <= r ; i ++ )
         if( arr[i] < v ){
             j ++;
             swap( arr[j] , arr[i] );
         }

     swap( arr[l] , arr[j]);

     return j;
 }

 // 对arr[l...r]部分进行快速排序
 template <typename T>
 void __quickSort(T arr[], int l, int r){

     if( l >= r )
         return;

     int p = __partition(arr, l, r);
     __quickSort(arr, l, p- );
     __quickSort(arr, p+, r);
 }

 template <typename T>
 void quickSort(T arr[], int n){

     __quickSort(arr, , n-);
 }

快速排序优化（针对近乎有序数组）

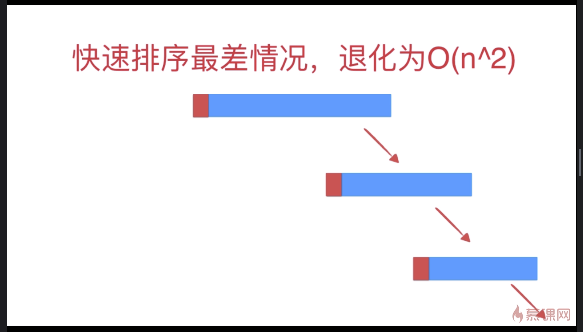
 template <typename T>
 int _partition(T arr[], int l, int r){

     swap( arr[l] , arr[rand()%(r-l+)+l] );

     T v = arr[l];
     int j = l;
     for( int i = l +  ; i <= r ; i ++ )
         if( arr[i] < v ){
             j ++;
             swap( arr[j] , arr[i] );
         }

     swap( arr[l] , arr[j]);

     return j;
 }

 template <typename T>
 void _quickSort(T arr[], int l, int r){

 //    if( l >= r )
 //        return;
     if( r - l <=  ){
         insertionSort(arr,l,r);
         return;
     }

     int p = _partition(arr, l, r);
     _quickSort(arr, l, p- );
     _quickSort(arr, p+, r);
 }

 template <typename T>
 void quickSort(T arr[], int n){

     srand(time(NULL));
     _quickSort(arr, , n-);
 }

快速排序优化（双路快速排序法，针对大量重复元素的数组）

之前小于 v 和大于 v 的数组放于数组的一段，优化后放于数组的两端

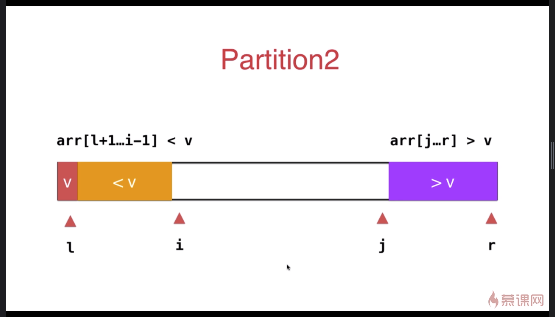
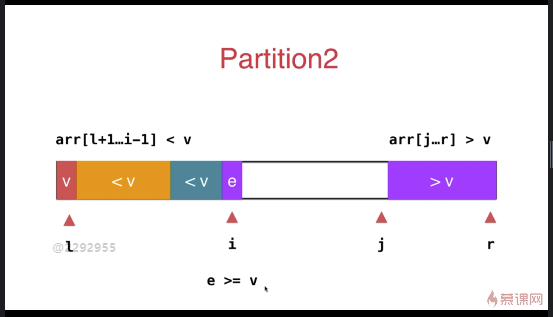
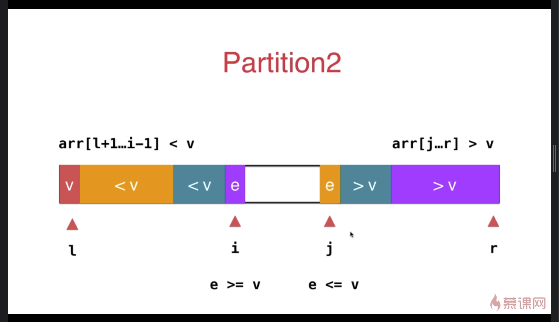
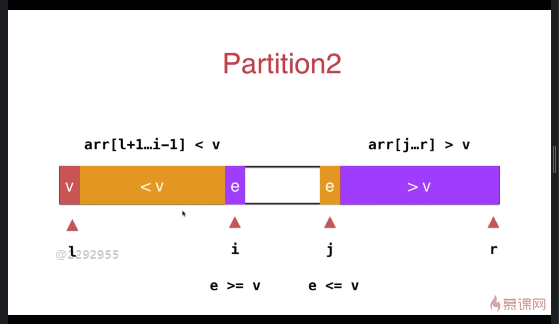
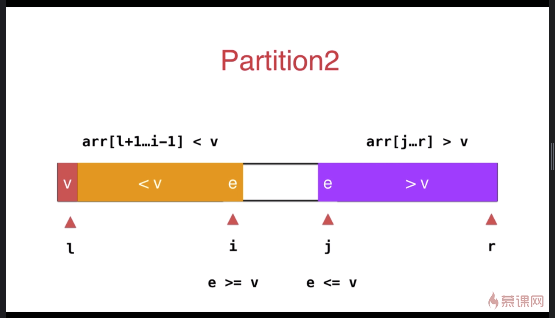
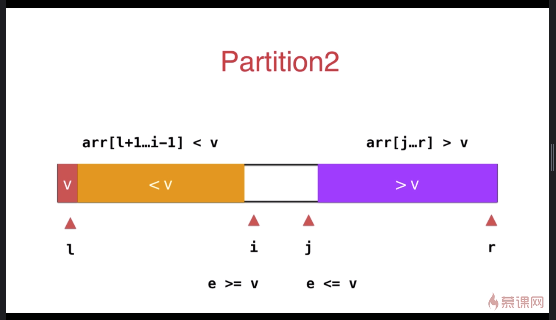
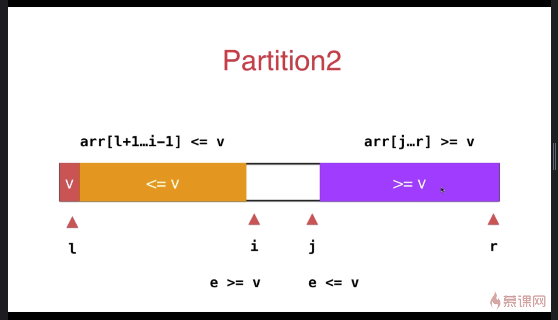
与之前的partition相比较，此方式的最大特点是将等于 v 的元素分散到两侧，不会出现大量相同元素集中在一侧的情况

 template <typename T>
 int _partition2(T arr[], int l, int r){

     swap( arr[l] , arr[rand()%(r-l+)+l] );
     T v = arr[l];

     // arr[l+1...i) <= v; arr(j...r] >= v
     int i = l+, j = r;
     while( true ){
         while( i <= r && arr[i] < v )
             i ++;

         while( j >= l+ && arr[j] > v )
             j --;

         if( i > j )
             break;

         swap( arr[i] , arr[j] );
         i ++;
         j --;
     }

     swap( arr[l] , arr[j]);

     return j;
 }

 template <typename T>
 void _quickSort(T arr[], int l, int r){

 //    if( l >= r )
 //        return;
     if( r - l <=  ){
         insertionSort(arr,l,r);
         return;
     }

     int p = _partition2(arr, l, r);
     _quickSort(arr, l, p- );
     _quickSort(arr, p+, r);
 }

三路快速排序

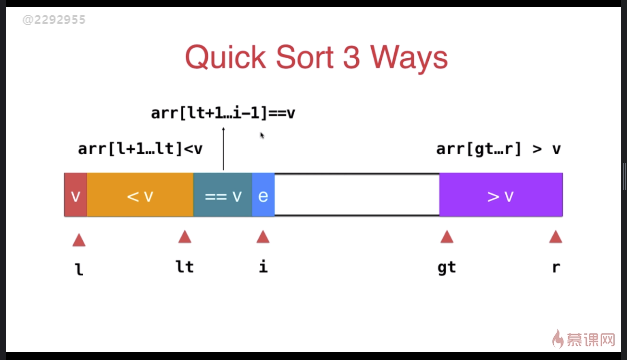
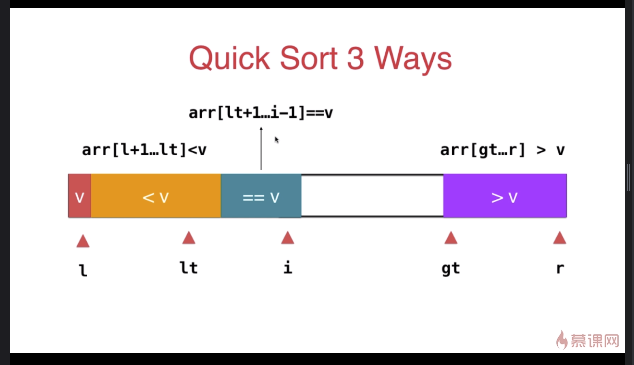
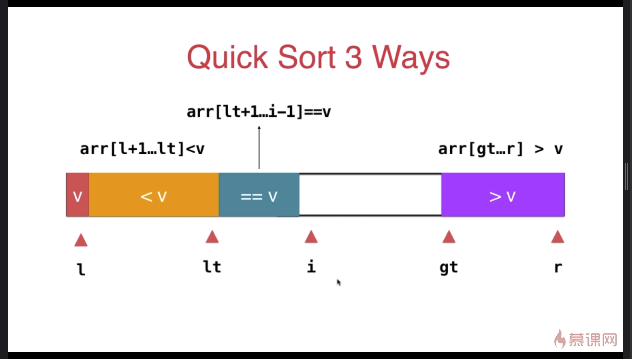
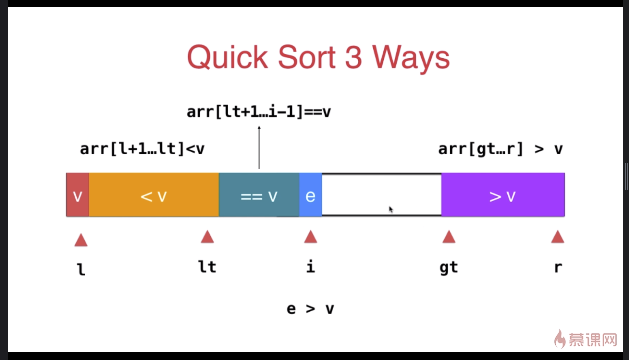
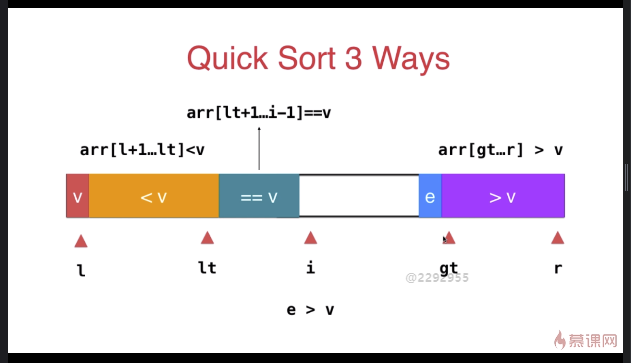
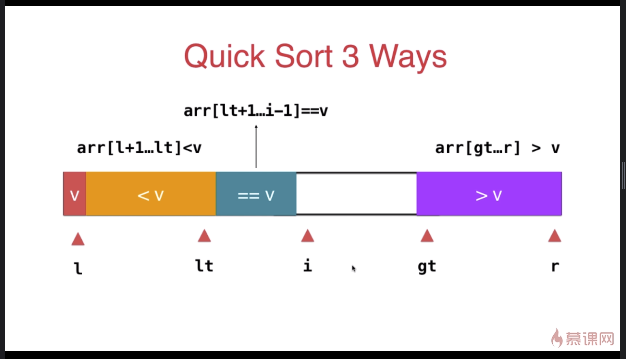
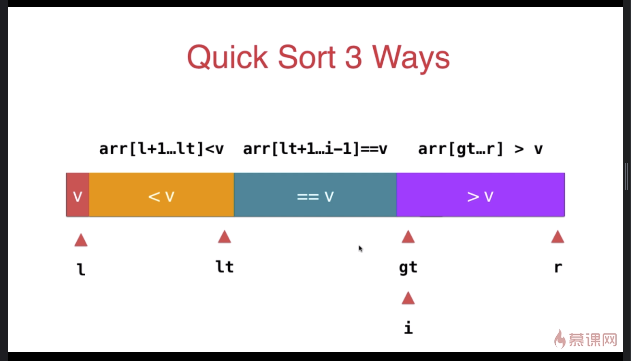
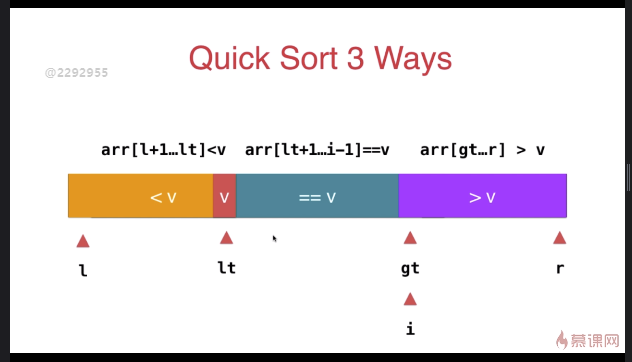
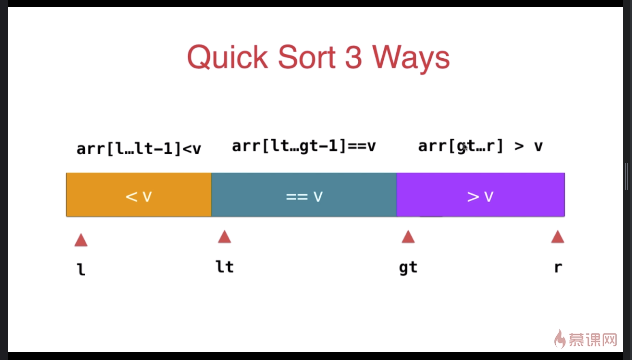
 template <typename T>
 void __quickSort3Ways(T arr[], int l, int r){

     if( r - l <=  ){
         insertionSort(arr,l,r);
         return;
     }

     swap( arr[l], arr[rand()%(r-l+)+l ] );

     T v = arr[l];

     int lt = l;     // arr[l+1...lt] < v
     int gt = r + ; // arr[gt...r] > v
     int i = l+;    // arr[lt+1...i) == v
     while( i < gt ){
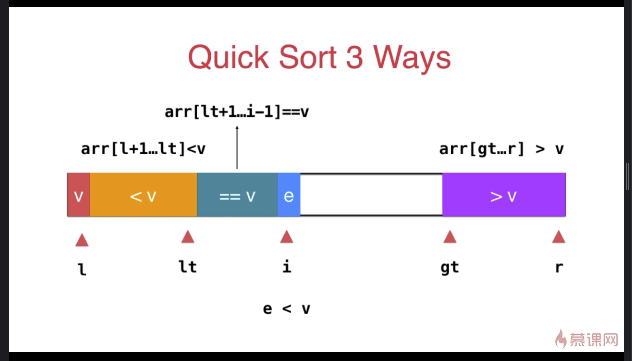
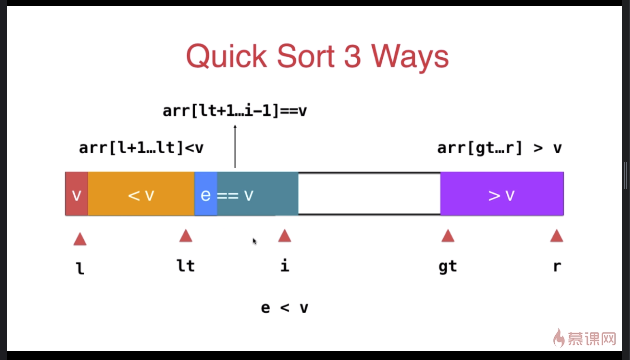
         if( arr[i] < v ){
             swap( arr[i], arr[lt+]);
             i ++;
             lt ++;
         }
         else if( arr[i] > v ){
             swap( arr[i], arr[gt-]);
             gt --;
         }
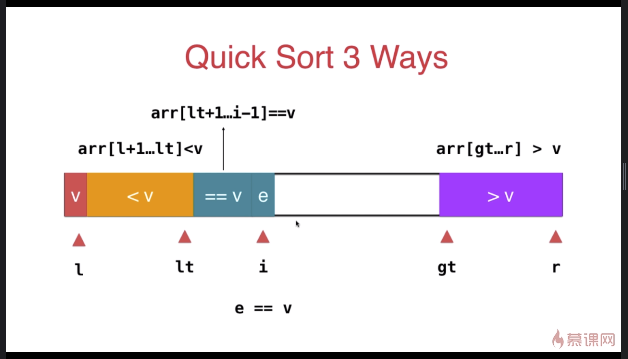
         else{ // arr[i] == v
             i ++;
         }
     }

     swap( arr[l] , arr[lt] );

     __quickSort3Ways(arr, l, lt-);
     __quickSort3Ways(arr, gt, r);
 }

 template <typename T>
 void quickSort3Ways(T arr[], int n){

     srand(time(NULL));
     __quickSort3Ways( arr, , n-);
 }