1.修改器列表：

将常用的修改器放放置在集里：

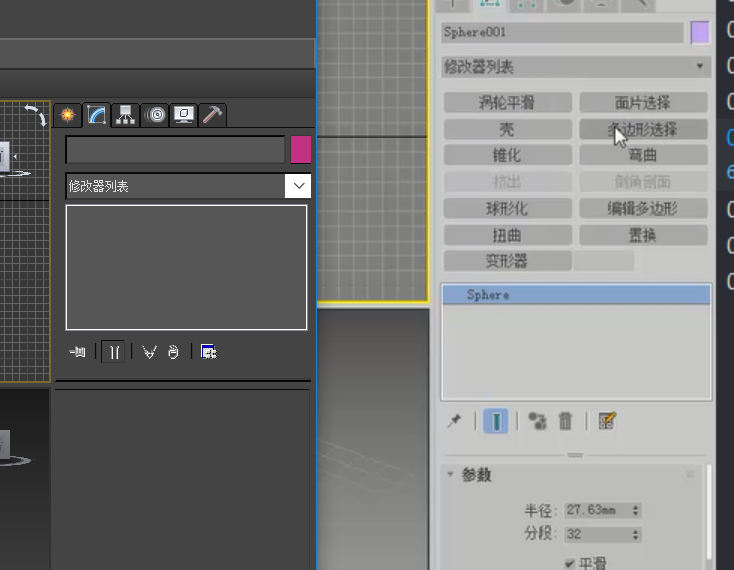
1.点击【配置】按钮，勾选【显示按钮】

选择【配置修改器集】，在新出的弹窗里通过左右拖拽进行设置；

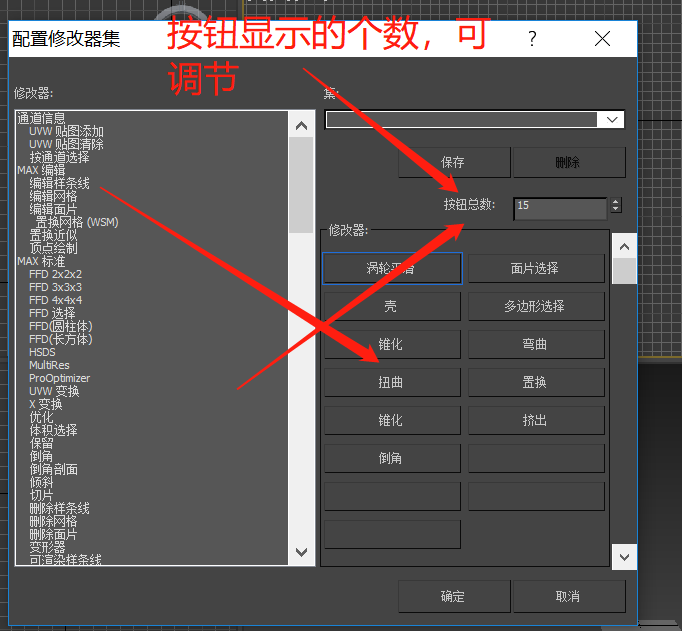
2，选择之后，点击【确定】进行保存；

3ds max学习笔记（十一）-- 修改器的更多相关文章

  1. 3ds max学习笔记（六）-- 基本操作（建模前奏）

    1.界面设置 在3ds Max的版本的界面中,默认是较深.若需要切换至较亮的界面,步骤: 执行“自定义”菜单,选择“加载自定义用户界面方案”从弹出的界面中选择样式文件,单击“打开”即可: 注:“amg ...

  2. 3ds max学习笔记（十五）-- 二维图形的操作

    (二维图形的创建) 1,在命令面板的[新建],单击第二个按钮: 从中选择对象名称,在视图种单击拖动进行创建,特殊:线:摁[shift]限制水平,垂直方向: 2,二维对象参数: 在渲染中启用:显示二维线 ...

  3. 3ds max学习笔记（十三）-- （锥化，扭曲,晶格）

    锥化: 新建一个长方体,在修改器列表中选择--锥化: 参数同弯曲有些类似 参数里: 数量:控制上界面的缩放 曲线:橘黄色的线(但模型未发生变化,此时,可以回到物体身上,调整对应方向上的分段数) 组(有 ...

  4. 3ds max学习笔记（十二）-- （弯曲：实例旋转楼梯）

    一般来讲,弯曲以不扭曲为原则: 新建一个圆柱体,在修改器列表中点击[弯曲]即可: 参数如下: 角度的正负表示的是方向的不同, 方向基本不更改,若要更改则90,-90: 限制:物体(或组)哪些受弯曲的影 ...

  5. mongodb 学习笔记 2 --- 修改器

    修改器是为了爱update文档时,不需要传入整个文档就能修改当前文档的某个属性值,修改器用法如下: 假设数据库中foo集合中存在如下文档:{"name":"jack&qu ...

  6. 3ds max 学习笔记（四）--创建物体

    添加物体: 1.初创建物体,从单视图进行创建,便于处于同一平面,在透视图观看效果.2.在基本对象处选择“长方体”:左键开始制作,松开左键此时控制的是长方形的高,然后点击左键完成:注:在max里点击右键 ...

  7. 3ds max学习笔记-- 复合对象运算

    1,ProBoolean(超级布尔) 栗子: 新建一长方体,两个圆柱体,如下: 选择底部长方体,进入[复合对象],修改[操作],单击[拾取操作对象B],点击圆柱: 效果如下,线面较多: 高级布尔效果图 ...

  8. 3ds max学习笔记（十）-- 实例操作(镜像和对齐)

    1,镜像 选择物体对象然后点击: 偏移:新对象距离轴心所在的直线的距离: 2.对齐 栗子: 选择小球,点击[对齐];鼠标放置在图种位置,点击鼠标左键 出现弹框 调整位置: 先选择对齐位置-->当 ...

  9. 3ds max学习笔记（九）-- 实例操作(路径阵列)

    栅栏 路径阵列也叫间隔工具,将选择的物体沿指定的路径进行复制.实现物体在路径上的饿均匀分布. 选择需要分布的物体对象,在视图中绘制二维图形做为路径线条. 1.选择线条,制作路径 2.选择需要分布的物体 ...

随机推荐

  1. JCenter下载太慢, jcenter修改 https为http也许能帮助你

    今天导入一个工程到studio,一直卡在下载那块. 看到下载地址是:https://jcenter.bintray.com/........https!!!! 到浏览器下载,果然也下载不下来.. 于是 ...

  2. [LeetCode] Best Time to Buy and Sell Stock 6道合集【DP】

    1. Best Time to Buy and Sell Stock 2. Best Time to Buy and Sell Stock II 3. Best Time to Buy and Sel ...

  3. Linux-GLIBCXX版本过低导致编译错误--version `GLIBCXX_3.4.20' not found

    最近在CentOS6.2上安装protobuf2.4.1,编译的时候出现如下错误: /usr/lib64/libstdc++.so.6: version `GLIBCXX_3.4.20' not fo ...

  4. seafile+glusterfs 安装部署

    今天在虚拟机上搭一下seafile,用于测试环境.此处安装的是社区免费版本的,可以使用一键自动安装(MySQL适用). 官方文档:https://manual-cn.seafile.com/ 1.一键 ...

  5. Codeforces 868F Yet Another Minimization Problem 决策单调性 (看题解)

    Yet Another Minimization Problem dp方程我们很容易能得出, f[ i ] = min(g[ j ] + w( j + 1, i )). 然后感觉就根本不能优化. 然后 ...

  6. JQ JS复制到剪贴板

    示例: <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8 ...

  7. BZOJ2120 数颜色 莫队 带修莫队

    原文链接https://www.cnblogs.com/zhouzhendong/p/BZOJ2120.html 题目传送门 - BZOJ2120 题意 给定一个长度为 $n$ 的序列 $a$ ,有 ...

  8. 用jquery设置的值，miniui.getData取不到

    用jquery设置的值,miniui.getData取不到

  9. Scala-Unit4-Scala数组/集合

    一.Scala数组 1.数组的定义: 方法一:val arr = new Array[String](3) String代表数据的元素类型.3表示数组的长度 方法二:val arr = Array[I ...

  10. STRING DELIMITED BY SIZE

    The following COBOL program depicts the use of  STRING DELIMITED BY SIZE                 IDENTIFICAT ...