BZOJ.4558.[JLOI2016]方(计数 容斥)

BZOJ

洛谷

图基本来自这儿。

看到这种计数问题考虑容斥。\(Ans=\) 没有限制的正方形个数 - 以\(i\)为顶点的正方形个数 + 以\(i,j\)为顶点的正方形个数 - 以\(i,j,k\)为顶点的正方形个数 + 以\(i,j,k,l\)为顶点的正方形个数，\(i,j,k,l\)都代表不同的坏点。

其实说，\(Ans=\) 至少包含\(0\)个坏点的正方形个数 - 至少包含\(1\)个坏点的正方形个数 + 至少包含\(2\)个的个数 - 至少包含\(3\)个的个数 + 至少包含\(4\)个的个数，更好想吧，但注意虽说是正方形个数，同一个位置的正方形是可以被重复统计的。

没有限制的正方形个数，问题在于斜着的正方形有多少个。我们发现每个斜着的正方形都可以被最小的完全包含它的正方形所确定，比如：



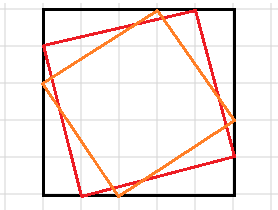
这样每个边长为\(i\)的正方形内部都有\(i-1\)个正方形，算上它自己也就是\(i\)个正方形。

所以总的正方形个数就是\(\sum_{i=1}^{\min(n,m)}(n-i+1)*(m-i+1)*i\)，可以\(O(n)\)计算。

然后是有\(1\)个坏点作为顶点的正方形个数。同样难在如何计算斜着的正方形。

因为如果一个点在一个正着的正方形的边上，那么就可以唯一确定以这个点为顶点的一个斜着的正方形。如图：



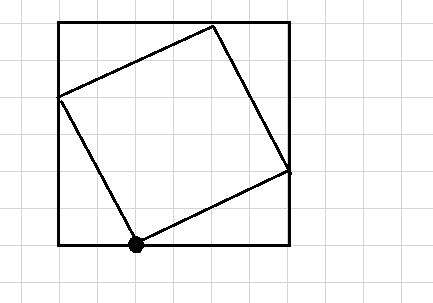
也就是只要它在一个正方形的边上，就可以唯一确定一个斜着的正方形，只需要算这个点在多少个正方形的边上就可以了。

一个点在正方形上边那条边上，和在下边/左边/右边那条边上算起来应该都是差不多的。

所以考虑它在多少个正方形的下边那条边上（朝上的正方形有多少个）。

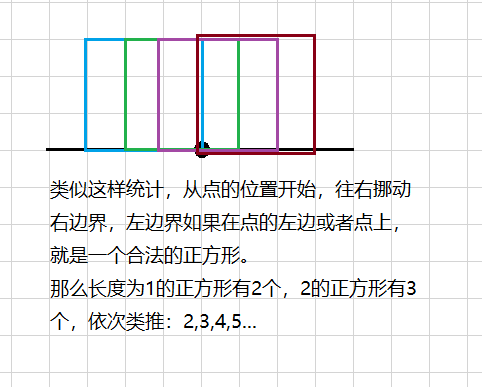
如图，先不考虑上边界及左右边界限制，有\(i+1\)个长度为\(i\)的正方形的下边包含它。

记\(h,l,r\)分别表示当前点到上/左/右边界的距离，长度的限制就是不超过\(t=\min(l+r,h)\)。那么此时的答案就是\(2+3+4+...+t+1=\frac{t(t+3)}{2}\)。

显然直接这么算出来的正方形是可能超过左右边界的。如图，底下的黑色是边界：



不难看出如果\(t\)超过\(l\)，那么超过左边界的正方形有\(1+2+3+...+(t-l)=\frac{(t-l)(t-l+1)}{2}\)个，减掉就可以了。右边界的处理一样。

这样朝上的正方形有多少个就处理完了。朝下/左/右的正方形个数计算同理，把\(h,l,r\)换一下就可以了。

这时我们发现有些正方形会被计算两次，如图中橙色的：



显然这种正方形是完全位于当前点左上方向的，有多少个就算一下到左上边界的距离，减掉就可以了。

这样以至少一个坏点为顶点的正方形就处理完了。复杂度只有\(O(k)\)。

对于以两个坏点为顶点的正方形，显然枚举这两个坏点后就基本确定这个正方形的位置了。

只有以下三种可能且另外两点的坐标可以直接求出：（图来自\(cmd2001\)题解）



黄色的正方形可能顶点直接不在网格上。判一下。

然后求出另外两点，判一下是否越界就可以了。

对于以三/四个坏点为顶点的正方形，在刚刚枚举两个的时候我们已经确定正方形的四个点了，只需要判断确定的这个正方形是否有三/四个坏点就可以了（另外两个点是否也是坏点）。

显然这样对于三个的会重复统计\(C_3^2\)次，对于四个的会重复统计\(C_4^2\)次。除掉就行了。

所以这部分复杂度\(O(k^2\log k)\)或\(O(k^2)\)，看你用什么判坏点。

OK，做完啦。

//39924kb	2744ms
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define mod 100000007
#define Legal(x,y) (x>=0&&x<=n&&y>=0&&y<=m)
typedef long long LL;
const int N=2005;

int n,m,t2,t3,t4;
struct Hash_Table
{
	#define Sz 10000000
	int Enum,H[Sz+2],nxt[N]; LL to[N];
	inline void Insert(int x,int y)
	{
		LL v=1ll*x*1000001+y; x=v%Sz;
		to[++Enum]=v, nxt[Enum]=H[x], H[x]=Enum;
	}
	inline bool Count(int x,int y)
	{
		LL v=1ll*x*1000001+y;
		for(int x=v%Sz,i=H[x]; i; i=nxt[i])
			if(to[i]==v) return 1;
		return 0;
	}
}hs;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline LL Calc(int h,int l,int r)
{
	int t=std::min(h,l+r);
	if(!t) return 0;
	LL res=1ll*t*(t+3);
	if(t>l) res-=1ll*(t-l)*(t-l+1);
	if(t>r) res-=1ll*(t-r)*(t-r+1);
	return (res>>1)%mod;
}
int Calc1(int x,int y)
{
	int u=x,d=n-x,l=y,r=m-y;
	LL res=(Calc(u,l,r)+Calc(d,l,r)+Calc(l,u,d)+Calc(r,u,d))%mod;
	res=res-std::min(u,l)-std::min(u,r)-std::min(d,l)-std::min(d,r);
	return (res+mod)%mod;
}
void Calc2(int x1,int y1,int x2,int y2)
{
	if(!Legal(x1,y1)||!Legal(x2,y2)) return;
	int t=hs.Count(x1,y1)+hs.Count(x2,y2);
	++t2;
	if(t>=1) ++t3;//if更快啊。。
	if(t>=2) ++t3, ++t4;//就算是4个点，以i,j,k为顶点的正方形此时是算两个（i,j固定，k有两个）
//	++t2, t==1?(++t3):(t==2?(t3+=2,++t4):0);
}

int main()
{
	static int X[N],Y[N];
	n=read(),m=read(); int K=read();
	for(int i=1; i<=K; ++i) X[i]=read(),Y[i]=read(),hs.Insert(X[i],Y[i]);
	LL ans=0;
	for(int i=1,lim=std::min(n,m); i<=lim; ++i) ans+=1ll*(n-i+1)*(m-i+1)%mod*i%mod;
	for(int i=1; i<=K; ++i) ans-=Calc1(X[i],Y[i]);
	for(int i=1; i<=K; ++i)
	{
		int x1=X[i],y1=Y[i];
		for(int j=i+1; j<=K; ++j)
		{
			int x2=X[j], y2=Y[j], dx=x1-x2, dy=y1-y2;
			Calc2(x1+dy, y1-dx, x2+dy, y2-dx);//边
			Calc2(x1-dy, y1+dx, x2-dy, y2+dx);
			if((std::abs(dx)+std::abs(dy))&1) continue;
			int dx2=dx-dy>>1, dy2=dx+dy>>1;//对角线
			Calc2(x1-dx2, y1-dy2, x2+dx2, y2+dy2);
		}
	}
	ans=ans%mod+t2-t3/3+t4/6;
	printf("%lld\n",(ans%mod+mod)%mod);

	return 0;
}