雅克比迭代算法(Jacobi Iterative Methods) -- [ mpi , c++]

雅克比迭代，一般用来对线性方程组，进行求解。形如：
\(a_{11}*x_{1} + a_{12}*x_{2} + a_{13}*x_{3} = b_{1}\)　　
\(a_{21}*x_{1} + a_{22}*x_{2} + a_{23}*x_{3} = b_{2}\)　　
\(a_{31}*x_{1} + a_{32}*x_{2} + a_{33}*x_{3} = b_{3}\)　　
我们需要求解出\(x_{1}\)　，\(x_{２}\)　，\(x_{３}\)，我们对这组方程进行变换：
\(x_{1}=\frac{１}{a_{１1}}(b_{１} -a_{１2}*x_{２} -a_{１3}*x_{3})\)
　 \(x_{２}=\frac{１}{a_{21}}(b_{2} -a_{2１}*x_{１} -a_{23}*x_{3})\)
\(x_{３}=\frac{１}{a_{３1}}(b_{３} -a_{３１}*x_{１}-a_{３２}*x_{２})\)

我们不妨假设 \(x_{0}^{0}=(X_{1}^{0},X_{2}^{0},X_{3}^{0})\) ,当我们代入上述公式的时候，我们就会得到一组新的 \(x_{0}^{1}=(X_{1}^{1},X_{2}^{1},X_{3}^{1})\) ,此刻我们称之为一次迭代.
然后我们将得到的X1,X2,X3再次代入公式，我们将会得到第二次迭代, 当我们重复这种迭代的时候，我们会得到第K次迭代：
\(x^{k}=(X_{1}^{k},X_{2}^{k},X_{3}^{k})\) , \(k = 1,2,3...n\)
我们将其归纳成一般式子:

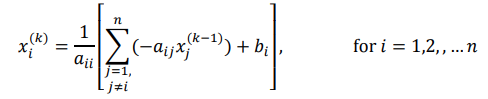
eg: 对于方程组：

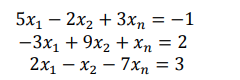
求解：
我们先将其变形：

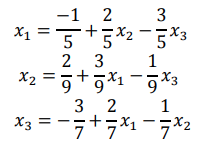
然后，我们假设：
并将其代入得到：

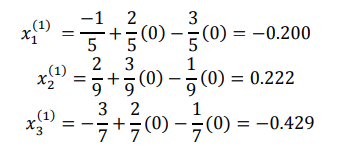
我们将得到的X1,x2,x3再次代入方程中，反复迭代,将会得到如下：

最终我们将会得到一个收敛值，该组值，就是我们得到的解（会非常的逼近真实解）

那么这种方法，也可以用来求解矩阵:
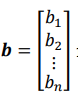对于方程： Ax =b ; 我们设定 A矩阵为： ,b矩阵为： ， x矩阵为：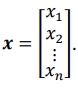
到这里，每个人都有自己的解法，直接的解法是将 x = \(A^{-1}\)b,但是A的逆矩阵\(A^{-1}\),计算较为复杂，我们这里需要一点小的tricks ,我们将A矩阵拆分成为一个对角矩阵D,下三角矩阵L,上三角矩阵U,即

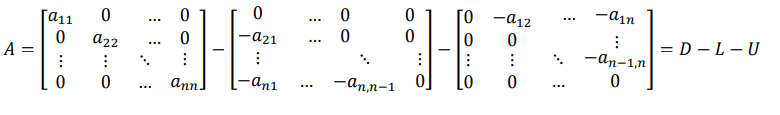
这样的话，公式 Ax = b 就变成了 ( D - L -U )x = b ,然后我们就可以得到：
Dx = b + (L+U)x ，当我们得到这个公式的时候，求解D的逆矩阵就容易了很多，我们得到D的逆矩阵为：

然后，我们将D移到右边变成:

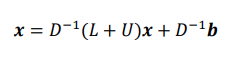
这个公式，和我们上面描述的雅克比迭代是不是长得很像，然后我们可以将其一般化为：

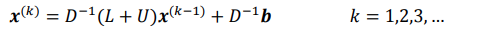
我们知道A是一个已知的常量矩阵，因而D,L,U都是已知矩阵，那么我们可以简化为：
\(T = D^{-1}*( L +U)\) , \(c = D^{-1}*b\) ;

根据这一个思想，我们可以得到一个伪代码：

实现代码为:

参考资料为:
https://www3.nd.edu/~zxu2/acms40390F12/Lec-7.3.pdf