【Foreign】魔法 [组合数][质因数分解]

魔法

Time Limit: 10 Sec  Memory Limit: 256 MB

Description

　　

Input

　　

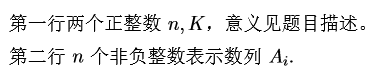
Output

　　仅一行一个整数表示答案。

Sample Input

　　4 10
　　7 2 8 5

Sample Output

　　2

HINT

　　

Solution

　　我们找一下规律，显然发现是就是Σa[i]*C(n-1,i-1)。然后问题主要就转化为了怎么快速求组合数C(n,i)在模一个非质数情况下的值。

　　首先我们先确定一个式子：

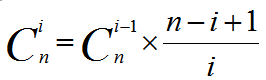
　　 然后我们立马想到了一个暴力分解质因数的方法。就是记录所有的(n-i+1)和(i)的质因数，然后用上面的质因数个数减去下面的质因数个数，剩下的乘起来，就不用求取模了。

　　但是我们发现，这样显然会TLE，我们考虑如何优化。优化的话显然就是要找到一个办法不把多的质因数都彻底分解出来。我们来继续思考：

　　我们可以先求出模数的质因数，再对于(n-i+1)和(i)分解质因数。这时候如果质因数和模数的质因数一样，由于不互质没有逆元，就把它记录下来，等下用快速幂乘起来就行了。那么这时候其余的质因数就可以直接求逆元了，由于模数不是质数，我们运用这个公式：（phi暴力求即可）

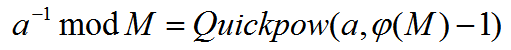
　　这样做的话，由于模数的质因数是个数有限的，拆解其余数可以减少很多部分，那么效率就可以得到保证啦。

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;

 const int Max = ;
 const int ONE = ;

 int n,x,MOD;
 int a[ONE];
 int f[Max],p[Max],p_num;
 int Num[Max];
 int Ans;

 int get()
 {
         int res=,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 int Quickpow(int a,int b)
 {
         int res=;
         while(b)
         {
             if(b&) res=(s64)res*a%MOD;
             a=(s64)a*a%MOD;
             b>>=;
         }
         return res;
 }

 void Deal_prime(int x)
 {
         for(int i=;i*i<=x;i++)
         if(!(x%i))
         {
             p[++p_num]=i;
             while(!(x%i)) x/=i;
         }
         if(x>) p[++p_num]=x;
 }

 int gcd(int a,int b) {int r=a%b; while(r) {a=b;b=r;r=a%b;} return b;}
 int phi(int x) {int res=; for(int i=;i<x;i++)if(gcd(i,x)==) res++;return res;}

 int Add(int x,int P)
 {
         if(!x || x==) return x;
         for(int i=;i<=p_num;i++)
         {
             while(!(x%p[i]))
             {
                 x/=p[i];
                 Num[p[i]]+=P;
             }
             if(x==) break;
         }
         return x;
 }

 int main()
 {
         n=get();    MOD=get();
         Deal_prime(MOD);
         int Phi = phi(MOD);

         int C=;
         int record=;
         for(int i=;i<=n;i++)
         {
             x=get();
             Ans = (Ans+ (s64)record * x % MOD) % MOD;
             if(i==n) break;
             C = (s64)C * Add(n-i,) % MOD * Quickpow(Add(i,-),Phi-) % MOD;
             record=C;
             for(int j=;j<=p_num;j++)
                 record= (s64)record * Quickpow(p[j],Num[p[j]]) % MOD;
         }

         printf("%d",Ans);
 }