@using (Html.BeginForm())

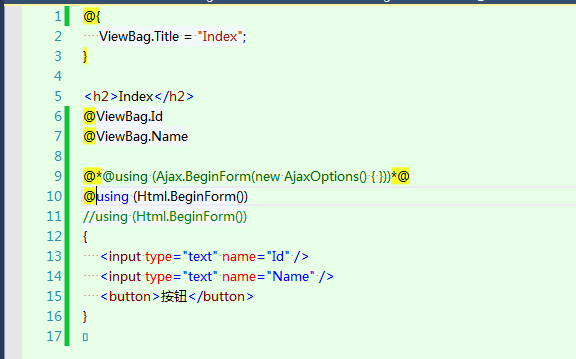
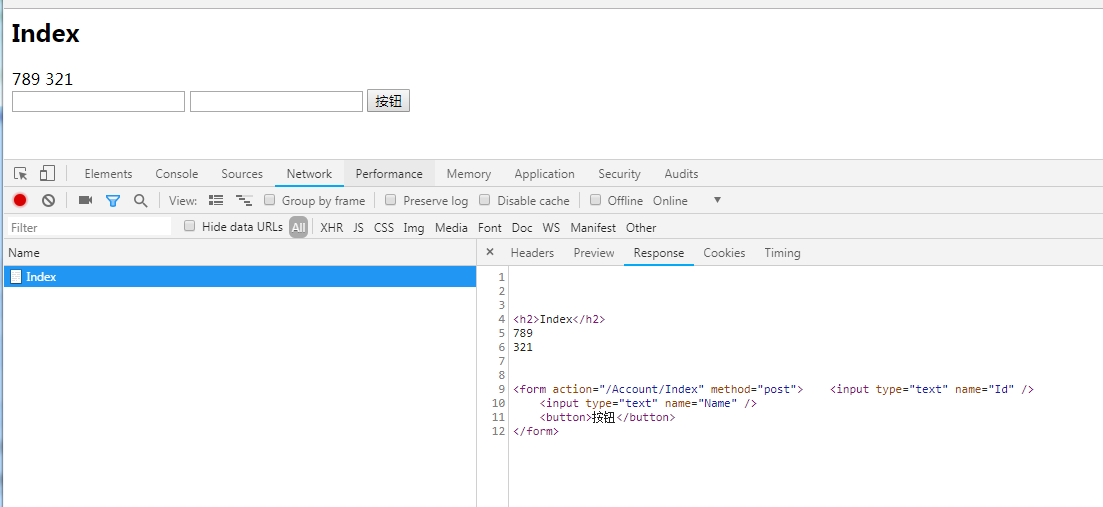
返回页面

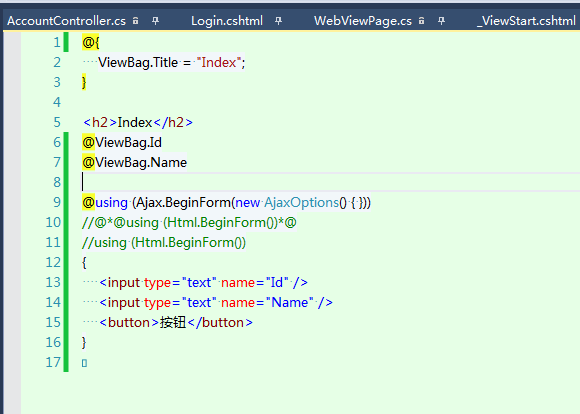
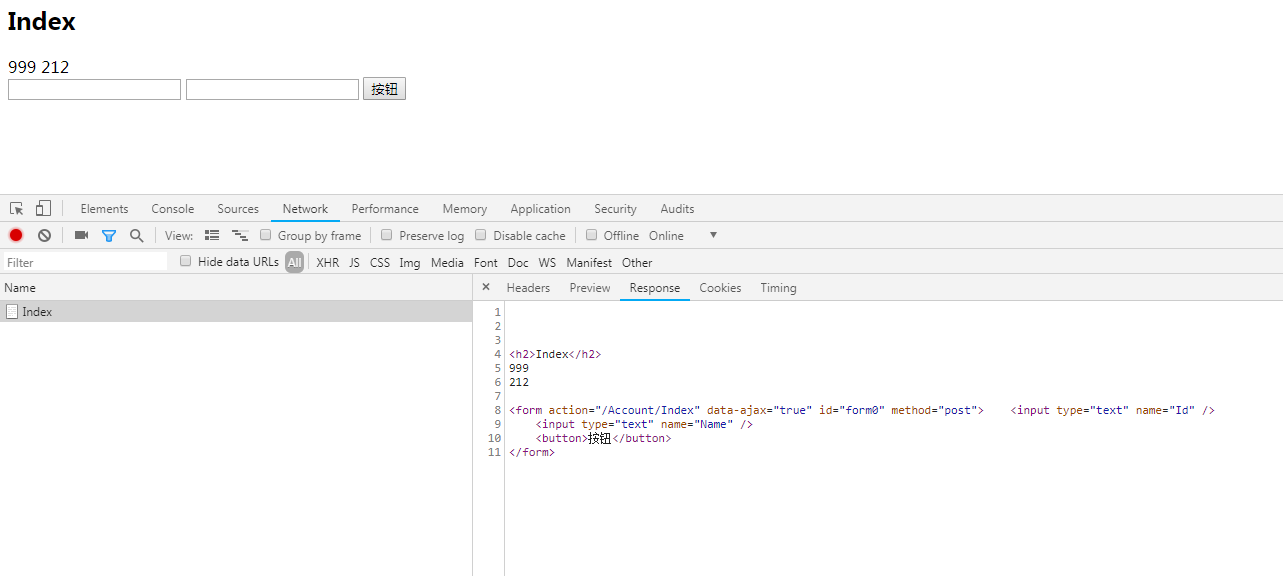
也是页面

都是返回页面 只是 多了一个 data-ajax="true"

@using (Html.BeginForm()) @using (Ajax.BeginForm(new AjaxOptions() { })) 区别的更多相关文章

  1. 爱上MVC3系列~Html.BeginForm与Ajax.BeginForm

    Html.BeginForm与Ajax.BeginForm都是MVC架构中的表单元素,它们从字面上可以看到区别,即Html.BeginForm是普通的表单提交,而Ajax.BeginForm是支持异步 ...

  2. Html.BeginForm())与Ajax.BeginForm()

     一.@using (Html.BeginForm())参数示例 1.指定表单提交方式和路径等 @using (Html.BeginForm("Index", "Home ...

  3. 转：MVC3系列：~Html.BeginForm与Ajax.BeginForm

    Html.BeginForm与Ajax.BeginForm都是MVC架构中的表单元素,它们从字面上可以看到区别,即Html.BeginForm是普通的表单提交,而Ajax.BeginForm是支持异步 ...

  4. MVC3系列~Html.BeginForm与Ajax.BeginForm

    Html.BeginForm与Ajax.BeginForm都是MVC架构中的表单元素,它们从字面上可以看到区别,即Html.BeginForm是普通的表单提交,而Ajax.BeginForm是支持异步 ...

  5. MVC小系列（十一）【Html.BeginForm与Ajax.BeginForm】

    Html.BeginForm与Ajax.BeginForm都是mvc的表单元素,前者是普通的表单提交,而后者是支持异步的表单提交,直接用mvc自带的Ajax.BeginForm就可以很容易完成一个异步 ...

  6. Html.BeginForm() vs Ajax.BeginForm() in MVC3

    我们知道,BeginForm()方法能创建一个Form标签,因此可以结合表单级的方法,在这个页面中.我一直在考虑Html.BeginForm()方法和Ajax.BeginForm()方法在MVC3中有 ...

  7. MVC Html.BeginForm 与 Ajax.BeginForm 使用总结

    最近采用一边工作一边学习的方式使用MVC5+EF6做一个Demo项目, 期间遇到不少问题, 一直处于研究状态, 没能来得及记录. 今天项目进度告一段落, 得以有空记录学习中遇到的一些问题. 由于MVC ...

  8. form表单和ajax表单提交（Html.BeginForm()、Ajax.BeginForm()）的差别

    有如下几种区别: 1. Ajax在提交.请求.接收时,都是异步进行的,网页不需要刷新: Form提交则是新建一个页面,哪怕是提交给自己本身的页面,也是需要刷新的: 2. A在提交时,是在后台新建一个请 ...

  9. 【转】利用Ajax.BeginForm提交文件

    Ajax.BeginForm @using (Ajax.BeginForm("YourAction", "YourController", new AjaxOp ...

随机推荐

  1. HDU 6351.Beautiful Now-暴力、全排列、思维 (2018 Multi-University Training Contest 5 1002)

    2018 Multi-University Training Contest 5 6351.Beautiful Now 题意就是交换任意两个数字,问你交换k次之后的最小值和最大值. 官方题解: 哇塞, ...

  2. Codeforces 626 C. Block Towers-二分 (8VC Venture Cup 2016-Elimination Round)

      C. Block Towers   time limit per test 2 seconds memory limit per test 256 megabytes input standard ...

  3. 主席树【bzoj3524(p3567)】[POI2014]Couriers

    Description 给一个长度为n的序列a.1≤a[i]≤n. m组询问,每次询问一个区间[l,r],是否存在一个数在[l,r]中出现的次数大于(r-l+1)/2.如果存在,输出这个数,否则输出0 ...

  4. 洛谷——P2556 [AHOI2002]黑白图像压缩

    P2556 [AHOI2002]黑白图像压缩 题目描述 选修基础生物基因学的时候, 小可可在家里做了一次图像学试验. 她知道:整个图像其实就是若干个图像点(称作像素)的序列,假定序列中像素的个数总是 ...

  5. 洛谷——P1655 小朋友的球

    P1655 小朋友的球 题目描述 @发源于 小朋友最近特别喜欢球.有一天他脑子抽了,从口袋里拿出了N个不同的球,想把它们放到M个相同的盒子里,并且要求每个盒子中至少要有一个球,他好奇有几种放法,于是尝 ...

  6. Floyd-弗洛伊德算法

    今天,研究一下谁都能看懂的弗洛伊德算法. 首先,弗洛伊德算法是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法. 这个算法需要一个用到一个二维数组啊a[][],而a[i][j]表示的就 ...

  7. centos7下自定义服务启动和自动执行脚本

    systemctl list-units --type=service #查看所有已启动的服务 systemctl enable httpd.service #加入开机自启动服务 systemctl ...

  8. [OpenJudge8782][划分DP]乘积最大

    乘积最大 总时间限制: 1000ms 内存限制: 65536kB [描述] 今年是国际数学联盟确定的“2000——世界数学年”,又恰逢我国著名数学家华罗庚先生诞辰90周年.在华罗庚先生的家乡江苏金坛, ...

  9. 如何让Adobe reader 记住上次pdf文档打开位置？

    菜单栏: Edit --> Preferences --> Documents --> 勾选 “Restore last view settings where reopening ...

  10. 如何用css做一个爱心

    摘要:HTML的标签都比较简单,入门非常的迅速,但是CSS是一个需要我们深度挖掘的东西,里面的很多样式属性掌握几个常用的便可以实现很好看的效果,下面我便教大家如何用CSS做一个爱心. 前期预备知识: ...