KM算法（运用篇）

传送门：KM算法---理解篇

最佳匹配

什么是完美匹配

如果一个二分图，X部和Y部的顶点数相等，若存在一个匹配包含X部与Y部的所有顶点，则称为完美匹配。
换句话说：若二分图X部的每一个顶点都与Y中的一个顶点匹配，**并且**Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完美匹配。

什么是完备匹配

如果一个二分图，X部中的每一个顶点都与Y部中的一个顶点匹配，**或者**Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完备匹配。

什么是最佳匹配

带权二分图的权值最大的完备匹配称为最佳匹配。

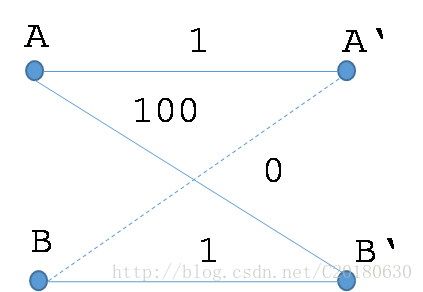
二分图的最佳匹配不一定是二分图的最大权匹配。

转化

可以添加一些权值为0的边，使得最佳匹配和最大权匹配统一起来。

KM算法

求二分图的最佳匹配有一个非常优秀的算法,可以做到O(N^3),这就是KM算法。该算法描述如下：

1.首先选择顶点数较少的为X部，初始时对X部的每一个顶点设置顶标，顶标的值为该点关联的最大边的权值，Y部的顶点顶标为0。

2.对于X部中的每个顶点，在相等子图中利用匈牙利算法找一条增广路径，如果没有找到，则修改顶标，扩大相等子图，继续找增广路径。当每个点都找到增广路径时，此时意味着每个点都在匹配中，即找到了二分图的完备匹配。该完备匹配即为二分图的最佳匹配。

什么是相等子图呢？因为每个顶点有一个顶标，如果我们选择边权等于两端点的顶标之和的边，它们组成的图称为相等子图。

如果从X部中的某个点Xi出发在相等子图中没有找到增广路径，我们是如何修改顶标的呢？如果我们没有找到增广路径，则我们一定找到了许多条从Xi出发并结束于X部的匹配边与未匹配边交替出现的路径，姑且称之为交错树。我们将交错树中X部的顶点顶标减去一个值d，交错树中属于Y部的顶点顶标加上一个值d。这个值后面要讲它如何计算。那么我们会发现：

两端都在交错树中的边(i,j)，其顶标和没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。
两端都不在交错树中的边(i,j)，其顶标也没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。
X端不在交错树中，Y端在交错树中的边(i,j)，它的顶标和会增大。它原来不属于相等子图，现在仍不属于相等子图。
X端在交错树中，Y端不在交错树中的边(i,j),它的顶标和会减小。也就说，它原来不属于相等子图，现在可能进入了相等子图，因而使相等子图得到了扩大。
我们修改顶标的目的就是要扩大相等子图。为了保证至少有一条边进入相等子图，我们可以在交错树的边中寻找顶标和与边权之差最小的边,这就是前面说的d值。将交错树中属于X部的顶点减去d，交错树中属于Y部的顶点加上d。则可以保证至少有一条边扩充进入相等子图。

3.当X部的所有顶点都找到了增广路径后，则找到了完备匹配，此完备匹配即为最佳匹配。

相等子图的若干性质

在任意时刻，相等子图上的最大权匹配一定小于等于相等子图的顶标和。
在任意时刻，相等子图的顶标和即为所有顶点的顶标和。
扩充相等子图后，相等子图的顶标和将会减小。
当相等子图的最大匹配为原图的完备匹配时，匹配边的权值和等于所有顶点的顶标和，此匹配即为最佳匹配

以上就是KM算法的基本思路。但是朴素的实现方法，时间复杂度为O(n4)——需要找O(n)次增广路，每次增广最多需要修改O(n)次顶标，每次修改顶标时由于要枚举边来求d值，复杂度为O(n2)。实际上KM算法的复杂度是可以做到O(n3)的。我们给每个Y顶点一个“松弛量”函数slack，每次开始找增广路时初始化为无穷大。在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack[j]变成原值与 A[i]+B[j]-w[i,j]的较小值。这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点：修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去d

模板一，用全局变量minz表示边权和顶标最小的差值，省去slack数组

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<map>
 using namespace std;
 typedef long long ll;
 const int maxn =  + ;
 const int INF = 0x3f3f3f3f;
 
 int wx[maxn], wy[maxn];//每个点的顶标值（需要根据二分图处理出来）
 int cx[maxn], cy[maxn];//每个点所匹配的点
 int visx[maxn], visy[maxn];//每个点是否加入增广路
 int cntx, cnty;//分别是X和Y的点数
 int Map[maxn][maxn];//二分图边的权值
 int minz;//边权和顶标最小的差值
 
 bool dfs(int u)//进入DFS的都是X部的点
 {
     visx[u] = ;//标记进入增广路
     for(int v = ; v <= cnty; v++)
     {
         if(!visy[v] && Map[u][v] != INF)//如果Y部的点还没进入增广路,并且存在路径
         {
             int t = wx[u] + wy[v] - Map[u][v];
             if(t == )//t为0说明是相等子图
             {
                 visy[v] = ;//加入增广路
 
                 //如果Y部的点还未进行匹配
                 //或者已经进行了匹配，可以从原来的匹配反向找到增广路
                 //那就可以进行匹配
                 if(cy[v] == - || dfs(cy[v]))
                 {
                     cx[u] = v;
                     cy[v] = u;//进行匹配
                     return ;
                 }
             }
             else if(t > )//此处t一定是大于0，因为顶标之和一定>=边权
             {
                 minz = min(minz, t);//边权和顶标最小的差值
             }
         }
     }
     return false;
 }
 
 int KM()
 {
     memset(cx, -, sizeof(cx));
     memset(cy, -, sizeof(cy));
     memset(wx, , sizeof(wx));//wx的顶标为该点连接的边的最大权值
     memset(wy, , sizeof(wy));//wy的顶标为0
     for(int i = ; i <= cntx; i++)//预处理出顶标值
     {
         for(int j = ; j <= cnty; j++)
         {
             if(Map[i][j] == INF)continue;
             wx[i] = max(wx[i], Map[i][j]);
         }
     }
     for(int i = ; i <= cntx; i++)//枚举X部的点
     {
         while()
         {
             minz = INF;
             memset(visx, , sizeof(visx));
             memset(visy, , sizeof(visy));
             if(dfs(i))break;//已经匹配正确
 
             //还未匹配，将X部的顶标减去minz，Y部的顶标加上minz
             for(int j = ; j <= cntx; j++)
                 if(visx[j])wx[j] -= minz;
             for(int j = ; j <= cnty; j++)
                 if(visy[j])wy[j] += minz;
         }
     }
 
     int ans = ;//二分图最优匹配权值
     for(int i = ; i <= cntx; i++)
         if(cx[i] != -)ans += Map[i][cx[i]];
     return ans;
 }
 int n, k;
 int main()
 {
     while(scanf("%d", &n) != EOF)
     {
         for(int i = ; i <= n; i++)
         {
             for(int j = ; j <= n; j++)
                 scanf("%d", &Map[i][j]);
         }
         cntx = cnty = n;
         printf("%d\n", KM());
     }
     return ;
 }

模板二，用slack数组（对于完全图的优化很快）

和全局变量不同的是，全局变量在每次while循环中都需要赋值成INF，每次求出的是所有点的最小值，而slack数组在每个while外面就初始化好，每次while循环slack数组的每个值都在用到，一次增广路中求出的slack值会更准确，循环次数比全局变量更少

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<map>
 using namespace std;
 typedef long long ll;
 const int maxn =  + ;
 const int INF = 0x3f3f3f3f;
 
 int wx[maxn], wy[maxn];//每个点的顶标值（需要根据二分图处理出来）
 int cx[maxn], cy[maxn];//每个点所匹配的点
 int visx[maxn], visy[maxn];//每个点是否加入增广路
 int cntx, cnty;//分别是X和Y的点数
 int Map[maxn][maxn];//二分图边的权值
 int slack[maxn];//边权和顶标最小的差值
 
 bool dfs(int u)//进入DFS的都是X部的点
 {
     visx[u] = ;//标记进入增广路
     for(int v = ; v <= cnty; v++)
     {
         if(!visy[v] && Map[u][v] != INF)//如果Y部的点还没进入增广路,并且存在路径
         {
             int t = wx[u] + wy[v] - Map[u][v];
             if(t == )//t为0说明是相等子图
             {
                 visy[v] = ;//加入增广路
 
                 //如果Y部的点还未进行匹配
                 //或者已经进行了匹配，可以从原来的匹配反向找到增广路
                 //那就可以进行匹配
                 if(cy[v] == - || dfs(cy[v]))
                 {
                     cx[u] = v;
                     cy[v] = u;//进行匹配
                     return ;
                 }
             }
             else if(t > )//此处t一定是大于0，因为顶标之和一定>=边权
             {
                 slack[v] = min(slack[v], t);
                 //slack[v]存的是Y部的点需要变成相等子图顶标值最小增加多少
             }
         }
     }
     return false;
 }
 
 int KM()
 {
     memset(cx, -, sizeof(cx));
     memset(cy, -, sizeof(cy));
     memset(wx, , sizeof(wx));//wx的顶标为该点连接的边的最大权值
     memset(wy, , sizeof(wy));//wy的顶标为0
     for(int i = ; i <= cntx; i++)//预处理出顶标值
     {
         for(int j = ; j <= cnty; j++)
         {
             if(Map[i][j] == INF)continue;
             wx[i] = max(wx[i], Map[i][j]);
         }
     }
     for(int i = ; i <= cntx; i++)//枚举X部的点
     {
         memset(slack, INF, sizeof(slack));
         while()
         {
 
             memset(visx, , sizeof(visx));
             memset(visy, , sizeof(visy));
             if(dfs(i))break;//已经匹配正确
 
             int minz = INF;
             for(int j = ; j <= cnty; j++)
                 if(!visy[j] && minz > slack[j])
                     //找出还没经过的点中，需要变成相等子图的最小额外增加的顶标值
                     minz = slack[j];
             //和全局变量不同的是，全局变量在每次while循环中都需要赋值成INF，每次求出的是所有点的最小值
             //而slack数组在每个while外面就初始化好，每次while循环slack数组的每个值都在用到
             //在一次增广路中求出的slack值会更准确，循环次数比全局变量更少
 
             //还未匹配，将X部的顶标减去minz，Y部的顶标加上minz
             for(int j = ; j <= cntx; j++)
                 if(visx[j])wx[j] -= minz;
             for(int j = ; j <= cnty; j++)
                 //修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去minz
                 if(visy[j])wy[j] += minz;
                 else slack[j] -= minz;
         }
     }
 
     int ans = ;//二分图最优匹配权值
     for(int i = ; i <= cntx; i++)
         if(cx[i] != -)ans += Map[i][cx[i]];
     return ans;
 }
 int n, k;
 int main()
 {
     while(scanf("%d", &n) != EOF)
     {
         for(int i = ; i <= n; i++)
         {
             for(int j = ; j <= n; j++)
                 scanf("%d", &Map[i][j]);
         }
         cntx = cnty = n;
         printf("%d\n", KM());
     }
     return ;
 }