【BZOJ 2693】jzptab（莫比乌斯+分块）

2693: jzptab

Description

Input

一个正整数T表示数据组数

接下来T行 每行两个正整数 表示N、M

Output

T行 每行一个整数 表示第i组数据的结果

Sample Input

1

4 5

Sample Output

122

HINT
T <= 10000

N, M<=10000000

 

 

【分析】

　　bzoj2154的进化版！多组。。

　　根据bzoj2154的推导我们有：

　　

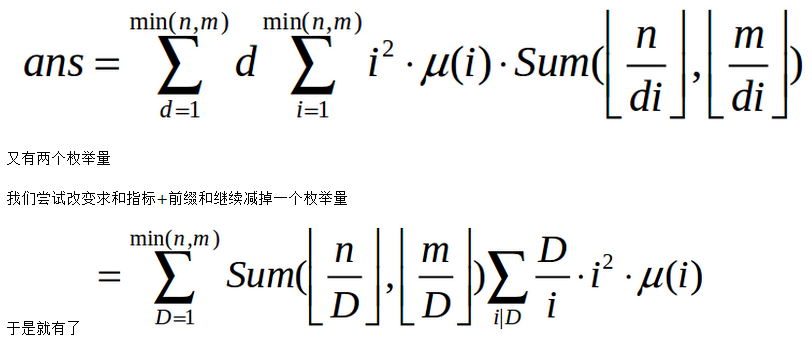
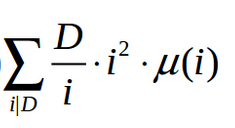　对于这个把它放入线性筛里面预处理就好了。

 

 

　　首先证明f[n]=∑i*mu[i](i|n)为积性函数：

　　设函数g[n]=n*mu[n],那么f=1*g，1和g都是积性函数，所以f也是积性函数。

 

　　线性筛的时候，当i%prime[j]!=0 由积性函数得，f[i*prime[j]]=f[i]*f[prime[j]]

　　当i%prime[j]==0时，若再加入prime[j],mu值为0，所以对答案没有影响。即f[i*prime[j]]=f[i]。

　　想这里的时候还是有思维局限，要记住当有一个质因子质数大于1时，mu值就为0了，这个特点前面一题也用到过！！

 

　　还有一个不是很懂的地方就是为什么每次加进去时都要MOD成正数，表示不知道化简之后为什么不能加一个负数进去~~导致WA很久~~

 

代码如下：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cmath>
 using namespace std;
 #define Mod 100000009
 #define Maxn 10000010
 #define LL long long

 LL mu[Maxn],pri[Maxn],g[Maxn],h[Maxn],pl;
 bool q[Maxn];

 LL mymin(LL x,LL y) {return x<y?x:y;}

 void get_mu(LL mx)
 {
     pl=;
     memset(q,,sizeof(q));
     mu[]=;g[]=;
     for(LL i=;i<=mx;i++)
     {
         if(q[i])
         {
             pri[++pl]=i;
             mu[i]=-;
             g[i]=+i*mu[i];
         }
         for(LL j=;j<=pl;j++)
         {
             if(i*pri[j]>mx) break;
             q[i*pri[j]]=;
             if(i%pri[j]==) mu[i*pri[j]]=,g[i*pri[j]]=g[i];
             else mu[i*pri[j]]=-mu[i],g[i*pri[j]]=(g[i]*g[pri[j]])%Mod;
             if(i%pri[j]==) break;
         }
     }
     for(LL i=;i<=mx;i++) g[i]=(i*g[i])%Mod;
     h[]=g[];
     for(LL i=;i<=mx;i++) h[i]=(h[i-]+g[i])%Mod;
 }

 LL get_sum(LL x,LL y)
 {
     return ( ( ((x+)*x/)%Mod )*( ((y+)*y/)%Mod ) )%Mod;
 }

 LL get_ans(LL n,LL m)
 {
     LL ans=;

     LL sq=(LL)ceil(sqrt((double)m));
     for(LL i=;i<=mymin(sq,n);i++)
     {
         ans=(ans+(g[i]%Mod+Mod)%Mod*get_sum(n/i,m/i) )%Mod;
     }

     for(LL i=sq+;i<=n;)
     {
         LL x=n/i,y=m/i;
         LL r1=n/x+,r2=m/y+;
         LL r=mymin(r1,r2);
         if(r>m+) r=m+;
         // if((((h[r-1]-h[i-1])%Mod+Mod)%Mod)<0) while(1);
         ans=( ans+(((h[r-]-h[i-])%Mod+Mod)%Mod)*get_sum(x,y) )%Mod;
         i=r;
     }
     return ans;
 }

 int main()
 {
     int T;
     T=;
     scanf("%d",&T);
     get_mu();

     while(T--)
     {
         LL n,m,t;
         scanf("%lld%lld",&n,&m);
         if(n>m) t=n,n=m,m=t;

         LL ans=get_ans(n,m);

         printf("%lld\n",ans);
     }
     return ;
 }

[BZOJ 2693]

 

 

2016-08-30 16:49:26