P1140 相似基因（字符串距离，递推）

题目链接：

https://www.luogu.org/problemnew/show/P1140

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了44种核苷酸，简记作A,C,G,TA,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATGAGTGATG和GTTAGGTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

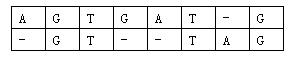
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

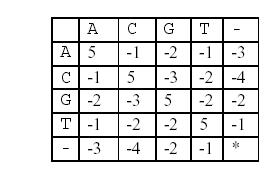
那么相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因为两个基因的对应方法不唯一，例如又有：

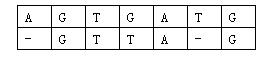
相似度为：(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,TA,C,G,T四个字母。1 \le1≤序列的长度\le 100≤100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1： 复制

7 AGTGATG
5 GTTAG

输出样例#1： 复制

14

解题思路：

动态规划。难点在于理解递推关系。

以输入

3 ATG
2 CG

为例：

设f(i,j)为第一个字符串的前i个字符与第二个字符串的前j个字符之间的距离，那么当计算f(3,2)时的可能情况有：

情况1：
ATG
-CG
此时f(3,2)=f(2,1)+dis('G','G')

情况2：
ATG-
--CG
此时b[1]与空格相对，f(3,2)=f(3,1)+dis('-','G')

情况3：
ATG
CG-
此时a[2]与空格相对，f(3,2)=f(2,2)+dis('G','-')

综上，递推公式为：

$ f(i,j)=max\{f(i-1,j-1)+dis(i,j),f(i-1,j)+dis(i,4),f(i,j-1)+dis(4,j)\} $

#include<iostream>
#include<cstdio>
#include<string>
#include<map>
using namespace std;
int mp[5][5]={5,-1,-2,-1,-3,
              -1,5,-3,-2,-4,
              -2,-3,5,-2,-2,
              -1,-2,-2,5,-1,
              -3,-4,-2,-1,0};
int f[110][110];
string a,b;
map<char,int> mpp;
int main(){
    int l1,l2;
    cin>>l1>>a>>l2>>b;
    mpp['A']=0;mpp['C']=1;mpp['G']=2;mpp['T']=3;mpp['-']=4;
    for(int i=0;i<=l1;i++) for(int j=0;j<=l2;j++) f[i][j]=-999999999;//初始化成很小的值，因为字符与字符之间的距离可能为负数

    f[0][0]=0;

    for(int i=1;i<=l1;i++) f[i][0]=f[i-1][0]+mp[mpp[a[i-1]]][4];//边界处理，需要累积之前的记录
    for(int j=1;j<=l2;j++) f[0][j]=f[0][j-1]+mp[4][mpp[b[j-1]]];//

    for(int i=1;i<=l1;i++){
        int na=mpp[a[i-1]];
        for(int j=1;j<=l2;j++){
            int nb=mpp[b[j-1]];
            f[i][j]=max(f[i][j],f[i-1][j-1]+mp[na][nb]);//a[i]与b[j]匹配
            f[i][j]=max(f[i][j],f[i-1][j]+mp[na][4]);//a[i]与空格匹配
            f[i][j]=max(f[i][j],f[i][j-1]+mp[4][nb]);//空格与b[j]匹配
        }
    }

    printf("%d\n",f[l1][l2]);
}