并查集算法Union-Find的思想、实现以及应用

并查集算法，也叫Union-Find算法，主要用于解决图论中的动态连通性问题。

Union-Find算法类

这里直接给出并查集算法类UnionFind.class，如下：

/**
 * Union-Find 并查集算法
 * @author Chiaki
 */
public class UnionFind {
    // 连通分量个数
    private int count;
    // 存储若干棵树
    private int[] parent;
    // 记录树的"重量"
    private int[] size;
    // 构造函数
    public UnionFind(int count) {
        this.count = count;
        parent = new int[count];
        size = new int[count];
        for (int i = 0; i < count; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    // 连通函数
    public void union(int p, int q) {
        // 如果节点p和q已经连接，直接返回
        if (connected(p,q)) return;
        // 找到节点p和节点q的根节点
        int rootP = find(p);
        int rootQ = find(q);
        if (size[rootP] > size[rootQ]) {
            parent[rootQ] = rootP;
            size[rootP] += size[rootQ];
        } else {
            parent[rootP] = rootQ;
            size[rootQ] += size[rootP];
        }
        count--;
    }
    // 判断是否连通
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }
    // 寻找根节点
    public int find(int x) {
        while (parent[x] != x) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    // 返回连通分量个数
    public int count() {
        return count;
    }
}

下面逐步解释Union-Find算法类中的变量定义以及相关函数。

成员变量

可以看到该类中定义了三个成员变量，分别是int count、int[] parent以及int[] size。

int count：可以理解为连通分量的个数。

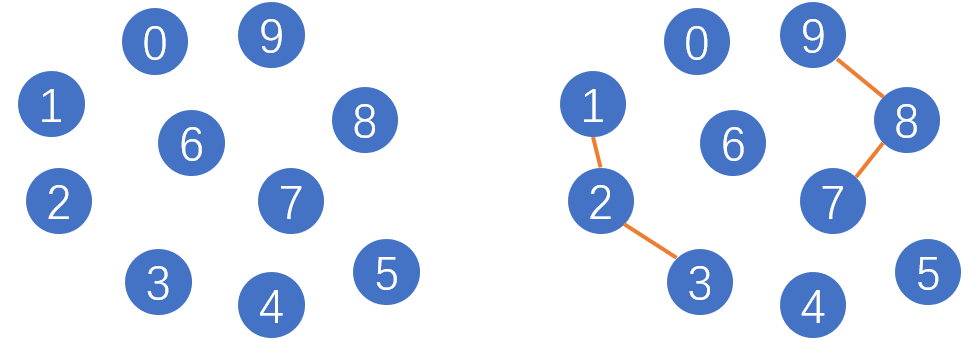
如上左图所示，共有10个节点（分量），此时连通分量的个数为10。如上右图所示，在进行连通操作（union）后，分量之间存在了连接关系（connected），因此此时的连通分量个数为6。

int[] parent：定义父节点数组。说到父节点数组，这里使用多棵树来表示连通性。规定树中的每个节点都有一个指针指向其父节点。一开始没有连通，此时每个节点指向父节点的指针都是指向自己，也就是根节点；当两个节点被连通，就让其中的任意一个节点的根节点接到另一个节点的根节点上，如下图所示。

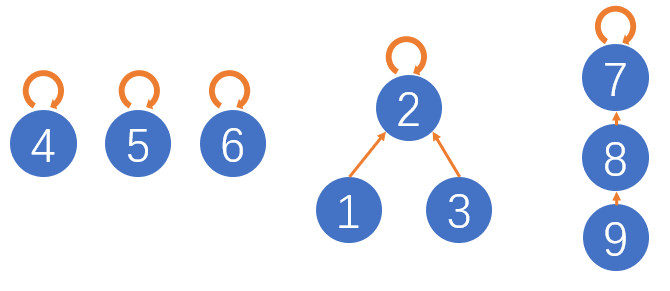
此时，可以得到：若节点p和节点q连通，那么它们一定有相同的根节点。

int[] size：记录每一棵树中节点的数量，称之为树的重量，以此方便对树的平衡性进行优化。如上张图所示，如果要把节点3和节点7连接（union），此时树的情况如下图所示：

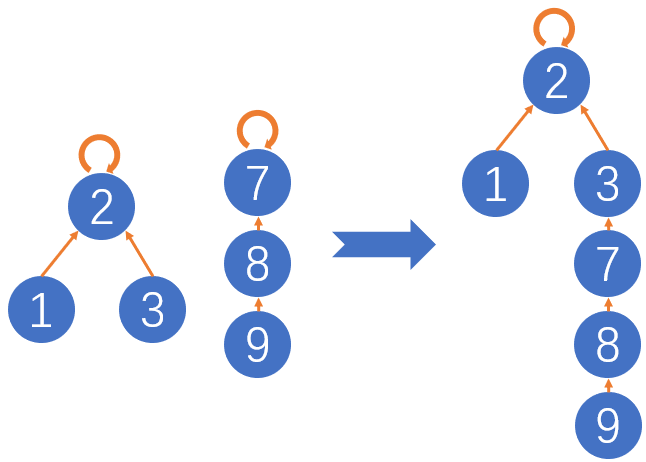
此时，可以看出，树的平衡性出现了问题，因此我们需要借助树的重量，即int[] size数组对节点的连接操作（union）进行平衡性优化。

构造函数

UnionFind类构造函数的参数为int n，即初始的节点数目，亦即初始连通分量的个数。在进行初始化操作时，主要是初始化父节点数组int[] parent以及每棵树中节点的数目数组int[] size。在初始情况下，每个节点的父节点都是自身，而每棵树中节点的个数都是1，因此构造函数如下：

public UnionFind(int count) {
    this.count = count;
    parent = new int[count];
    size = new int[count];
    for (int i = 0; i < count; i++) {
        parent[i] = i;
        size[i] = 1;
    }
}

其他函数

在上面的介绍中，我们知道，在UnionFind类中最重要的操作就是连接（union）操作。然而，在将节点p和节点q连接时，需要把一个节点（假定为节点p）的指针指向另一个节点（假定为节点q）的父节点，因此，我们需要先实现一个int find(int x)函数来找到一个节点的父节点，如下所示：

public int find(int x) {
    while (parent[x] != x) {
        parent[x] = parent[parent[x]];
        x = parent[x];
    }
    return x;
}

另外，实现boolean connected(int p, int q)函数判断节点p和节点q是否处于连接状态，如下：

public boolean connected(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    return rootP == rootQ;
}

在实现int find(int x)函数和boolean connected(int p, int q)函数后，接下来要实现最关键的连接操作，即void union(int p, int q)函数，如下所示：

public void union(int p, int q) {
    // 如果节点p和q已经连接，直接返回
    if (connected(p,q)) return;
    // 找到节点p和节点q的根节点
    int rootP = find(p);
    int rootQ = find(q);
    // 根据size数组进行平衡化操作：小树接到大树下
    if (size[rootP] > size[rootQ]) {
        parent[rootQ] = rootP;
        size[rootP] += size[rootQ];
    } else {
        parent[rootP] = rootQ;
        size[rootQ] += size[rootP];
    }
    // 连接完成后，连通分量减一
    count--;
}

最后，完成连通分量计数函数int count()，如下：

public int count() {
    return count;
}

Union-Find算法应用

在介绍完并查集算法类UnionFind.class后，下面来看看该算法的应用。

朋友圈/好友关系问题

这个问题是并查集的一个典型应用，印象中猿辅导的算法手撕中这个题出现的频率比较高。问题描述如下：

LeetCode547

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果 M[i][j]= 1 ，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。输入输出示例如下：

输入：

[[1,1,0],

[1,1,0],

[0,0,1]]

输出：2

利用并查集来解决该问题（假设UnionFind.class已定义，下同），如下：

class Solution {
    public int findCircleNum(int[][] M) {
        int n = M.length;
        UnionFind uf = new UnionFind(n);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (M[i][j] == 1) uf.union(i, j);
            }
        }
        return uf.count();
    }
}

岛屿数量

岛屿数量问题其实也是互联网大厂常问的题目之一，除了采用DFS来实现，并查集也可以用于解决这类问题。问题描述如下：

LeetCode200

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外，你可以假设该网格的四条边均被水包围。输入输出示例如下：

输入：grid = [

["1","1","1","1","0"],

["1","1","0","1","0"],

["1","1","0","0","0"],

["0","0","0","0","0"]

]

输出：1

采用并查集方法解决：

class Solution {
    public int numIslands(char[][] grid) {
        int r = grid.length;
        if (r == 0) return 0;
        int c = grid[0].length;
        int size = r * c;
        // 方向数组（向下和向右的坐标偏移）
        int[][] directions = {{1, 0}, {0, 1}};
        // +1表示虚拟水域，认为网格四条边被水包围
        UnionFind uf = new UnionFind(size + 1);
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                if (grid[i][j] == '1') {
                    for (int[] direction : directions) {
                        int newX = i + direction[0];
                        int newY = j + direction[1];
                        if (newX < r && newY < c && grid[newX][newY] == '1') {
                            uf.union(c * i + j, c * newX + newY);
                        }
                    }
                } else {
                        // 如果不是陆地，则所有水域与虚拟水域连接
                        uf.union(c * i + j, size);
                }
            }
        }
        // 减去虚拟水域
        return uf.count() - 1;
    }
}

等式方程的可满足性

题目描述如下：

LeetCode990

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同形式之一：a==b 或 a!=b。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。 输入输出示例如下：

输入：[ab, bc, a==c]

输出：true

输入：[ab, b!=c, ca]

输出：false

采用并查集算法解决该问题，如下：

class Solution {
    public boolean equationsPossible(String[] equations) {
        // 可能出现的26个字母
        UnionFind uf = new UnionFind(26);
        // 将相等的字母进行连接
        for (String e : equations) {
            if (e.charAt(1) == '=') {
                char x = e.charAt(0);
                char y = e.charAt(3);
                uf.union(x - 'a', y - 'a');
            }
        }
        // 若已经成立的相等关系被打破就返回false
        for (String e : equations) {
            if (e.charAt(1) == '!') {
                char x = e.charAt(0);
                char y = e.charAt(3);
                if (uf.connected(x - 'a', y - 'a')) return false;
            }
        }
        return true;
    }
}

Union-Find算法的简单总结

并查集算法主要是解决图中的动态连通性问题。对于类似岛屿数量的问题，注意在初始化并查集时做到+1来表示一个虚拟节点，同时对于其中的二维数组可以采用方向数组int[] directions = {{1, 0}, {0, 1}}来规范和简化代码。对于等式方程的可满足性，主要是利用了并查集算法的等价特点。

参考

labuladong在leetcode547的题解