题解：POI2012 Salaries

题解：POI2012 Salaries

Description

The Byteotian Software Corporation (BSC) has \(n\) employees.

In BSC's strict hierarchy, each employee has a direct supervisor, except the CEO, to whom all other BSC employees answer, directly or not.

Each employee has a unique monthly salary, and all their salaries range from 1 to \(n\) bythalers.

Each supervisor earns more than each of their subordinates.

According to Byteotian law, the salaries of employees on certain posts may be publicly disclosed.

Furthermore, if the salary of an employee is disclosed, then the salary of their supervisor is also disclosed.

The Byteotian Internal Revenue Anti-Corruption Service (BIRAS) has decided to investigate BSC.

Before BIRAS enters BSC with a warrant, they intend to learn the salaries of all BSC employees that are not disclosed but can be determined from those that are disclosed.

题意：

给一棵 \(n\) 个结点的树，点权取 \(1 \sim n\) 且 各不相同。

满足任意非根结点的权值一定比它的父节点权值小。

现在自顶向下地已知一些点的权值（即若某非根点权值已知，其父节点的权值也一定已知），

问哪些点的权值能唯一确定。

\(n \leq 1e6\)

Algorithm

这是一道 十分有趣 而 一言难尽 的题目。

我们先从两个例子入手，试图理解一下「唯一确定」的意思。

例一

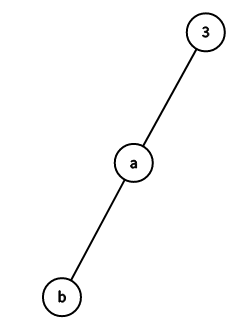
在这里，由于点 \(b\) 是点 \(3\) 的孙子结点，最大只能取 \(1\) ，因此唯一确定 \(b = 1\)

同时，点 \(a\) 是点 \(3\) 的儿子结点，可能的取值有 \(1, 2\) ，但因为 \(b = 1\) ，所以唯一确定 \(a = 2\)

例二

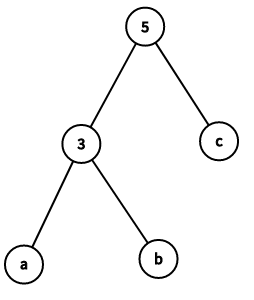
此处 \(a, b\) 都是 \(3\) 的子节点，他们的取值可能为 \(1, 2\) ，但并不能唯一确定一种对应关系。

\(c\) 是 \(5\) 的子节点，可能的取值有 \(1, 2, 4\) 。但因为 \(a, b\) 对应 \(1, 2\) ，只能有 \(c = 4\) ，这也是唯一确定的。

揆诸上例与题面自顶向下给权的性质，我们容易发现：

1. 对于任意一个未确定的结点，它的可能取值范围总是 \((0,x_i]\) ，

   其中， \(x_i\) 是由树的结构与已知点权共同决定的。

2. 一个点的权能被唯一确定，当且仅当其取值范围为 \((x_i - 1, x_i]\)

3. 当我们确定了 \(k\) 个结点的取值后，剩余的未确定结点的取值范围就会变化为 \((k, x_i]\)

4. 确定点权的顺序总是从小到大的。

（写成左开右闭的形式仅仅是为了规避区间左右端点相等的写法，没别的意思）

接下来只要模拟上述的推理即可。

我们可以首先一次 DFS 遍历整棵树，根据树结构维护每个点可能的最大取值。

特别注意此处有个坑，如果仅根据点的祖先结点取值和深度计算 \(x_i\) 的话代码就是错误的。

经过这种方法计算出的值 \(x'_i\) 可能已经被某个已知点取了，你需要尝试不断减少 \(x'_i\) 的值直到其符合定义为止。

这个"不断减少"的过程可以预处理出来。

DFS 之后，我们可以根据最大取值将点排序，再依次考虑每个权是否可以被确定或唯一确定。

这个算法描述起来还挺模糊的……不如直接读代码：

#include<bits/stdc++.h>
using namespace std;

template<class T>
inline void read(T &x)
{
	char c = getchar();	x = 0;
	while(c < '0' || '9' < c)	c = getchar();
	while('0' <= c && c <= '9')
	{
		x = (x << 1) + (x << 3) + c - 48;
		c = getchar();
	}
}

const int INF = 0x7f7f7f7f;
typedef pair<int, int> Node;
vector<Node> ord;

template<const int N, const int M>
class Tree {
private:
	int beg[N], nex[M], tar[M], len;
public:
	int vap[N], van[N];
	bool vis[N];

	Tree():len(1) {}
	inline void add_egde(int a, int b)
	{
		++len, tar[len] = b;
		nex[len] = beg[a], beg[a] = len;
	}

	void dfs(int cur, int val)
	{
		if(!vap[cur])	ord.push_back(Node(val, cur));
		for(int i = beg[cur]; i; i = nex[i])
		{
			if(vap[tar[i]])	dfs(tar[i], vap[tar[i]]);
			else			dfs(tar[i], van[val - 1]);
		}
	}
};

Tree<1048576, 1048576> T;
int main()
{
	int n, rot;

	read(n);
	for(int i = 1, x; i <= n; ++i)
	{
		read(x), read(T.vap[i]);

		if(x == i)	rot = i, T.vap[i] = n;
		else		T.add_egde(x, i);

		if(T.vap[i])
			T.vis[T.vap[i]] = true;
	}

	for(int i = 1; i <= n; ++i)
	{
		if(T.vis[i])	T.van[i] = T.van[i - 1];
		else			T.van[i] = i;
	}

	T.dfs(rot, n);
	sort(ord.begin(), ord.end());

	int done = 0, len = ord.size();
	for(int i = 1, j = 0; i <= n; i++)
	{
		if(T.vis[i])	done++;
		else
		{
			int cnt = 0;
			while(j < len && ord[j].first == i)	j++, cnt++;
			if(cnt == 1 && done == i - 1)
				T.vap[ord[j - 1].second] = i;
			done += cnt;
		}
	}

	for(int i = 1; i <= n; ++i)
		printf("%d\n", T.vap[i]);

	return 0;
}