（在模仿中精进数据可视化03）OD数据的特殊可视化方式

本文完整代码已上传至我的Github仓库https://github.com/CNFeffery/FefferyViz

1 简介

　　OD数据是交通、城市规划以及GIS等领域常见的一类数据，特点是每一条数据都记录了一次OD（O即Origin，D即Destination）行为的起点与终点坐标信息。

　　而针对OD数据常见的可视化表达方式为弧线图，譬如图1所示的例子，就针对纽约曼哈顿等区域的某时间段Uber打车记录上下车点数据进行展示：

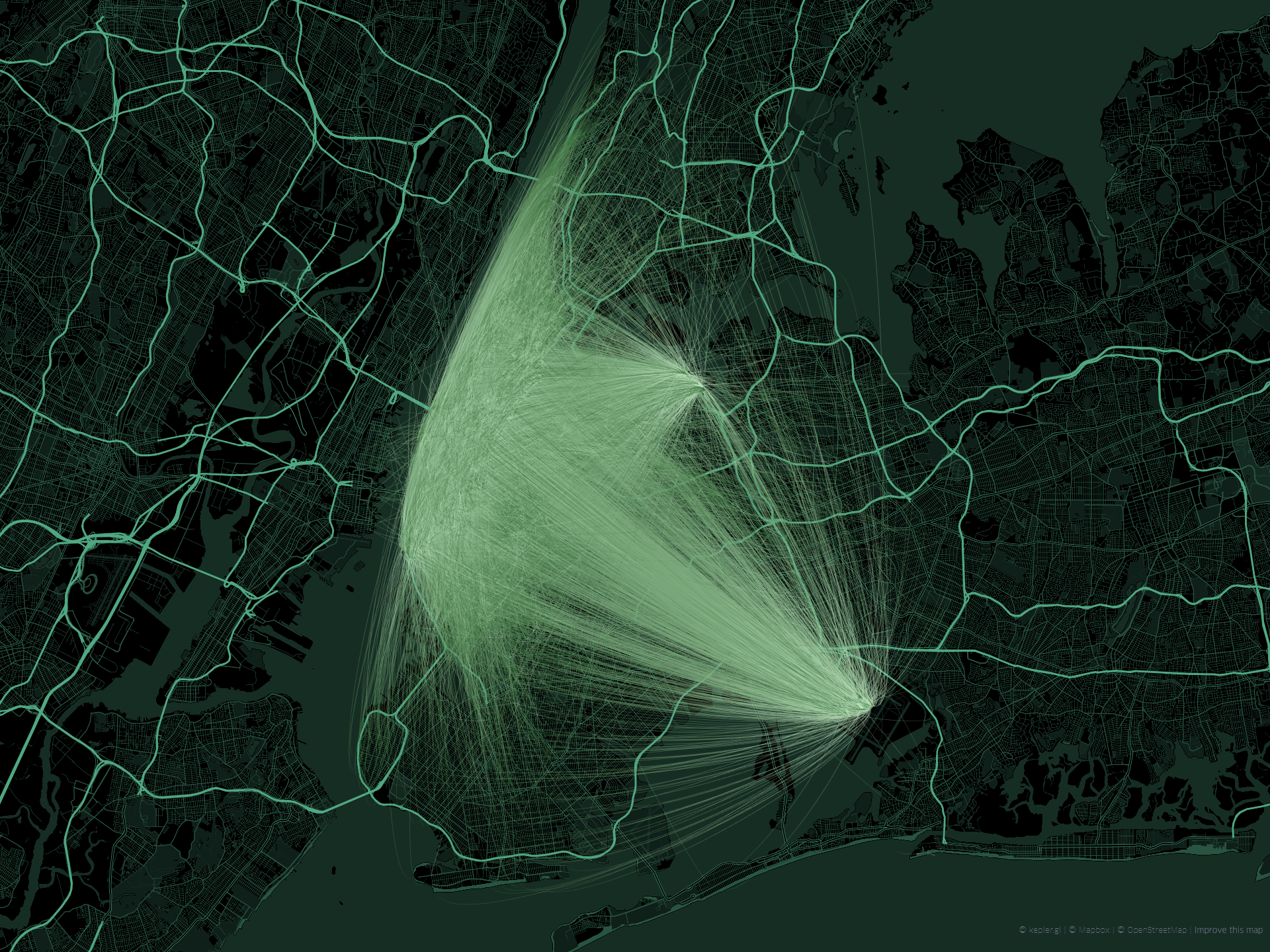图1

　　但这种传统的表达方式局限很明显：当OD记录数量众多时，因为不同线之间的彼此堆叠，导致很多区域之间的OD模式被遮盖而难以被读出。

　　而前一段时间我在观看一场学术直播的过程中，注意到一种特别的表达区域间OD数据的方式，原始文献比较老（ https://openaccess.city.ac.uk/id/eprint/537/1/wood_visualization_2010.pdf ）发表于2010年，其思想是通过对研究区域进行网格化划分，再将整个区域的原始网格映射到每个单一网格中：

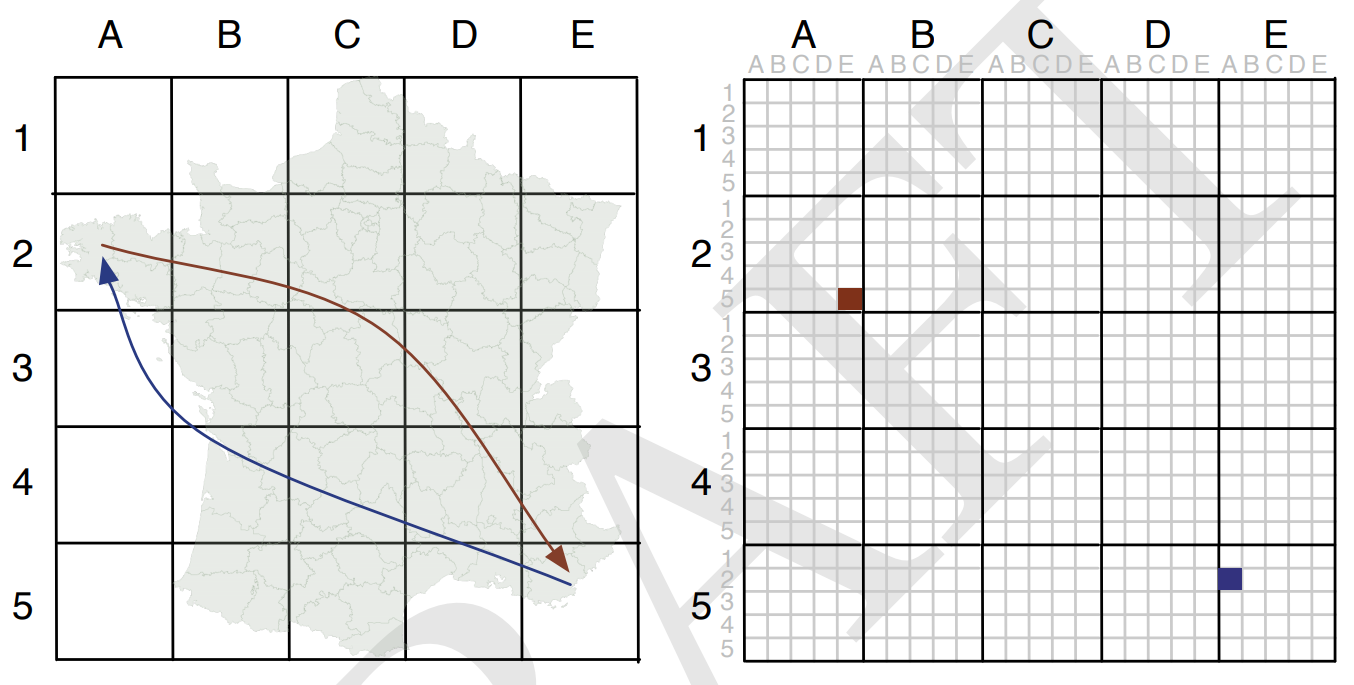图2

　　譬如图2左图中从坐标记为\((E, 5)\)的网格出发，到达记为\((A, 2)\)的网格的所有OD数据记录，可以在右图中对应左图\((E, 5)\)位置的大网格中，划分出的对应\((A, 2)\)相对位置的小网格中进行记录。

　　通过这样的方式，原始文献将图3所示原始OD线图转换为图4：

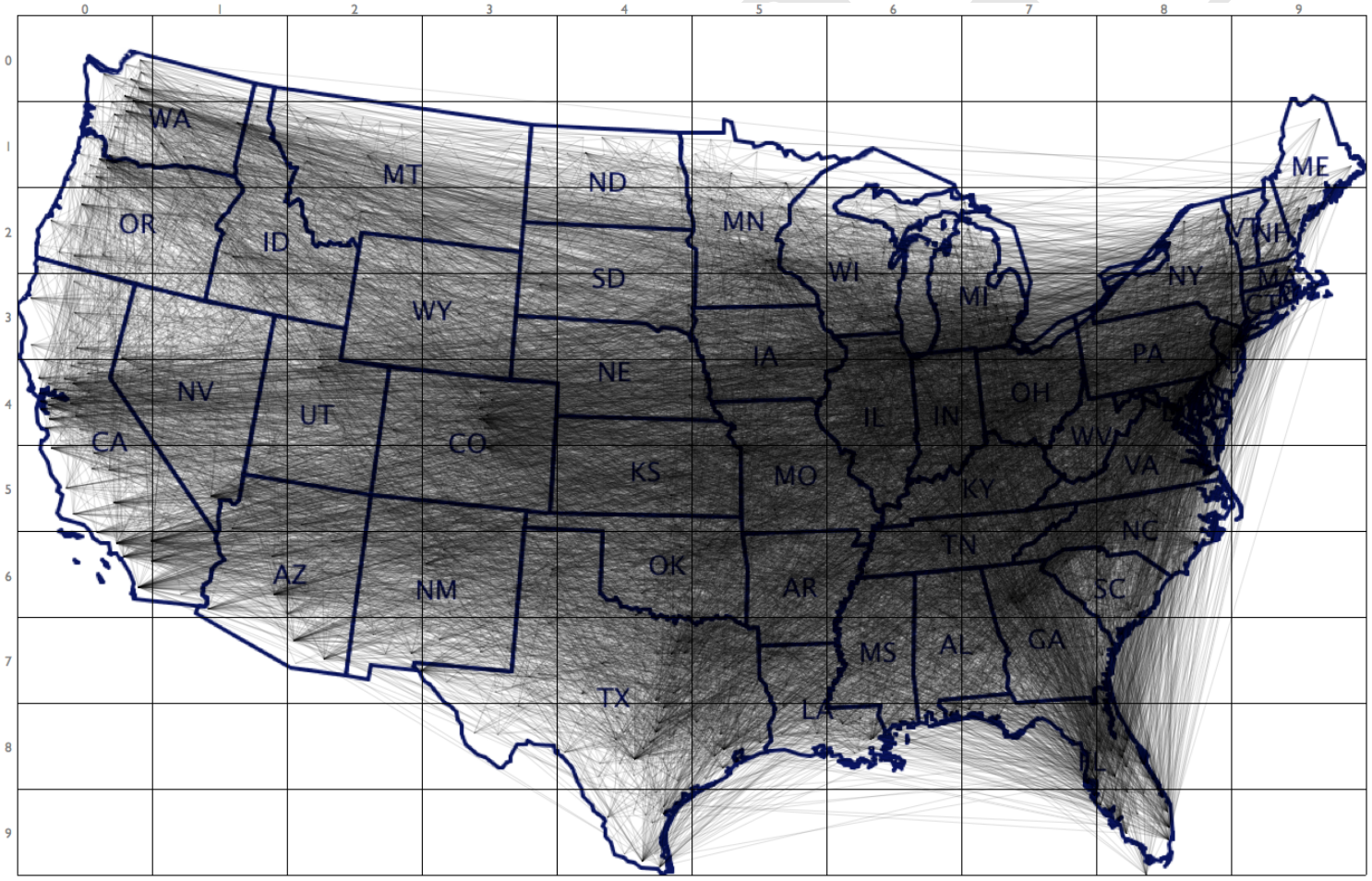图3
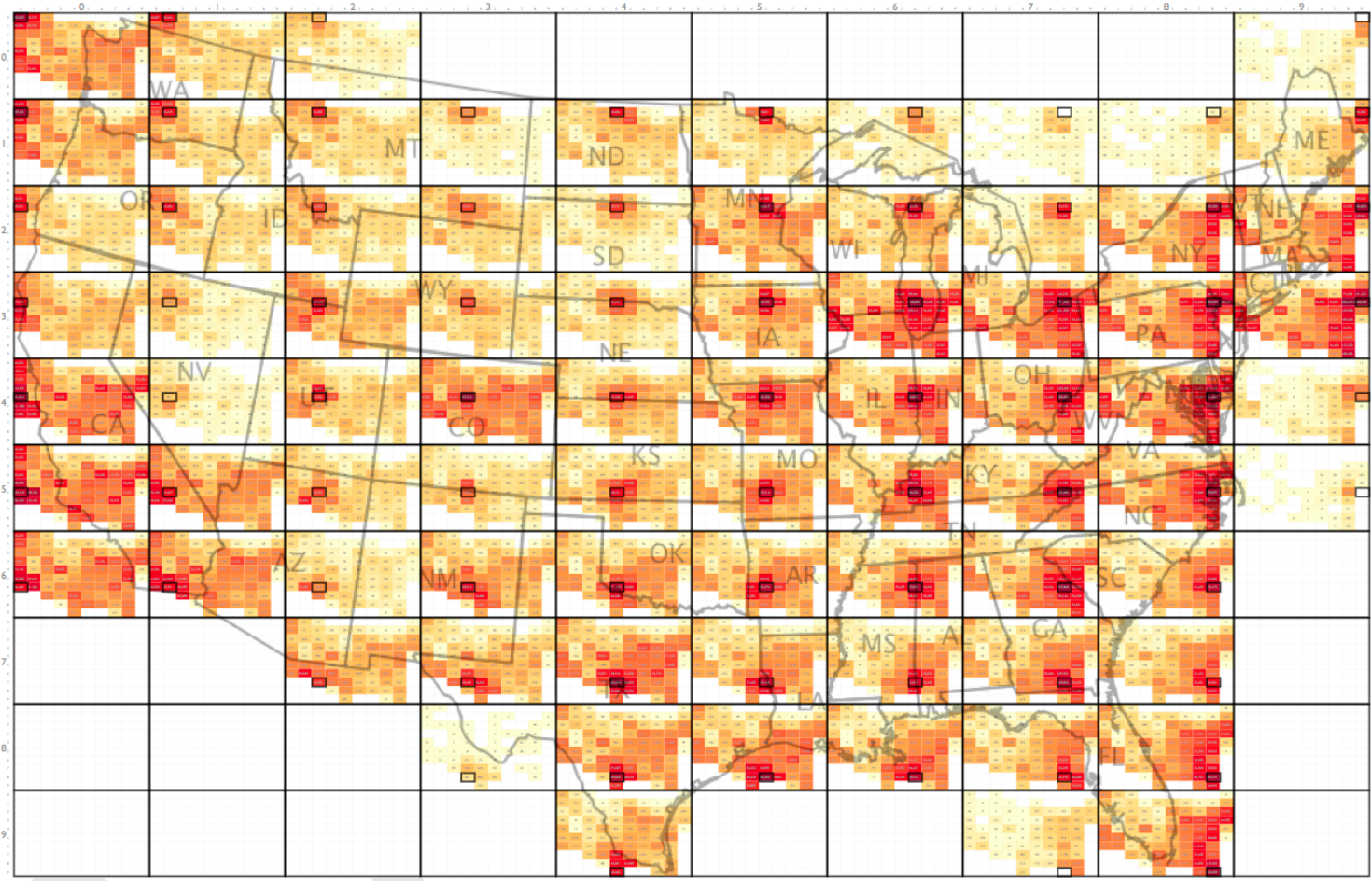图4

　　使得我们可以非常清楚地观察到每个网格区域对其他网格区域的OD模式，而本文就将利用Python，在图1对应的Uber上下车点分布数据的基础上，实践这种表达OD数据的特别方式。

2 模仿过程

2.1 过程分解

　　首先我们需要梳理一下整体的逻辑，先来看看原始的数据：

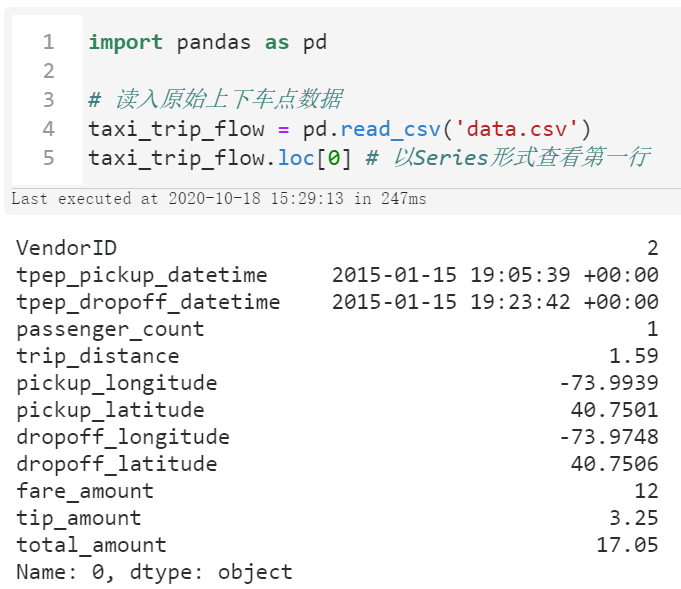图5

　　可以看到，原始数据中我们在本文真正用得到字段为上车点经纬度pickup_longitude与pickup_latitude，以及下车点经纬度dropoff_longitude与dropoff_latitude。

　　我的思路是首先对所有经纬度点进行去重，接着保存为GeoDataFrame并统一坐标参考系为Web墨卡托也就是EPSG:3857：

from shapely.geometry import Point
import geopandas as gpd

od_points = \
(
    # 首先合并所有的经纬度信息
    pd
    .concat([taxi_trip_flow[['pickup_longitude', 'pickup_latitude']]
             .rename(columns={'pickup_longitude': 'lng',
                              'pickup_latitude': 'lat'}),
             taxi_trip_flow[['dropoff_longitude', 'dropoff_latitude']]
             .rename(columns={'dropoff_longitude': 'lng',
                              'dropoff_latitude': 'lat'})])
    # 对经纬度进行去重
    .drop_duplicates()
)

# 基于经纬度信息为od_points添加矢量信息列
od_points['geometry'] = (
    od_points
    .apply(lambda row: Point(row['lng'], row['lat']), axis=1)
)

# 转换为GeoDataFrame并统一坐标到Web墨卡托
od_points = gpd.GeoDataFrame(od_points, crs='EPSG:4326').to_crs('EPSG:3857')

od_points.head()

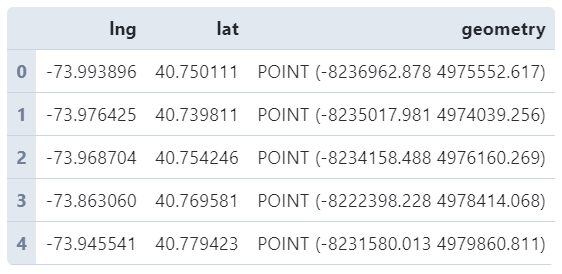图6

　　接下来我们来为研究区域创建网格面矢量数据，思路是利用numpy先创建出x和y方向上的等间距坐标，譬如我们这里创建5行5列：

from shapely.geometry import MultiLineString
from shapely.ops import polygonize # 用于将交叉线转换为网格面

# 提取所有上下车坐标点范围的左下角及右上角坐标信息
xmin, ymin, xmax, ymax = od_points.total_bounds

# 创建x方向上的所有坐标位置
x = np.linspace(xmin,
                xmax,
                6)

# 创建y方向上的所有坐标位置
y = np.linspace(ymin,
                ymax,
                6)

　　再利用双层列表推导配合MultiLineString生成彼此交叉的网格线，并利用shapely中提供的polygonize工具直接把交叉线转换为MultiPolygon，再拆分每个单一网格并添加一一对应的id信息以方便之后的分析过程。

# 生成全部交叉线坐标信息
hlines = [((x1, yi), (x2, yi)) for x1, x2 in zip(x[:-1], x[1:]) for yi in y]
vlines = [((xi, y1), (xi, y2)) for y1, y2 in zip(y[:-1], y[1:]) for xi in x]

# 创建网格
manhattan_grids = gpd.GeoDataFrame({
    'geometry': list(polygonize(MultiLineString(hlines + vlines)))},
    crs='EPSG:3857')

# 添加一一对应得id信息
manhattan_grids['id'] = manhattan_grids.index

　　上面的创建网格的方法非常实用，爱学习的朋友的可以仔细看懂之后记录下来。

　　我们来简单看看创建出的网格是什么样子的，配合contextily添加上在线底图：

import matplotlib.pyplot as plt
import contextily as ctx

fig, ax = plt.subplots(figsize=(4, 4), dpi=200)
ax = manhattan_grids.plot(facecolor='none', edgecolor='black', ax=ax)

# 标注每个网格的id
for row in manhattan_grids.itertuples():

    centroid = row.geometry.centroid
    ax.text(centroid.x, centroid.y, row.id, ha='center', va='center')

# 关闭坐标轴
ax.axis('off')

# 添加carto的素色底图
ctx.add_basemap(ax,
                source='https://d.basemaps.cartocdn.com/light_nolabels/{z}/{x}/{y}.png',
                zoom=12)

fig.savefig('图7.png', dpi=300, bbox_inches='tight', pad_inches=0)

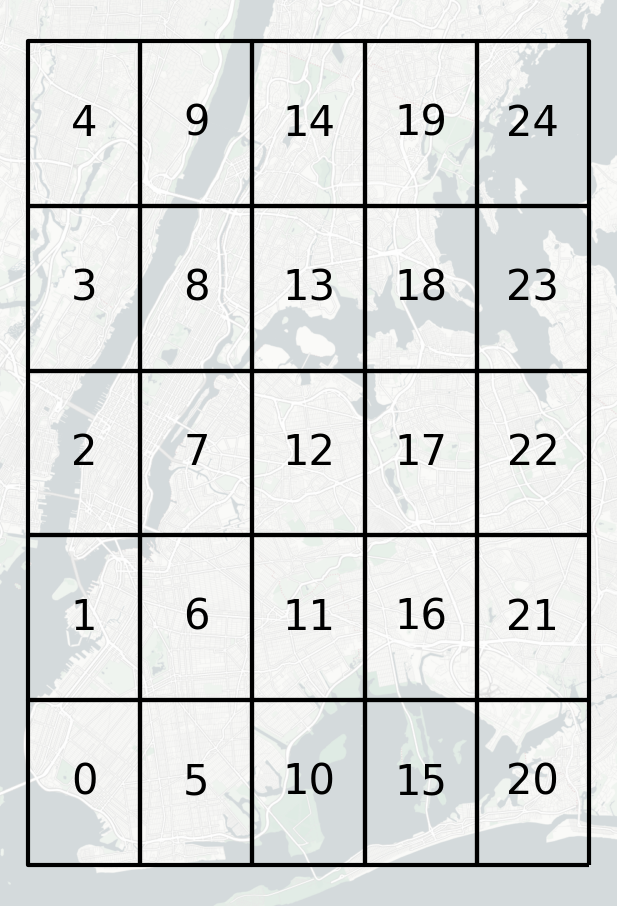图7

　　创建出的网格效果不错~接下来就到了最关键的地方，我们需要计算出在每个原始网格内部上车的全部OD记录，在整个区域中各个网格内的下车点分布情况：

　　首先我们以某个网格为例，介绍如何为其关联上车点、下车点以信息，并利用简单的仿射变换得到镶嵌在其内部的小网格。

　　以id=21的网格为例，对应着肯尼迪国际机场的区域，首先我们利用id对应的从manhattan_grids表中提取的网格面数据，基于空间连接来与od_points表进行关联，从而匹配到目标网格内对应原始od信息表中的所有上车点记录；

　　接着根据这些记录对应的下车点信息与od_points表进行匹配，从而得到所有下车点矢量信息，然后再次利用空间连接，得到所需的网格下车点分布结果：

i = 21 # 对应肯尼迪国际机场的网格

# 计算得到所有网格整体的重心坐标
center_grid = (manhattan_grids.unary_union.centroid.x,
               manhattan_grids.unary_union.centroid.y)

# 提取对应下车点坐标
dropoff = (
    # 利用空间连接，提取目标网格中包含到的所有坐标点
    gpd
    .sjoin(manhattan_grids.loc[i:i, :],
           right_df=od_points,
           op='contains')
    [['lng', 'lat', 'geometry']]
    # 利用提取到的坐标点信息，关联在目标
    # 网格中上车的记录对应的下车点坐标
    .merge(taxi_trip_flow[['pickup_longitude',
                           'pickup_latitude',
                           'dropoff_longitude',
                           'dropoff_latitude']],
           left_on=['lng', 'lat'],
           right_on=['pickup_longitude',
                     'pickup_latitude'])
    [['dropoff_longitude', 'dropoff_latitude']]
    # 根据匹配到的下车点坐标
    # 与od_points表进行连接
    # 找到对应下车点的矢量信息
    .merge(od_points,
           left_on=['dropoff_longitude', 'dropoff_latitude'],
           right_on=['lng', 'lat'])[['geometry']]
)

# 提取上一步得到的下车坐标点在各个网格中的分布数据
grid_distrib = (
    # 利用空间连接匹配网格与下车坐标点
    gpd
    .sjoin(manhattan_grids,
           # 转换为同一坐标参考系的GeoDataFrame
           gpd.GeoDataFrame(dropoff, crs='EPSG:3857'),
           op='contains')
    # 根据网格id进行分组计数
    .groupby('id', as_index=False)
    .agg({'index_right': 'count'})
    .rename(columns={'index_right': '下车记录数'})
)

grid_distrib.head()

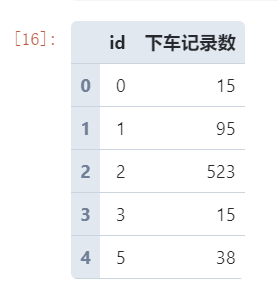图8

　　接着我们将上述的统计结果按照id列与原始网格表进行关联，并利用仿射变换得到整体网格向目标网格内部的缩小镶嵌结果（思路是首先将原始网格整体移动到与目标网格重心重合，接着按照x和y方向上的比例进行缩小），为了方便之后绘图标记出目标网格对应的镶嵌小网格位置，最后还需添加是否为目标网格列信息：

# 利用基本的仿射变换得到原始网格向对应目标网格的嵌入变换

# 获取当前目标网格的重心坐标
center_child_grid = (manhattan_grids.at[i, 'geometry'].centroid.x,
                     manhattan_grids.at[i, 'geometry'].centroid.y)

# 利用仿射变换得到整体网格在目标网格中的镶嵌
draw_gdf = (
    manhattan_grids
    # 基于原始的网格矢量来更新放缩后的网格矢量
    .assign(geometry=manhattan_grids
            # 第一步：将原始网格的重心平移到目标网格的重心上
            .translate(center_child_grid[0]-center_grid[0],
                       center_child_grid[1]-center_grid[1])
            # 第二步：以目标网格的重心为缩放中心，进行
            .scale(xfact=1 / 5, yfact=1 / 5,
                   origin=(manhattan_grids.at[i, 'geometry'].centroid.x,
                           manhattan_grids.at[i, 'geometry'].centroid.y)))
    .merge(grid_distrib, on='id', how='left')
    .assign(是否为目标网格=0)
)

draw_gdf.loc[draw_gdf.id == i, '是否为目标网格'] = 1
draw_gdf.head()

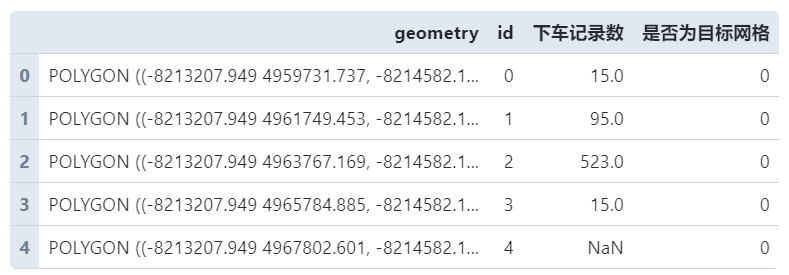图9

　　经过这一系列操作，我们就得到了id为21的网格下车点分布结果，将上述过程利用循环推广到每个网格，并将最后的计算结果合并为一张GeoDataFrame，即表draw_base。

2.2 绘制图像

　　最终我们对draw_base表进行可视化，这里为了显示更加自然，对下车记录进行了对数化+自然间断处理：

%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 12))

# 绘制每个镶嵌小网格的轮廓
ax = (
    draw_base
    .plot(facecolor='none', edgecolor='lightgrey', ax=ax,
          linewidth=0.3)
)

# 绘制每个镶嵌小网格的下车记录数热力分布
ax = (
    draw_base
    .assign(下车记录数=np.log(draw_base.下车记录数))
    .plot(column='下车记录数', scheme='NaturalBreaks',
          k=5, cmap='YlOrRd', ax=ax, alpha=0.7)
)

# 绘制原始网格的框架
ax = manhattan_grids.plot(ax=ax, facecolor='none', edgecolor='black',
                          linewidth=0.8)

# 在每个原始网格中标记出对应位置的镶嵌小网格
ax = (
    draw_base
    .query('是否为目标网格 == 1')
    .plot(facecolor='none', edgecolor='black',
          linestyle='--', ax=ax)
)

# 设置绘图区域范围
minx, miny, maxx, maxy = manhattan_grids.total_bounds
ax.set_xlim(minx, maxx)
ax.set_ylim(miny, maxy)

# 关闭坐标轴
ax.axis('off')

# 添加在线底图
ctx.add_basemap(ax,
                source='https://d.basemaps.cartocdn.com/light_nolabels/{z}/{x}/{y}.png',
                zoom=12)

# 保存图像
fig.savefig('图10.png', dpi=500, bbox_inches='tight', pad_inches=0)

图10

　　通过这种表达方式，我们可以很明显地看出不同区域相对其他区域出行模式的不同，你还可以根据自己的需要，对上述绘图逻辑进行调整，譬如每个原始网格内部色彩独立映射等。

---

　　以上就是本文的全部内容，欢迎在评论区与我进行讨论~