校内测试：T1秋末的落叶（命题人gxl）官方题解

秋末的落叶 题解

传送门：https://www.luogu.com.cn/problem/U121886

Part 1：疏通题意

首先，我们从题意和样例解释中很容易提取到以下信息：

\(1、\)本题是一个图论题，\(maple[i]\)是第\(i\)个节点的点权，违和感则可以抽象成无向边的边权

\(2、\)如果一条边连接的两个端点都在所选中的子图中，那么这条边也必须在子图中

\(3、\)题目所求：找到一个连通子图使得点权和除以边权和最大（在以下数学证明中，我们用\(t\)表示这个值）

Part 2：数学证明

首先已经告诉大家这是一个贪心题那就大大降低了这个题的难度

我们的任务简化为：找到一个贪心的办法（好像没啥实质性变化）

首先考虑图的两种基本形态：环状和链状

我们看看，环状的子图和链状的子图中，可不可以证明其中一种一定比另一种更优，这样我们的检索范围就会大大减小

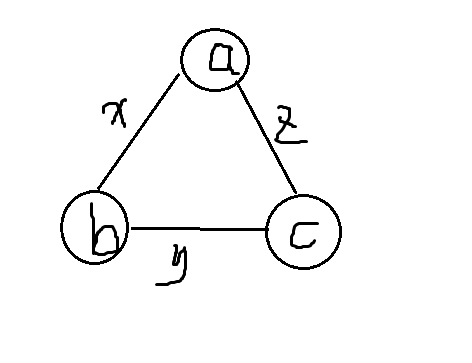
灵魂画师请见谅

开始证明：

那么在这个简单环中，我们设置以下四个变量来表示环和链的\(t\)值

用\(t_{abc}\)来表示环的\(t\)值，有\(t_{abc}=\frac{a+b+c}{x+y+z}\)

用\(t_{ab}\)表示两节点链\(ab\)的\(t\)值，有\(t_{ab}=\frac{a+b}{x}\)

用\(t_{bc}\)表示两节点链\(bc\)的\(t\)值，有\(t_{bc}=\frac{b+c}{y}\)

用\(t_{ac}\)表示两节点链链\(ac\)的\(t\)值，有\(t_{ac}=\frac{a+c}{z}\)

首先，不妨设\(t_{ab}\geq t_{bc}\geq t_{ac}\)，（PS：如果不满足，交换顺序即可，不影响证明的正确性）

那么化简\(t_{ab}，t_{bc}，t_{ac}\)得到了一个包含三个不等式的不等式组：

\(
\begin{cases}
ay+by\geq bx+cx\\
bz+cz\geq ay+cy\\
az+bz\geq ax+cx\\
\end{cases}
\)

因为 \(t_{ab}\geq t_{bc}\geq t_{ac}\)，只需要证明\(t_{ab}>t_{abc}\)，即可说明每一个环本身中，至少存在一个两节点链比这个环更优

左式：\(t_{ab}=\frac{a+b}{x}\)，右式：\(t_{abc}=\frac{a+b+c}{x+y+z}\)

\(1、\)同时乘以：\(x(x+y+z)\) 左式：\((a+b)(x+y+z)\)，右式：\(x(a+b+c)\)

\(2、\)同时减去：\(x(a+b)\) 左式：\((y+z)(a+b)\)，右式：\(cx\)

\(3、\)化简一步：左式：\(ay+by+az+bz\)，右式：\(cx\)

\(4、\)根据上面推出的不等式组：\(ay+by+az+bz\geq bx+cx+ax+cx=2cx+ax+bx\)

\(5、\)又因为：\(a、b、c、x、y、z\)均为正数，所以：\(2cx+ax+bx>cx\)

\(6、\)推出：左式\(>\)右式，即\(t_{ab}>t_{abc}\)

综上所述：每一个环本身中，至少存在一个两节点链比这个环更优

证毕

那么得到了这样一个结果——每一个环本身中，至少存在一个两节点链比这个环更优。现在，我们就不用考虑环的情况了

既然我们可以证明环和链之间的大小关系，进一步思考：链和链之间的大小关系可不可以证明呢？

让我们从最短的链证起，请看图：

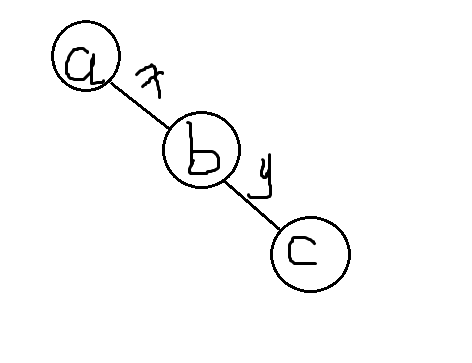
开始证明：

在这个三个节点组成的链中，我们设置以下三个变量来表示两个短链和一个长链的\(t\)值

用\(t_{abc}\)表示长链的\(t\)值，有\(t_{abc}=\frac{a+b+c}{x+y}\)

用\(t_{ab}\)表示短链\(ab\)的\(t\)值，有\(t_{ab}=\frac{a+b}{x}\)

用\(t_{bc}\)表示短链\(bc\)的\(t\)值，有\(t_{bc}=\frac{b+c}{y}\)

首先，不妨设：\(t_{ab}\geq t_{bc}\)（PS：如果不满足，依旧交换即可，不影响证明的正确性）

那么化简这个式子，得到一个不等式：\(ay+by\geq bx+cx\)

因为：\(t_{ab}\geq t_{bc}\)，只需证\(t_{ab}>t_{abc}\)，即可说明在任意一三节点个长链本身中，至少存在一个两节点短链比这个长链更优

左式：\(t_{ab}=\frac{a+b}{x}\)，右式：\(t_{abc}=\frac{a+b+c}{x+y}\)

\(1、\)同时乘以：\(x(x+y)\) 左式：\((a+b)(x+y)\)，右式：\(x(a+b+c)\)

\(2、\)同时减去：\(x(a+b)\) 左式：\(y(a+b)\)，右式：\(cx\)

\(3、\)化简一步：左式：\(ay+by\)，右式：\(cx\)

\(4、\)根据上面推出的不等式：\(ay+by\geq bx+cx\)，且\(x、y、a、b、c\)均为正数，有\(bx>0\)，所以推出\(ay+by>cx\)

\(5、\)推出：左式\(>\)右式，即\(t_{ab}>t_{abc}\)

综上所述：在任意一三节点个长链本身中，至少存在一个两节点短链比这个长链更优

（PS：感谢XMZ帮助我整理证明过程Orz）

但是还没有完，我们还需要得知长度为\(n\)的链和长度为\(2\)的链谁更优一些

\(n\)个节点链可以看成是\(n-1\)节点链和\(n\)节点链进行比较，而\(n-1\)又可以看成\(n-2\)节点链和\(n-1\)节点链比较

像上面这样一直进行递推下去，问题就又转化成了：三节点链和两节点链哪个更优这个问题，所以上面的证明方法对于无限长的链也都适用

根据沃兹基·施沃德（我自己说的）法则（应该是数学归纳法）可以把上面的证明推广到下面这个形式：

对于任意长度链，都在它本身中至少存在一个两节点链比它更优

证毕

Part 3：贪心思路

有了上面那么冗长的证明，我们终于归纳出了一个简单的结果：

答案一定是一个两节点构成的链

所以我们的贪心思路就是：找到一个\(t\)值最大的两节点链\(ab\)

妙啊！——zay

所以我们需要一个\(val\)数组，存放点权，每次输入三元组的时候，计算这个两节点链的\(t\)值，维护一个\(maxn\)最大即可

Part 4：代码实现

这个小学生都会吧……（所以这题是红题）

#include<bits/stdc++.h>
using namespace std;
double maxn,value[505];
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lf",&value[i]);
    for(int i=1,a,b;i<=m;i++){
        double c;
        scanf("%d%d%lf",&a,&b,&c);
        double k=(value[a]+value[b])/c;
        if(k>maxn) maxn=k;
    }
    printf("%.3lf\n",maxn);
    return 0;
}