运用sklearn进行线性判别分析(LDA)代码实现

基于sklearn的线性判别分析(LDA)代码实现

一、前言及回顾

本文记录使用sklearn库实现有监督的数据降维技术——线性判别分析（LDA）。在上一篇LDA线性判别分析原理及python应用（葡萄酒案例分析），我们通过详细的步骤理解LDA内部逻辑实现原理，能够更好地掌握线性判别分析的内部机制。当然，在以后项目数据处理，我们有更高效的实现方法，这篇将记录学习基于sklearn进行LDA数据降维，提高编码速度，而且会感觉更加简单。

LDA详细介绍与各步骤实现请看上回：LDA线性判别分析原理及python应用（葡萄酒案例分析）。

学习之后可以对数据降维处理两种实现方法进行对比：

1. 无监督的PCA技术：主成分分析PCA数据降维原理及python应用（葡萄酒案例分析）
2. 有监督的LDA技术：LDA线性判别分析原理及python应用（葡萄酒案例分析）

二、定义分类结果可视化函数

这个函数与上一篇文章 运用sklearn进行主成分分析(PCA)代码实现 里是一样的，plot_decision_region函数在分类结果区别决策区域中可以复用。

def plot_decision_regions(x, y, classifier, resolution=0.02):
    markers = ['s', 'x', 'o', '^', 'v']
    colors = ['r', 'g', 'b', 'gray', 'cyan']
    cmap = ListedColormap(colors[:len(np.unique(y))])

    x1_min, x1_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    x2_min, x2_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
    z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    z = z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)

    for idx, cc in enumerate(np.unique(y)):
        plt.scatter(x=x[y == cc, 0],
                    y=x[y == cc, 1],
                    alpha=0.6,
                    c=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx],
                    label=cc)

三、10行代码实现葡萄酒数据集分类

sklearn依然实现了LDA类方法，我们只需要直接调用而无需自己实现内部逻辑，这样显得更加方便。所以，10行代码实现也不为过，重点需要先理解内部逻辑原理。

关键代码如下：

lda = LDA(n_components=2)
lr = LogisticRegression()
x_train_lda = lda.fit_transform(x_train_std, y_train)  # LDA是有监督方法，需要用到标签
x_test_lda = lda.fit_transform(x_test_std, y_test)   # 预测时候特征向量正负问题，乘-1反转镜像
lr.fit(x_train_lda, y_train)
plot_decision_regions(x_train_pca, y_train, classifier=lr)
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend(loc='lower left')
plt.show()

使用训练集拟合模型之后，分类效果如何呢？

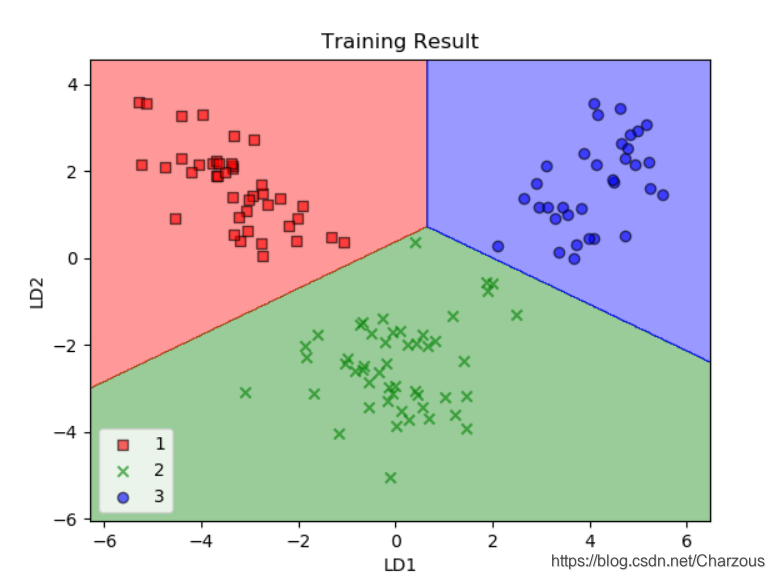
可以看到模型对训练数据集精确地分类，比PCA效果好，因为LDA使用了数据集的标签，是有监督的学习。

更准确来说，我们要看模型在测试集上的效果，对比如下：

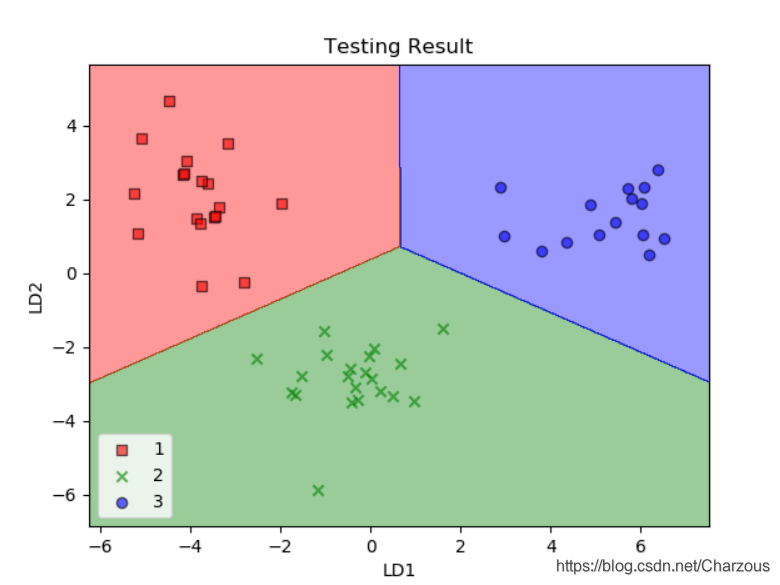
可见，经过逻辑回归分类器，提取了两个最具线性判别性的特征，将包含13个特征的葡萄酒数据集投影到二维子空间，实现了精确地分类。

四、完整代码

from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

def plot_decision_regions(x, y, classifier, resolution=0.02):
    markers = ['s', 'x', 'o', '^', 'v']
    colors = ['r', 'g', 'b', 'gray', 'cyan']
    cmap = ListedColormap(colors[:len(np.unique(y))])
    x1_min, x1_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    x2_min, x2_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
    z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    z = z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)

    for idx, cc in enumerate(np.unique(y)):
        plt.scatter(x=x[y == cc, 0],
                    y=x[y == cc, 1],
                    alpha=0.6,
                    c=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx],
                    label=cc)

def main():
    # load data
    df_wine = pd.read_csv('D:\\PyCharm_Project\\maching_learning\\wine_data\\wine.data', header=None)  # 本地加载
    # df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',
    #                       header=None)  # 服务器加载

    # split the data，train：test=7:3
    x, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, stratify=y, random_state=0)

    # standardize the feature 标准化单位方差
    sc = StandardScaler()
    x_train_std = sc.fit_transform(x_train)
    x_test_std = sc.fit_transform(x_test)

    lda = LDA(n_components=2)
    lr = LogisticRegression()
    x_train_lda = lda.fit_transform(x_train_std, y_train)  # LDA是有监督方法，需要用到标签
    x_test_lda = lda.fit_transform(x_test_std, y_test)  # 预测时候特征向量正负问题，乘-1反转镜像
    lr.fit(x_train_lda, y_train)
    plt.figure(figsize=(6, 7), dpi=100)  # 画图高宽，像素
    plt.subplot(2, 1, 1)
    plot_decision_regions(x_train_lda, y_train, classifier=lr)
    plt.title('Training Result')
    plt.xlabel('LD1')
    plt.ylabel('LD2')
    plt.legend(loc='lower left')

    plt.subplot(2, 1, 2)
    plot_decision_regions(x_test_lda, y_test, classifier=lr)
    plt.title('Testing Result')
    plt.xlabel('LD1')
    plt.ylabel('LD2')
    plt.legend(loc='lower left')
    plt.tight_layout()  # 子图间距
    plt.show()

if __name__ == '__main__':
    main()

五、降维压缩数据技术总结

至此，数据降维压缩的技术学习告一段落，经过这次学习，我感觉到一次比较系统的学习会收获更多，此次学习了主成分分析（PCA)和线性判别分析（LDA），这两种经典的数据降维技术各有特点。

前者是无监督技术，忽略分类标签，寻找最大化方差方向提取主成分；后者是有监督技术，训练时候考虑分类标签，在线性特征空间最大化类的可分性。应用场景也各有优势，PCA在图像识别应用好，LDA在特征提取方面更有优势。

这里列出这次学习过程的博文记录，方便查找：

1. 主成分分析PCA数据降维原理及python应用（葡萄酒案例分析）
2. 运用sklearn进行主成分分析(PCA)代码实现
3. LDA线性判别分析原理及python应用（葡萄酒案例分析）
4. 运用sklearn进行线性判别分析(LDA)代码实现

---

我的博客园：运用sklearn进行线性判别分析(LDA)代码实现

我的CSDN：https://blog.csdn.net/Charzous/article/details/108064317

版权声明：本文为博主原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/Charzous/article/details/108064317