图解算法——KMP算法

KMP算法

解决的是包,含问题。

Str1中是否包含str2，如果包含，则返回子串开始位置。否则返回-1。

示例1：

Str1:abcd123def

Str2:123d

暴力法：

从str1的第一个字二哥符开始依此匹配，当以第一个字符开头的子串匹配不上时，开始从第二个字符开始。缺点：每一次匹配都是互相独立的。

复杂度为O(N*M)，且N>=M。因为N<M就肯定不包含M长度的子串。

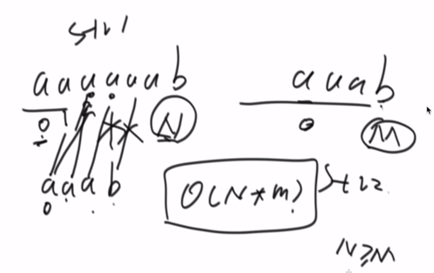
KMP算法将每一次的匹配进行了交涉。

此时，加入了字符串前后缀的概念。但要保证前后缀不能等于该字符串的长度。

以下分别以abcabcd和aaaaab字符串为例。

假设有这样的函数可以实现str2中每个位置的前面子串的最长前后缀。那么，

KMP算法的步骤就是：由原来的str1的i+1和str2的0匹配，改变为由str1的j和str2的0匹配，即由str1的x和str2的z匹配。如下图示：

举例说明：

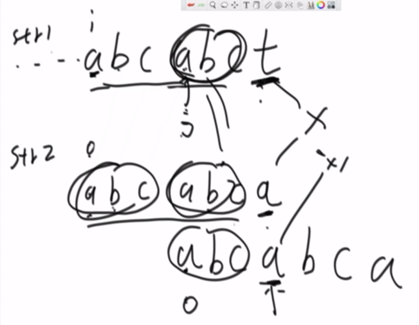
过程图解：

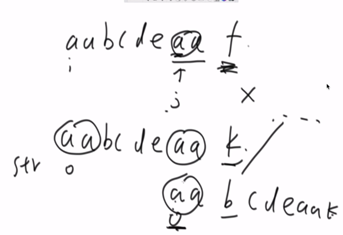
加速实质解析:  否定了从str1中的i+1位置到j-1位置能配出str2的可能性。

进一步解析：

假设从str1中的i+1位置到j-1位置中有一个k位置开始匹配能配出str2。

那么就会存在在str1的k位置开始有一个后缀串和str2的前缀串相等。但是这又是和最长前后串的概念相违背的。故不成立。

再举一个把str2两次后推的例子（一次匹配不成功）：

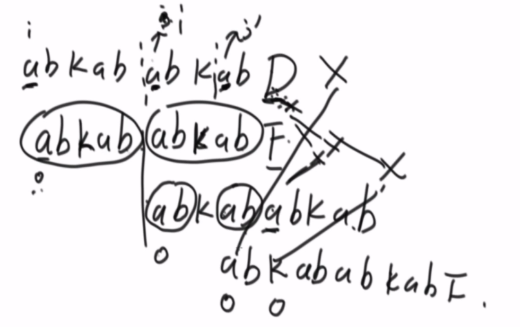
抽象出来就是：第一次匹配从str1的i开始和str2的0位置开始，匹配到最后到了甲指向的x位置和乙指向的Y位置，发现不匹配。则乙指向Y所对应的最长前后缀长度，即str2中位置指针乙回退到图示位置。下一步继续乙和甲（X）的下一个位置进行比较，这是为什么呢？因为两个画圈圈的部分是相等的，因为最长前后缀原理。

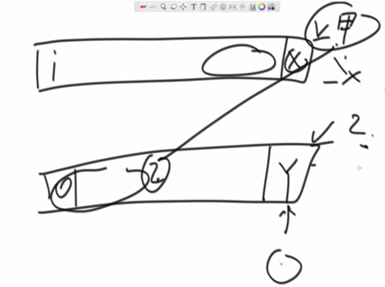
然后就是求解如何求得str2每个位置上的元素所对应的前面子串的最长前后缀位置。

原理如图：在0位置上设定为-1，1位置上设定为0，2位置上当0和1位置上相同时设定为1，否则设定为0。

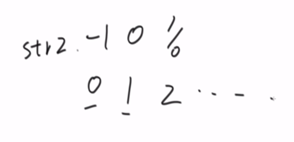
然后利用数学归纳法：求i位置上的索引长度。假设i-1位置上索引长度是4，则看位置为4的下一位，也就是位置为5的位置上（前缀的下一个字符）和i-1位置上的字符是否相等，如果相等，则i位置上的索引长度就是i位置上索引长度+1，即4+1=5。

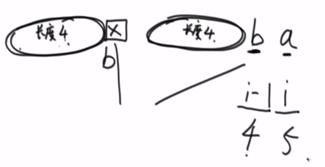
再举一例：

如果i-1位置上的索引长度4所对应的位置上的元素c和i-1位置上的元素t是否相等，如果相等，则i位置上的元素k所对应的索引长度就是i-1位置上的索引长度+1,即是5。如果不相等，则比较i-1位置上的索引长度4所对应的位置上的元素c的索引长度对应的元素a和i-1位置上的元素t是否相等，如果相等，则i位置上的元素k所对应的索引长度就是元素a所在位置上的索引长度+1,即是1+1=2，否则继续比较直至到该位置上对应的索引长度为0或者-1。类似于递归，也是数学归纳，不断往前看，往前寻找。

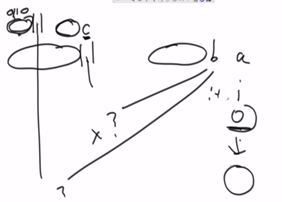
示例：

左侧是第一次比较c与t，第二次比较a与t都不对，a处已经对应的索引长度为0了，不能再继续向上寻找了，故i位置的k所对应的索引长度为0。

右图是第一次比较c与a，第二次比较a与a，匹配对了，此时c处对应的索引长度为2(ab)，故i位置的k所对应的索引长度为2+1=3。

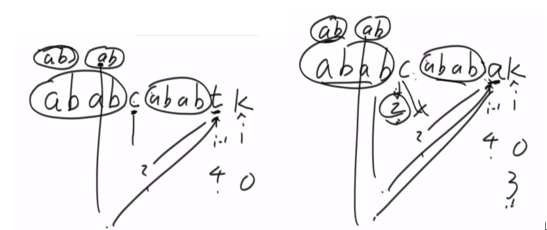
需要注意的是，永远和i-1位置上的元素去比较。直到比较相等，不相等就往前跳继续比较，直至到0。

代码如下：

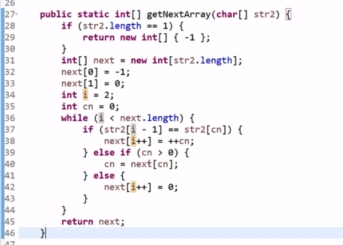
实战题目：

题目：

树的包含。

就是在左树T1是否包含右树T2。

思路：将树序列化成字符串（字符数组），要把NULL也加入，否则单纯先序中序是不行的。然后利用KMP算法。

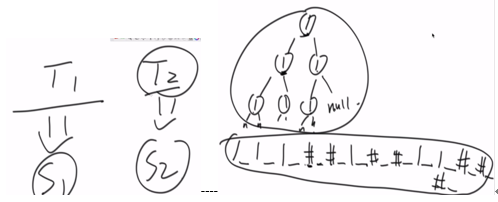
加入NULL的意义：

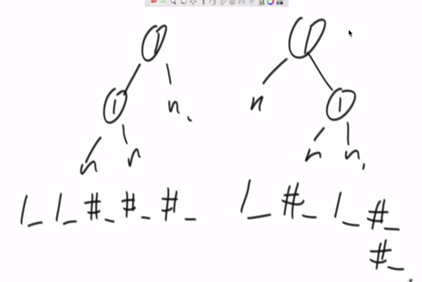
二题：

看一个串是否是范式得到的，如：abcabcabcabc，即是abc*n得到的。

该思路就是看每个字符的索引长度值是否是倍数关系。

Over......