NOIP 2018 D1 解题报告(Day

总分 205分

T1 100分

T2 95分

T3 10分

T1：

题目描述

春春是一名道路工程师，负责铺设一条长度为 nn 的道路。

铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 nn 块首尾相连的区域，一开始，第 ii 块区域下陷的深度为 d_idi 。

春春每天可以选择一段连续区间[L,R][L,R] ，填充这段区间中的每块区域，让其下陷深度减少 11。在选择区间时，需要保证，区间内的每块区域在填充前下陷深度均不为 00 。

春春希望你能帮他设计一种方案，可以在最短的时间内将整段道路的下陷深度都变为 00 。

输入格式

输入文件包含两行，第一行包含一个整数 nn，表示道路的长度。第二行包含 nn 个整数，相邻两数间用一个空格隔开，第ii 个整数为 d_idi 。

输出格式

输出文件仅包含一个整数，即最少需要多少天才能完成任务。

输入输出样例

输入 #1复制

6

4 3 2 5 3 5

输出 #1复制

说明/提示

【样例解释】

一种可行的最佳方案是，依次选择： [1,6][1,6]、[1,6][1,6]、[1,2][1,2]、[1,1][1,1]、[4,6][4,6]、[4,4][4,4]、[4,4][4,4]、[6,6][6,6]、[6,6][6,6]。

【数据规模与约定】

对于 30% 的数据，1 ≤ n ≤ 10，1≤n≤10 ；
对于 70% 的数据，1 ≤ n ≤ 10001≤n≤1000 ；
对于 100% 的数据，1 ≤ n ≤ 100000 , 0 ≤ d_i ≤ 100001≤n≤100000,0≤di≤10000 。

对于这个题来说，我其实一开始并不知道正解；然后我暴力A掉（数据的良心所在）

暴力思路：

现在对于一个坑，我们要去填平它，那么我们先看一下是否有地方已经被填平了，如果是的话，那么我们就填它两边的就行了，对于任意的一次填土，肯定是覆盖的区间越多越优，所以对于区间内没有被填平我们全部填上最靠近地面的那一个，也就是最小值；

复杂度：O(log(n))随机数据

/*thanks for gods*/

#include <iostream>

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <cmath>

#include <queue>

#define inf 0x3f

using namespace std;

const int maxn=2e5+10;

inline int read()

{

    int x=0,f=1;char ch=getchar();

    while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}

    while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}

    return x*f;

}

int n,d[maxn];

long long ans=0;

void devide(int l,int r)

{

    int end=0,pos=0,minn=10000,pos1;

    for(int i=l;i<=r;i++)

    {

        if(d[i]==0)

        {

            pos=i;

            end++;

        }

        if(minn>d[i])

        {

            minn=d[i],pos1=i;

        }

    }

    if(end==r-l+1) return ;

    if(!pos)

    {

        for(int i=l;i<=r;i++)

        {

            d[i]-=minn;

        }

        ans+=minn;

        pos=pos1;

    }

    devide(l,pos-1);

    devide(pos+1,r);

}

int main()

{

    //freopen("road.in","r",stdin);

    //freopen("road.out","w",stdout);

    n=read();

    for(int i=1;i<=n;i++)

    d[i]=read();

    devide(1,n);

    printf("%d",ans);

    return 0;

}

然后我抱着忐忑的心态，我认为拿到70分，结果A掉了

接下来就是正解思路：

正解的思路也是差不了多少，也就是在一个坑中，如果是一个下降的数列，那么我们就填平，如果是上升的数列，那么对于上升的每一层数来说，一定已经被填平；枚举就OK了，

复杂度： O（n）

发现，我的好像更快

T2：

在网友的国度中共有种不同面额的货币，第种货币的面额为，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为、面额数组为的货币系统记作。

在一个完善的货币系统中，每一个非负整数的金额都应该可以被表示出，即对每一个非负整数，都存在个非负整数满足的和为。然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额不能被该货币系统表示出。例如在货币系统 , 中，金额就无法被表示出来。

两个货币系统和是等价的，当且仅当对于任意非负整数，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统，满足与原来的货币系统等价，且尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的。

输入格式

输入文件名为 money.in。
输入文件的第一行包含一个整数，表示数据的组数。
接下来按照如下格式分别给出组数据。每组数据的第一行包含一个正整数。接下来一行包含个由空格隔开的正整数。

输出格式

输出文件名为 money.out。
输出文件共有行，对于每组数据，输出一行一个正整数，表示所有与等价的货币系统中，最小的。

样例

样例输入

2

4

3 19 10 6

5

11 29 13 19 17

样例输出

2

5

样例解释

在第一组数据中，货币系统和给出的货币系统等价，并可以验证不存在的等价的货币系统，因此答案为。

在第二组数据中，可以验证不存在的等价的货币系统，因此答案为。

数据范围与提示

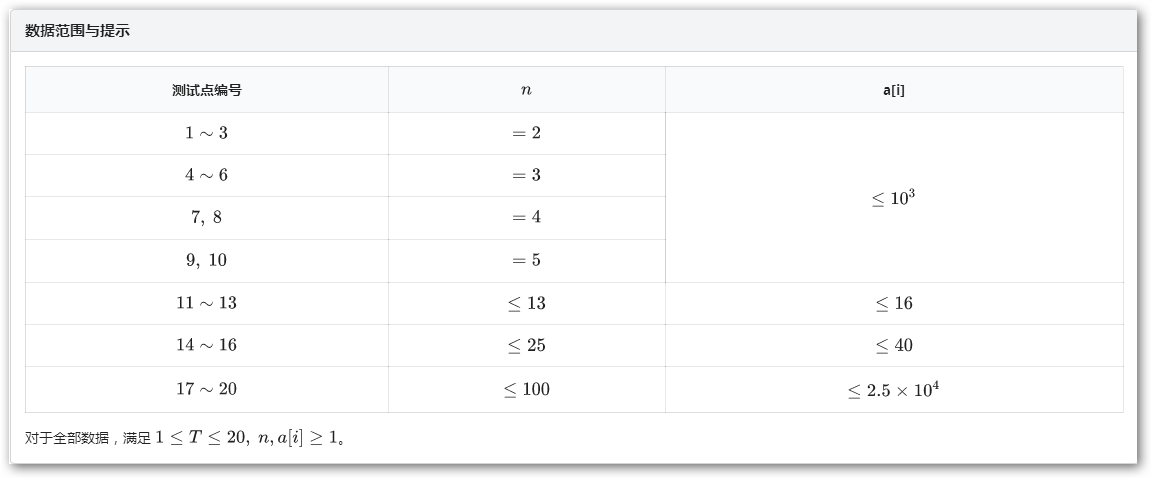
对于全部数据，满足。

解题思路：

对于这个题来说，我们要求从总货币系统（集合A）中求出一个货币系统（集合B），表示的数一样，且总数最小的，那么就很显然，B⊆A ；

那么我们的集合B中的任意一个元素，它只要能表示出A来，也就OK了，然后再注意看一下题面，无限张，那么很显然，我们就利用完全背包的思想就可以了，（不是多重背包，01背包是可以表示成完全背包的，而且这里也只是借用了完全背包的思想），那么，我们就设一个bool数组，f*

如果，f [ i ]为真，那么就意味着 i这个数可以被我们所选的货币系统也就是集合B表示出来，如果不是，那么我们把这个数加入到集合B中来，

同时，对于判断 f [ i ] 是否为真，

这里先说一个结论，也是十分显而易见：对于一个数 i ,因为这个钱，money,好东西，不能减，所以i就要被比i小的数字的和表示出来，

所以说，先排序;!!!!!!!!!!!!!!!!

所以枚举比 i小的数据，如果能凑出来，那么 i 减去这个数据能够凑出来，那么i 也一定能凑出来，所以状态转移方程也就是

：

　　　　f [ i ] = f [ i ] | f [ j - a [ i ] ]

也可以写成：

　　　　　　　　if ( f [ j - a [ i ] ] )　　f [ j ] = 1 ;

然后就可以愉快的AC了，当时我讲的时候，我着实不知道咋讲。。QwQ

代码：

#include <bits/stdc++.h>

using namespace std;

int f[25000];

int a[200];

int mx=0;

inline int read()

{

    int x=0,f=1;char ch=getchar();

    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}

    while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}

    return x*f;

}

int main()

{

    freopen("money.in","r",stdin);

    freopen("money.out","w",stdout);

    int i,j,n,t,ans;

    t=read();

    while(t--)

    {

        ans=0;

        memset(f,0,sizeof(f));

        n=read();

        for(i=1;i<=n;i++)

        {

        a[i]=read();

        mx=max(mx,a[i]);

        }

        sort(a+1,a+n+1);

        f[0]=1;

        for(i=1;i<=n;i++)

        {

            if(f[a[i]])

            {

                continue;

            }

            ans++;

            for(j=a[i];j<=mx;j++)

            {

                if(f[j-a[i]])

                {

                    f[j]=1;

                }

            }

        }

        printf("%d\n",ans);

    }

    return 0;

}

这个题数据很很很良心，然后我骗了10分，

C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建条赛道。

C 城一共有个路口，这些路口编号为，有条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第条道路连接的两个路口编号为和，该道路的长度为。借助这条道路，从任何一个路口出发都能到达其他所有的路口。

一条赛道是一组互不相同的道路，满足可以从某个路口出发，依次经过道路（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。

目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的条赛道中长度最小的赛道长度最大（即条赛道中最短赛道的长度尽可能大）。

输入格式

输入文件名为 track.in。
输入文件第一行包含两个由空格分隔的正整数，分别表示路口数及需要修建的赛道数。
接下来行，第行包含三个正整数，表示第条适合于修建赛道的道路连接的两个路口编号及道路长度。保证任意两个路口均可通过这条道路相互到达。每行中相邻两数之间均由一个空格分隔。

输出格式

输出文件名为 track.out。
输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

样例

样例输入 1

样例输出 1

样例解释 1

所有路口及适合于修建赛道的道路如下图所示：

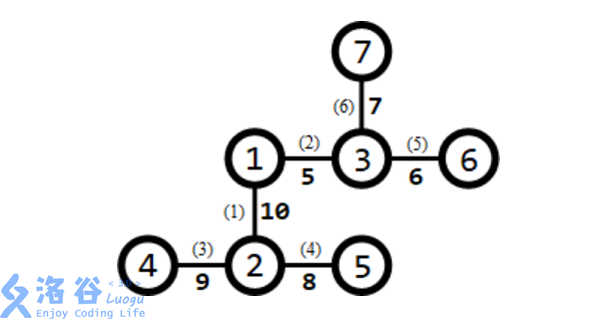
道路旁括号内的数字表示道路的编号，非括号内的数字表示道路长度。

需要修建条赛道。可以修建经过第条道路的赛道（从路口到路口），则该赛道的长度为，为所有方案中的最大值。

样例输入 2

样例输出 2

样例解释 2

所有路口及适合于修建赛道的道路如下图所示：

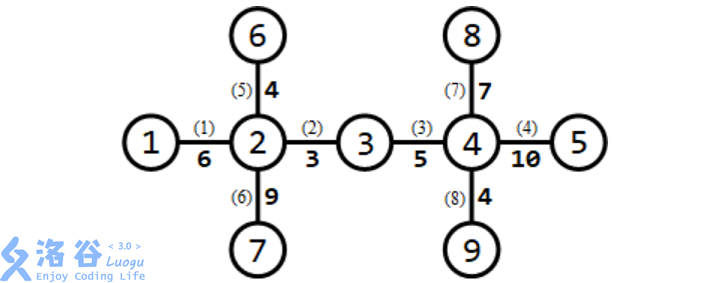
需要修建条赛道。可以修建如下条赛道：

经过第条道路的赛道（从路口到路口），长度为；
经过第条道路的赛道（从路口到路口），长度为；
经过第条道路的赛道（从路口到路口），长度为。

长度最小的赛道长度为，为所有方案中的最大值。

数据规模与约定

这数据真好看，不是，这姑娘真良心

所有测试数据的范围和特点如下表所示 :

其中，「分支不超过 33」的含义为：每个路口至多有 3 条道路与其相连。

对于所有的数据，2≤n≤5×10000, 1≤m≤n−1, 1≤ai,bi≤n, 1≤li≤10000

关于 multiset参考于(https://blog.csdn.net/sodacoco/article/details/84798621) ---- 二喵君

与（https://blog.csdn.net/qq_40032278/article/details/81511494 ） -------------- L--辰缘--H

解题思路：

最大值最小，好，我们直接想到了二分，二分什么呢？——困扰了我整整40多分钟（我当时就剩下40分钟了,~~~~(>_<)~~~~）

要求 m 条赛道中长度最小的赛道长度最大，所以我们二分就是赛道的长度，我们要求的就是最小的赛道，，，，，，然后长度最大

所以，题意就化成了在一棵树上能否找出小于等于 k 的 m 条路径；（为了加深我的理解，毕竟刚理解，写的多一点）

在分路径的时候，也用到了贪心；就是如果现在形成的长度不足k,那我们去寻找路径的时候，去寻找最小的且没被选过的路径，以此来保证我们所分得的路径最多，用的就是multiset；

考虑一棵子树对全局答案的贡献，显然有两个方面。

是当前子树中能最多能找到的满足要求的路径条数；
是连到当前子树的根的路径的长度。

这样也就可以求树的直径，不求树的直径也就是慢了300ms左右吧

然后，客官，上代码吧：

#include <iostream>

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <cmath>

#include <queue>

#include <set>

using namespace std;

const int maxn=50000+120;

struct node

{

    int nxt ,to,weath;

}edge[maxn<<1];

multiset<int> s[maxn];

multiset<int>::iterator it;

int dist,n,m,up;

inline int read()

{

    int x=0,f=1;char ch=getchar();

    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}

    while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}

    return x*f;

}

int number_edge,head[maxn<<1];

void add_edge(int from,int to,int weath)

{

    number_edge++;

    edge[number_edge].nxt=head[from];

    edge[number_edge].to=to;

    edge[number_edge].weath=weath;

    head[from]=number_edge;

}

int dfs1(int x,int fa

{

    int sum1=0;

    int sum2=0;

    for(int i=head[x];i;i=edge[i].nxt)

    {

        if(edge[i].to==fa)

        {

            continue;

        }

        sum2=max(sum2,dfs1(edge[i].to,x)+edge[i].weath);

        if(sum1<sum2)

        {

            swap(sum1,sum2);

        }

    }

    up=max(up,sum1+sum2);

    return sum1;

}

int dfs(int x,int fa,int k)

{

    s[x].clear();

    int val;

    for(int i=head[x];i;i=edge[i].nxt)

    {

        if(edge[i].to==fa)

        {

            continue;

        }

        val=dfs(edge[i].to,x,k)+edge[i].weath;

        if(val>=k)

        {

            dist++;

        }

        else

        {

            s[x].insert(val);

        }

    }

    int Max=0;

    while(!s[x].empty())

    {

        if(s[x].size()==1)

        {

            return max(Max,*s[x].begin());

        }

        it=s[x].lower_bound(k-*s[x].begin());

        if(it==s[x].begin()&&s[x].count(*it)==1)

        {

            it++;

        }

        if(it==s[x].end())

        {

            Max=max(Max,*s[x].begin());

            s[x].erase(s[x].find(*s[x].begin()));

        }

        else

        {

            dist++;

            s[x].erase(s[x].find(*it));

            s[x].erase(s[x].find(*s[x].begin()));

        }

    }

    return Max;

}

bool check(int k)

{

    dist=0;

    dfs(1,0,k);

    return dist>=m;

}

int main()

{

    n=read(),m=read();

    int ans;

    for(int i=1;i<=n-1;i++)

    {

        int x=read(),y=read(),w=read();

        add_edge(x,y,w);

        add_edge(y,x,w);

    }

    dfs1(1,0);

    int l=1,r=100000;

    while(l<r)

    {

        int    mid=l+r+1>>1;

        if(check(mid))

        {

            l=mid;

            ans=l;

        }

        else

        {

            r=mid-1;

        }

    }

    printf("%d\n",ans);

    return 0;

}

OK,综上所述，今天学到了着实不少~~To be continue;