H分形是由一个字母H演化出迷宫一样场景的分形图案，其构造过程是：取一个中心点（x,y），以此中心点绘制一条长为L的水平直线和两条长为H的竖直直线，构成一个字母“H”的形状；再以两条竖直直线的上下共4个端点为中心点，分别绘制一条长为L/2的水平直线和两条长为H/2的竖直直线；重复以上操作直至达到要求的层数，可以绘制出H分形图案，如图1所示。

图1  H分形图案的生成

H分形采用递归过程易于实现，编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>H分形</title>

</head>

<body>

<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

ctx.strokeStyle = "red";

ctx.lineWidth = 3;

var maxdepth =4;

var curdepth = 0;

function drawH(x,y,length,hight)

{

curdepth++;

ctx.beginPath();

ctx.moveTo(x-length/2,y);

ctx.lineTo(x+length/2,y);

ctx.moveTo(x-length/2,y-hight/2);

ctx.lineTo(x-length/2,y+hight/2);

ctx.moveTo(x+length/2,y-hight/2);

ctx.lineTo(x+length/2,y+hight/2);

ctx.stroke();

if(curdepth <= maxdepth)

{

drawH(x-length/2,y-hight/2,length*0.5,hight*0.5);

drawH(x-length/2,y+hight/2,length*0.5,hight*0.5);

drawH(x+length/2,y-hight/2,length*0.5,hight*0.5);

drawH(x+length/2,y+hight/2,length*0.5,hight*0.5);

}

curdepth--;

}

drawH(250,250,240,180);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出的H分形图案，如图2所示。

图2  递归深度maxdepth =4的H分形

将H分形的生成过程进行动态展示，编写如下的HTML文件。

<!DOCTYPE html>

<head>

<title>H分形</title>

</head>

<body>

<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

ctx.strokeStyle = "red";

ctx.lineWidth = 3;

var maxdepth =0;

var curdepth = 0;

function drawH(x,y,length,hight)

{

curdepth++;

ctx.beginPath();

ctx.moveTo(x-length/2,y);

ctx.lineTo(x+length/2,y);

ctx.moveTo(x-length/2,y-hight/2);

ctx.lineTo(x-length/2,y+hight/2);

ctx.moveTo(x+length/2,y-hight/2);

ctx.lineTo(x+length/2,y+hight/2);

ctx.stroke();

if(curdepth <= maxdepth)

{

drawH(x-length/2,y-hight/2,length*0.5,hight*0.5);

drawH(x-length/2,y+hight/2,length*0.5,hight*0.5);

drawH(x+length/2,y-hight/2,length*0.5,hight*0.5);

drawH(x+length/2,y+hight/2,length*0.5,hight*0.5);

}

curdepth--;

}

function go()

{

ctx.clearRect(0,0,canvas.width,canvas.height);

drawH(250,250,240,180);

maxdepth++;

curdepth=0;

if (maxdepth>4)

{

maxdepth=0;

}

}

window.setInterval('go()', 1500);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，在浏览器窗口中呈现出如图3所示的H分形动态生成效果。

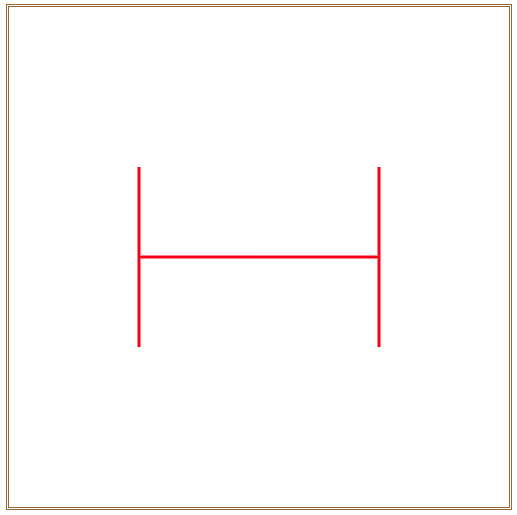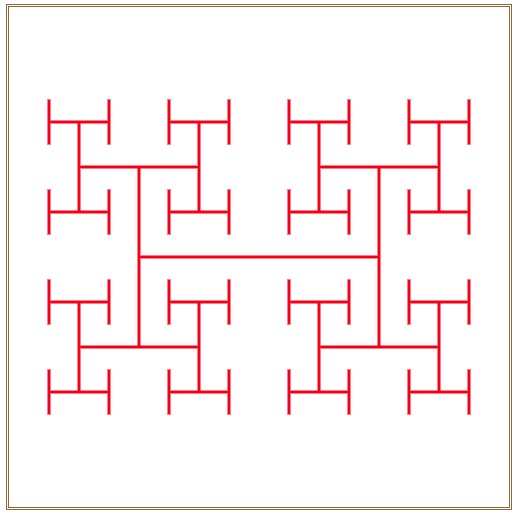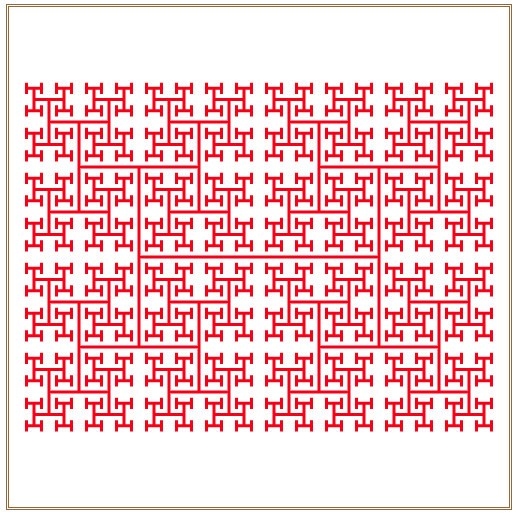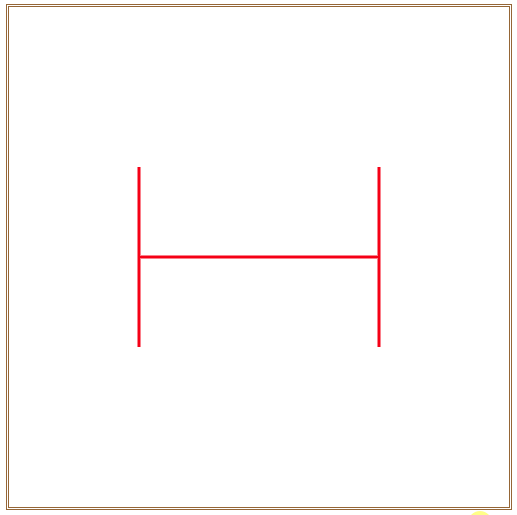
图3  H分形图案动态生成

JavaScript图形实例：H分形的更多相关文章

  1. JavaScript图形实例：再谈IFS生成图形

    在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...

  2. JavaScript图形实例：线段构图

    在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...

  3. JavaScript图形实例：随机SierPinski三角形

    在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...

  4. JavaScript图形实例：迭代函数系统生成图形

    迭代函数系统(Iterated Function System,IFS)可以用来创建分形图案,它是分形理论的重要分支,也是分形图形处理中最富生命力而且最具有广阔应用前景的领域之一.这一工作最早可以追溯 ...

  5. JavaScript图形实例：图形的旋转变换

    旋转变换:图形上的各点绕一固定点沿圆周路径作转动称为旋转变换.可用旋转角表示旋转量的大小. 旋转变换通常约定以逆时针方向为正方向.最简单的旋转变换是以坐标原点(0,0)为旋转中心,这时,平面上一点P( ...

  6. JavaScript图形实例：SierPinski三角形

    1．SierPinski三角形 Sierpinski三角形是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集.其生成过程为: (1)取一个三角形(多数使用等边三角形): (2) ...

  7. JavaScript图形实例：Hilbert曲线

    德国数学家David Hilbert在1891年构造了一种曲线,首先把一个正方形等分成四个小正方形,依次从西北角的正方形中心出发往南到西南正方形中心,再往东到东南角的正方形中心,再往北到东北角正方形中 ...

  8. JavaScript图形实例：Canvas API

    1．Canvas概述 Canvas API(画布)用于在网页实时生成图像,并且可以操作图像内容,基本上它是一个可以用JavaScript操作的位图(bitmap). 要使用HTML5在浏览器窗口中绘制 ...

  9. JavaScript图形实例：合成花卉图

    我们知道在直角坐标系中,圆的方程可描述为: X=R*COS(α) Y=R*SIN(α) 用循环依次取α值为0~2π,计算出X和Y,在canvas画布中将坐标点(X,Y)用线连起来,可绘制出一个圆.编写 ...

随机推荐

  1. 记一次Docker中Redis连接暴增的问题排查

    周六生产服务器出现redis服务器不可用状态,错误信息为: 状态不可用,等待后台检查程序恢复方可使用.Unexpected end of stream; expected type 'Status' ...

  2. 00-02.kaliLinux-配置SSH服务

    KaliLinux的SSH服务默认是需要手动配置好后才能使用,否则通过xShell等工具是无法连接上的. 修改SSH服务的配置文件 root@kali:~# cd /etc/ssh root@kali ...

  3. @luogu - P6109@ [Ynoi2009]rprmq

    目录 @description@ @solution@ @accepted code@ @details@ @description@ 有一个 n×n 的矩阵 a,初始全是 0,有 m 次修改操作和 ...

  4. matlab-整数规划(非线性规划之蒙特卡洛法（随机取样法）)

    首先编写M 文件mengte.m 定义目标函数f 和约束向量函数g,程序如下:function [f,g]=mengte(x);%定义目标函数f和约束向量函数g f=x()^+x()^+*x()^+* ...

  5. pip环境变量配置

    找到python安装目录,进入C:\Users\EDZ\AppData\Local\Programs\Python\Python37-32\Scripts  下.添加此地址到path中 打开cmd 输 ...

  6. 基于docker-compose部署jumpserver

    基于docker-compose部署jumpserver 组件说明 Jumpserver 为管理后台, 管理员可以通过 Web 页面进行资产管理.用户管理.资产授权等操作, 用户可以通过 Web 页面 ...

  7. MFC中窗口启动后，CEdit编辑框默认光标位置设置，顺序的调节方法

    MFC中窗口启动后,CEdit编辑框默认光标位设置,顺序的调节方法 在编辑界面按下ctrl+D键,就会出现所有控件的Tab键顺序,按照自己想要的顺序依次点击控件,就可以重新安排顺序.数值1就是默认停留 ...

  8. Java WebService学习笔记 - Axis(一)

    WebService 简介 实际开发中,很多系统都是基于历史遗留系统进行开发,有时,这些系统基于不同的语言,如C,C++,C#,java,PHP等等.为了实现历史系统的再利用,或向外部程序暴露调用接口 ...

  9. 03.基于测试开发讲解和Cobertura框架介绍

    首先我们先 CREATE TABLE `t_user` ( `id` int(11) NOT NULL AUTO_INCREMENT, `username` varchar(200) DEFAULT ...

  10. VulnHub CengBox2靶机渗透

    ​本文首发于微信公众号:VulnHub CengBox2靶机渗透,未经授权,禁止转载. 难度评级:☆☆☆☆官网地址:https://download.vulnhub.com/cengbox/CengB ...