『cs231n』线性分类器损失函数

代码部分

SVM损失函数 & SoftMax损失函数：

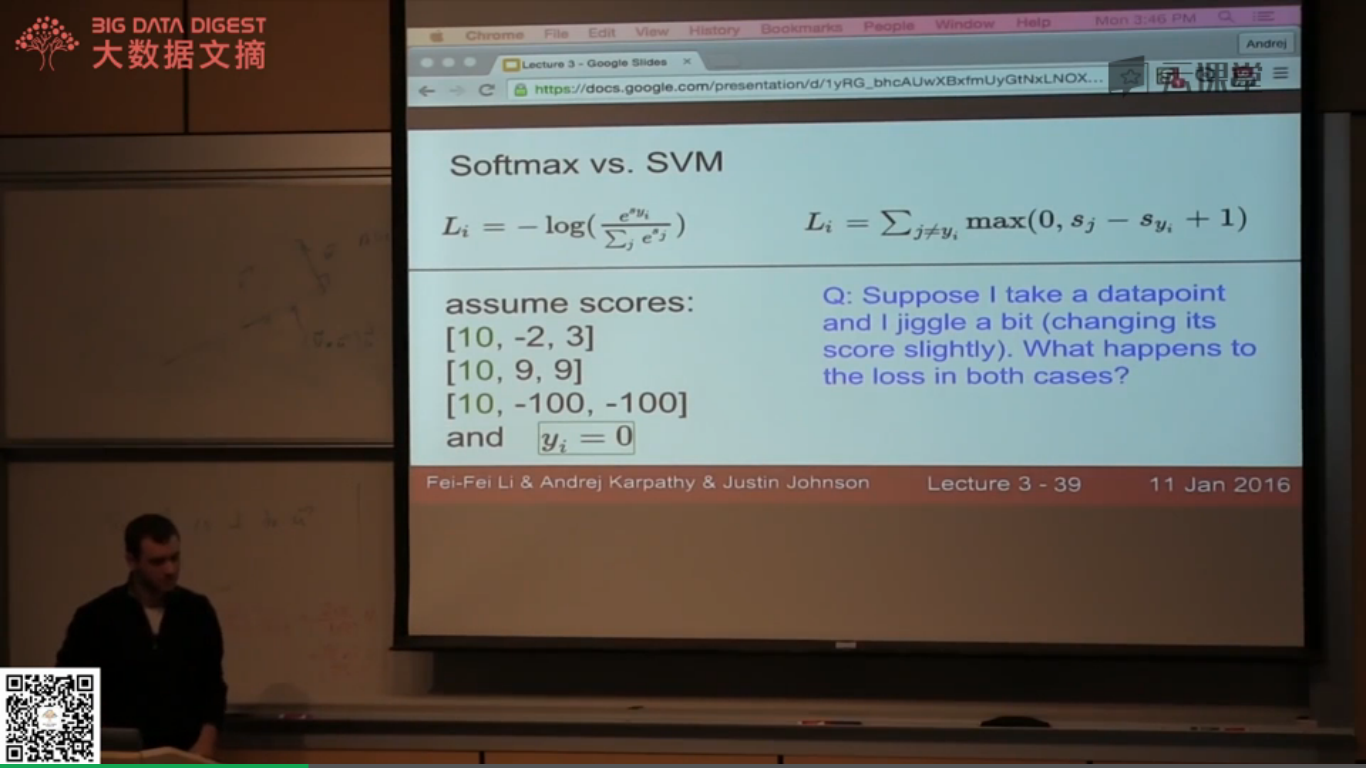
注意一下softmax损失的用法：

SVM损失函数：

import numpy as np

def L_i(x, y, W):
    '''
    非向量化SVM损失计算
    :param x: 输入矢量
    :param y: 标准分类
    :param W: 参数矩阵
    :return:
    '''
    delta = 1.0
    scores = W.dot(x)
    correct_score = scores[y]
    D = W.shap[0]
    loss_i = 0.0
    for j in range(D):
        if j==y:
            continue
        loss_i += max(0.0, scores[j] - correct_score + delta)
    return loss_i

def L_i_vectorized(x, y, W):
    '''
    半向量化SVM损失计算
    :param x: 输入矢量
    :param y: 标准分类
    :param W: 参数矩阵
    :return:
    '''
    delta = 1.0
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + delta)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

softmax分类器：

import numpy as np

# 正常的softmax分类器
f = np.array([123, 456, 789])
# p = np.exp(f) / np.sum(np.exp(f))
# print(p)

# 数值稳定化的softmax分类器
f -= np.max(f)
p = np.exp(f) / np.sum(np.exp(f))
print(p)

SoftMax实际应用

练习，softmax 模型：

Note: 你的 softmax(x) 函数应该返回一个形状和x相同的NumPy array类型。

例如，当输入为一个列表或者一维矩阵（用列向量表示一个样本样本）时，比如说以下的：

scores = [1.0, 2.0, 3.0]

应该返回一个同样长度（即3个元素）的一维矩阵：

print softmax(scores)
[ 0.09003057  0.24472847  0.66524096]

对于一个二维矩阵，如以下（列向量表示单个样本），例如:

scores = np.array([[1, 2, 3, 6],
                   [2, 4, 5, 6],
                   [3, 8, 7, 6]])

该函数应该返回一个同样大小(3,4)的二维矩阵，如以下:

[[ 0.09003057  0.00242826  0.01587624  0.33333333]
 [ 0.24472847  0.01794253  0.11731043  0.33333333]
 [ 0.66524096  0.97962921  0.86681333  0.33333333]]

每个样本（列向量）中的概率加起来应当等于 1。你可以用以上的例子来测试你的函数。

ANSWER:

"""Softmax."""

scores = [3.0, 1.0, 0.2]

import numpy as np

def softmax(x):
    """Compute softmax values for each sets of scores in x."""
    return np.exp(x)/np.sum(np.exp(x),axis=0)

print(softmax(scores))

# Plot softmax curves
import matplotlib.pyplot as plt
x = np.arange(-2.0, 6.0, 0.1)
scores = np.vstack([x, np.ones_like(x), 0.2 * np.ones_like(x)])
plt.plot(x, softmax(scores).T, linewidth=2)
plt.show()

比较好玩的是plt.plot(x, softmax(scores).T)中，后面的转置了，多线画图时，后面的都是要转置的，因为plt必须要求x和y第一维度大小相等：

plt.plot(np.linspace(0,1,100),np.asarray([10*np.linspace(0,2,100),10*np.linspace(0,1,100)]).T,linewidth=2)
# 可以绘图
# 查看一下shape：
np.linspace(0,1,100).shape
# Out[26]:
# (100,)
np.asarray([10*np.linspace(0,2,100),10*np.linspace(0,1,100)]).shape
# Out[25]:
# (2, 100)
# 必须对应x,y的第一维度大小

SoftMax特点

SoftMax（y*10）后分类器会更自信，SoftMax（y/10)后分类器会失去自信（结果概率平均化）

概念部分

损失函数=代价函数=目标函数

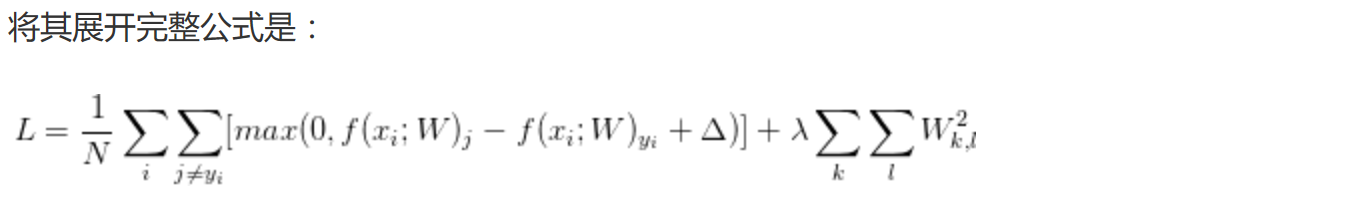
svm给出一个得分，softmax给出一个概率。