UVa 1595 Symmetry(set)

We call a figure made of points is left-right symmetric as it is possible to fold the sheet of paper along a vertical line and to cut the figure into two identical halves.For example, if a figure exists five points, which respectively are (-2,5),(0,0),(2,3),(4,0),(6,5). Then we can find a vertical line x = 2 to satisfy this condition. But in another figure which are (0,0),(2,0),(2,2),(4,2), we can not find a vertical line to make this figure left-right symmetric.

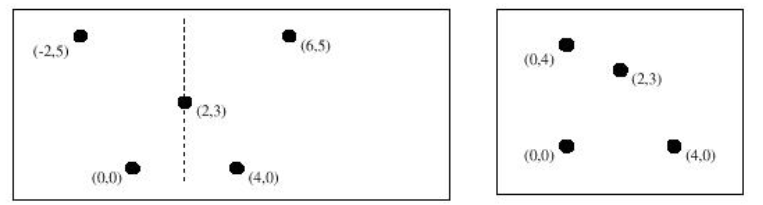
Write a program that determines whether a figure, drawn with dots, is left-right symmetric or not. The dots are all distinct.

Input
The input consists of T test cases. The number of test cases T is given in the first line of the input file. The first line of each test case contains an integer N, where N (1 <=N <= 1, 000) is the number of dots in a figure. Each of the following N lines contains the x-coordinate and y-coordinate of a dot. Both x-coordinates and y-coordinates are integers between −10, 000 and 10, 000, both inclusive.

Output
Print exactly one line for each test case. The line should contain 'YES' if the figure is left-right symmetric,and 'NO', otherwise.

Sample Input
3
5
-2 5
0 0
6 5
4 0
2 3
4
2 3
0 4
4 0
0 0
4
5 14
6 10
5 10
6 14

Sample Output
YES
NO
YES

题意

给你n个点，问是否可以找到一条竖线使得所有点对称

题解

首先去找竖线，竖线肯定在中间（注意竖线可以是小数），然后暴力所有点，查询对称点是否存在即可

代码

 #include<bits/stdc++.h>
 using namespace std;
 typedef pair<int,int> pi;
 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int T,n,a,b;
     cin>>T;
     while(T--)
     {
         set<pi> se;
         cin>>n;
         int left=1e9,right=-1e9,F=;
         for(int i=;i<n;i++)
         {
             cin>>a>>b;
             if(left>a)
                 left=a;
             if(right<a)
                 right=a;
             se.insert(pi(a,b));
         }
         double mid=(left+right)*0.5;
         pi ab;
         for(auto ab:se)
         {
             a=(int)*mid-ab.first;
             b=ab.second;
             if(!se.count(pi(a,b)))
             {
                 F=;
                 break;
             }
         }
         if(F)cout<<"YES"<<endl;
         else cout<<"NO"<<endl;
     }
     return ;
 }