「Luogu 1525」关押罪犯

Portal

Portal1: Luogu

Description

$S$城现有两座监狱，一共关押着$N$名罪犯，编号分别为$1 - N$。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为$c$ 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为$c$的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到S 城Z 市长那里。公务繁忙的Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了$N$名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使$\rm Z$市长看到的那个冲突事件的影响力最小？这个最小值是多少？

Input

每行中两个数之间用一个空格隔开。第一行为两个正整数$N, M$，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的$M$行每行为三个正整数$a_j, b_j, c_j$，表示$a_j$号和$b_j$号罪犯之间存在仇恨，其怨气值为$c_j$。数据保证$1<aj \le b_j \le N ,0 < cj \le 1, 000, 000, 000$，且每对罪犯组合只出现一次。

Output

共$1$ 行，为$\rm Z$市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出$0$。

Sample Input

Sample Output

Hint

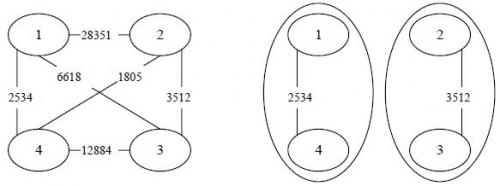
【输入输出样例说明】罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是$3512$（由$2$号和$3$号罪犯引发）。其他任何分法都不会比这个分法更优。

【数据范围】

对于$30\%$的数据有$N \le 15$。

对于$70\%$的数据有$N \le 2000,M \le 50000$。

对于$100\%$的数据有$N \le 20000,M \le 100000$。

Solution

题目要把罪犯们放到两个监狱，很容易想到是二分图。

我们可以先用二分答案，对于每一条大于二分出来的边（也就是不能放在一个监狱的两个罪犯，放入了答案就大于二分的值了）构成的图，判断是否能构成二分图，也就是是否可以将这些点分到两个区域。如果可以，那么说明了这个最大破坏度是可行的，所以就扩大二分值，最后求出最大值的最小值。

Code

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int MAXN = 100005, MAXM = 200005;
struct EDGE {
    int nxt, to, val;
} edge[MAXM];
int n, m, u, v, val, cnt, U[MAXN], V[MAXN], VAL[MAXN], col[MAXM], head[MAXM];
inline void addedge(int u, int v, int val) {//邻接表存图
    edge[++cnt].to = v; edge[cnt].val = val; edge[cnt].nxt = head[u]; head[u] = cnt;
}
inline bool check(int x) {//黑白染色，判断二分图
    queue<int> Q;
    memset(col, 0, sizeof(col));
    for (int i = 1; i <= n; i++)
        if (!col[i]) {
            Q.push(i);
            col[i] = 1;
            while (!Q.empty()) {
                int u = Q.front();
                Q.pop();
                for (int i = head[u]; ~i; i = edge[i].nxt) {
                    int v = edge[i].to;
                    if (edge[i].val >= x) {
                        if (!col[v]) {
                            col[v] = 3 - col[u];//标记状态（颜色）
                            Q.push(v);
                        } else
                        if (col[u] == col[v]) return 0;//如果冲突，就返回不是
                    }
                }
            }
        }
    return 1;
}
int main() {
    scanf("%d%d", &n, &m);
    int r = -1;
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= m; i++) {
        scanf("%d%d%d", &u, &v, &val);
        r = max(r, val);
        addedge(u, v, val);
        addedge(v, u, val);//双向边
    }
    r++;
    int l = 0;
    while (l + 1 < r) {//二分答案
        int mid = l + r >> 1;
        if (check(mid)) r = mid; else l = mid;
    }
    printf("%d\n", l);
    return 0;
}

Attachment

测试数据下载：https://www.lanzous.com/i7ayq3a