NOIP模拟赛 华容道 （搜索和最短路）蒟蒻的第一道紫题

题目描述

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面， 华容道是否根本就无法完成，如果能完成， 最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

1. 在一个 n \times mn×m 棋盘上有n \times mn×m个格子，其中有且只有一个格子是空白的，其余n \times m-1n×m−1个格子上每个格子上有一个棋子，每个棋子的大小都是 1 \times 11×1 的；

2. 有些棋子是固定的，有些棋子则是可以移动的；

3. 任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 qq 次，当然，每次棋盘上固定的格子是不会变的， 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 ii 次玩的时候， 空白的格子在第 EX_iEXi​ 行第 EY_iEYi​ 列，指定的可移动棋子的初始位置为第 SX_iSXi​ 行第 SY_iSYi​列，目标位置为第 TX_iTXi​ 行第 TY_iTYi​列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入格式

第一行有 33个整数，每两个整数之间用一个空格隔开，依次表示n,m,qn,m,q；

接下来的 nn 行描述一个n \times mn×m 的棋盘，每行有mm个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，00 表示该格子上的棋子是固定的，11 表示该格子上的棋子可以移动或者该格子是空白的。

接下来的 qq 行，每行包含 66 个整数依次是 EX_i,EY_i,SX_i,SY_i,TX_i,TY_iEXi​,EYi​,SXi​,SYi​,TXi​,TYi​，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式

共qq 行，每行包含 11 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1−1。

输入输出样例

输入 #1复制

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

输出 #1复制

2
-1

说明/提示

【输入输出样例说明】

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

1. 第一次游戏，空白格子的初始位置是 (3,2)(3,2)（图中空白所示），游戏的目标是将初始位置在(1, 2)(1,2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)(2,2)（图中红色的格子）上。

移动过程如下：

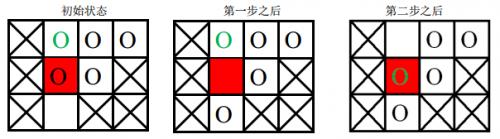
1. 第二次游戏，空白格子的初始位置是(1, 2)(1,2)（图中空白所示），游戏的目标是将初始位置在(2, 2)(2,2)上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)(3,2)上。

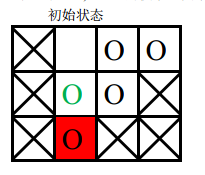
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置(2,2)(2,2)上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置， 游戏无法完成。

【数据范围】

对于30\%30%的数据，1 ≤ n, m ≤ 10,q = 11≤n,m≤10,q=1；

对于 60\%60%的数据，1 ≤ n, m ≤ 30,q ≤ 101≤n,m≤30,q≤10；

对于 100\%100%的数据，1 ≤ n, m ≤ 30,q ≤ 5001≤n,m≤30,q≤500。

思路（题解）

• 这题zwjdd大佬看到的第一反应就是打个暴力，胖哥来了句A星，感觉大佬们都是神仙。
• 这题看一下数据范围，有了第一反应，把空格移动，打个bfs，感觉就有分了。然后感觉这是考试的最后题，这么搞应该不对吧，然后手玩了一下感觉会T，预计没有几分。

讲一下正解：

• 其实主思路还是一样的，但我们可以去优化！！！，只要优化，感觉正常的题目都可以。
• 就是一个贪心的想法，为了成功，一定要先把空格移动到指定格的旁边，这样，指定格才有可能移动到空格上，其次，当空格已经到了棋子之后就尽量不要再改，要改除非是要让开一个位置，或者其他什么特别的操作，但最后还是都会回到旁边。
• 这时我们会发现，原来是一次移动一次空格，现在是将空格从指定格的某一个方向变成另一个方向，就像这样。
• 
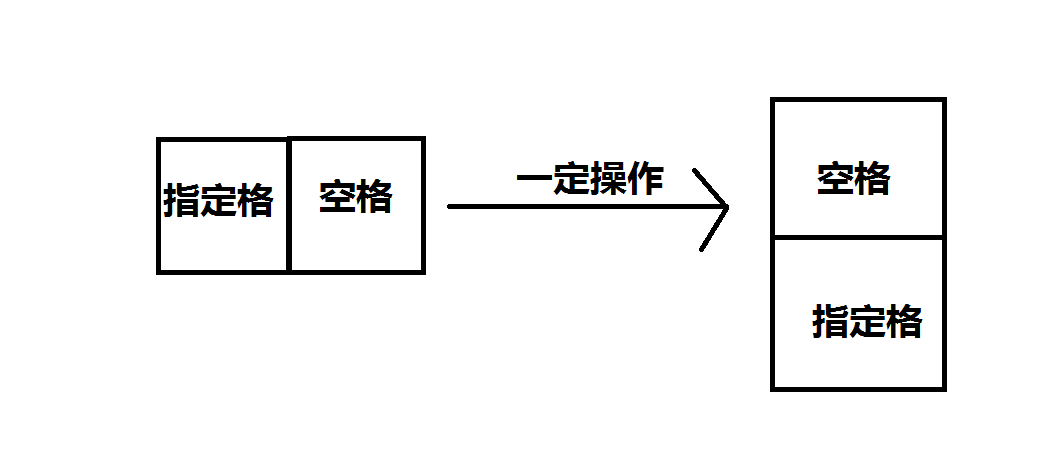
• 所以我们可以把这个东西给预处理出来，我们开一个4维数组，skep[ i ] [ j ] [ f1 ] [ f2 ],表示在格子是（i，j）时，将空格从他的f1方向，改到f2方向，并与指定格交换 时的步数，其实就是交换前的步数+1.
• 为了方便，我们这样

1. 1表示在上面。
2. 2表示在下面。
3. 3表示在左边。
4. 4表示在右边。

• 其实求法很简单，不需要搞什么高大上的方法，就直接搞四个循环去枚举skep的参数，从f1 上开始bfs
• 注意：很重要，不然会错很多次，在bfs时，要把指定格标记为不可走，不然指定格如果动了，那就有趣多了。
• 在bfs之后再把标记给改回来，最后把空格和指定格交换一下就可以了。
• 此时，这道题目就很像一个有用的算法了-----图论。
• 图中的点就是（i，j，k），f表示方向，（i，j）表示在原矩阵的第i行，第j列，每一个skep[i][j][f1][f2]就是一条边，表示从（i，j，f1）到（i，j，f3），f3 表示f2的相对方向。

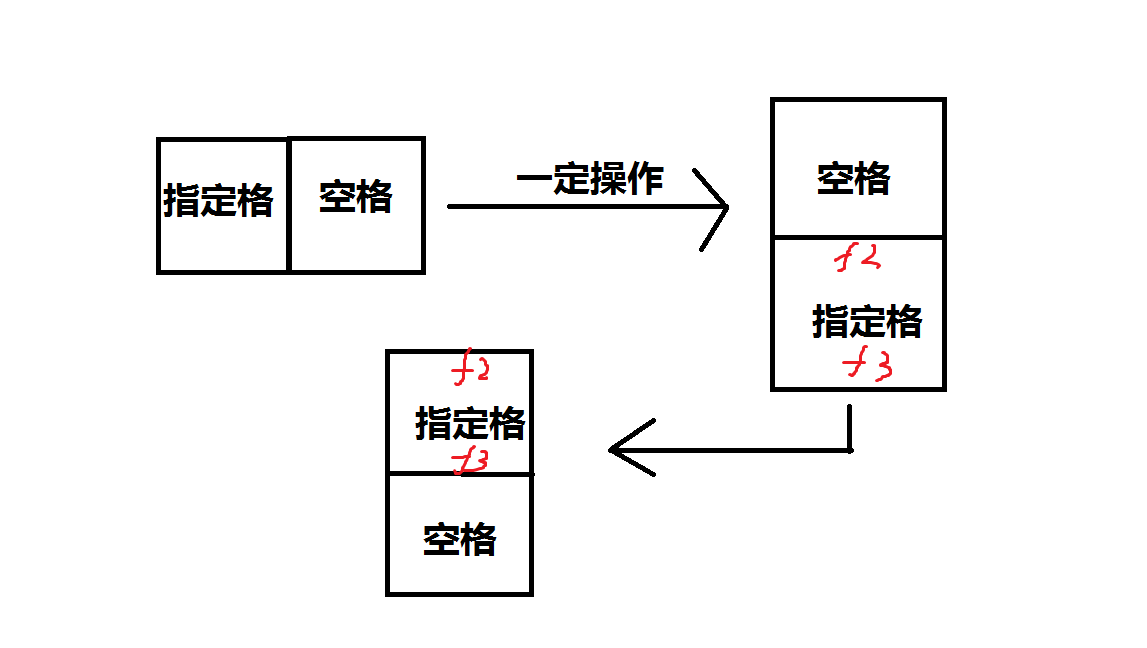
• 然后在图上跑一跑最短路就可以了，因为没卡，所以就写了SPFA（其实是好写，太懒了）

总结一下打题时的打题过程：

1. 预处理出来所有的skep;
2. 把空格移到指定格的周围。
3. 一顿瞎搞之后，开始最短路。
4. 还有就是如果本该就在目标位置上，就可以直接输出0；

代码：

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 using namespace std;
 const int maxn = ;
 const int maxf = ;
 const int inf = ;
 const int ff[] = {, , , , }; //这个是i的相反方向
 struct pos                         //位置
 {
     int x, y;
     pos()
     {
         return;
     }
     pos(int a, int b)
     {
         x = a;
         y = b;
     }
 };
 struct queue_data
 {
     int x, y, f;
 };

 int n, m;
 int Mat[maxn][maxn];
 pos f[maxf];
 int Skip[maxn][maxn][maxf][maxf];
 int Dist[maxn][maxn][maxf]; //最短路里的距离
 bool vis[maxn][maxn][maxf];
 queue<queue_data> q;
 pos operator+(pos A, pos B) //为了向四周移动，把加法重载了一下
 {
     return (pos){A.x + B.x, A.y + B.y};
 }
 queue_data operator+(queue_data A, pos B)
 {
     return (queue_data){A.x + B.x, A.y + B.y, A.f};
 }
 int Bfs(pos st, pos ed) //求从开始点到目的点的步数
 {
     if ((Mat[st.x][st.y] == ) || (Mat[ed.x][ed.y] == )) //当这两个点中有任意一个不可走时，直接返回无穷大
     {
         return inf;
     }
     //各种初始化
     queue<pos> q;
     while (!q.empty())
     {
         q.pop();
     }
     bool vis[maxn][maxn];
     int Dist[maxn][maxn];
     memset(vis, , sizeof(vis));
     memset(Dist, , sizeof(Dist));
     //将st放入队列
     q.push(st);
     vis[st.x][st.y] = ;
     Dist[st.x][st.y] = ;
     do
     {
         pos u = q.front();
         q.pop();
         for (int i = ; i <= ; i++) //枚举向四个方向走
         {
             pos v = u + f[i];
             if ((Mat[v.x][v.y] == ) || (vis[v.x][v.y] == ))
             {
                 continue;
             }
             vis[v.x][v.y] = ;
             Dist[v.x][v.y] = Dist[u.x][u.y] + ;
             q.push(v);
         }
     } while (!q.empty()); //返回步数
     return Dist[ed.x][ed.y];
 }
 void pre()
 {
     f[] = (pos){-, };
     f[] = (pos){, }; //枚举向那个方向移动时使用
     f[] = (pos){, -};
     f[] = (pos){, };
     memset(Skip, , sizeof(Skip));
     for (int i = ; i <= n; i++) //四重循环枚举(i,j)，空格所在方向f1，要将(i,j)移动去的方向f2
     {
         for (int j = ; j <= m; j++)
         {
             if (Mat[i][j] == ) //若(i,j)本身不可走则不进行操作
             {
                 continue;
             }
             Mat[i][j] = ; //因为不能在移动空格的时候使(i,j)被移动，所以先置为不能走
             pos now(i, j);
             for (int f1 = ; f1 <= ; f1++) //枚举方向
             {
                 for (int f2 = ; f2 <= ; f2++)
                 {
                     if (f1 > f2) //空格在f1，当前格走到f2和空格在f2，当前格走到f1的步数是一样的
                     {
                         Skip[i][j][f1][f2] = Skip[i][j][f2][f1];
                         continue;
                     }
                     Skip[i][j][f1][f2] = Bfs(now + f[f1], now + f[f2]) + ;
                 }
             }
             Mat[i][j] = ; //置回来
         }
     }
     return;
 }

 int main()
 {
     int qus; //询问个数
     cin >> n >> m >> qus;
     for (int i = ; i <= n; i++)
     {
         for (int j = ; j <= m; j++)
         {
             cin >> Mat[i][j];
         }
     }
     pre(); //将skep预处理一下
     while (qus--)
     {
         int epx, epy, stx, sty, glx, gly;
         cin >> epx >> epy >> stx >> sty >> glx >> gly;
         if ((Mat[stx][sty] == ) || (Mat[glx][gly] == ))
         {
             cout << "-1" << endl; //初始位置和目的位置都不通时
             continue;
         }
         if ((stx == glx) && (sty == gly))
         {
             cout << "" << endl; //自己就在终点上时
             continue;
         }

         while (!q.empty()) //初始化一下，机房大佬出版的《模拟赛的几百个错误》中经常出现的东西
             q.pop();
         memset(Dist, , sizeof(Dist));
         memset(vis, , sizeof(vis));
         Mat[stx][sty] = ;
         //求出将空白格移动到指定格初始位置四周的步数，并将其中可行的放入队列
         //因为要求出空白格移动的步数，所以这时初始位置不能动，先置为0表示不可走
         pos init = (pos){stx, sty};
         for (int i = ; i <= ; i++)
         {
             pos v = init + f[i];                         //枚举周围的点
             Dist[stx][sty][i] = Bfs((pos){epx, epy}, v); //用bfs求出步数
             if (Dist[stx][sty][i] != inf)
             {
                 q.push((queue_data){stx, sty, i}); //如果可以，就放到队列里
             }
         }
         Mat[stx][sty] = ; //在跑完之后把指定点还原
         while (!q.empty()) //最短路
         {
             queue_data u = q.front();
             q.pop();
             vis[u.x][u.y][u.f] = ;
             for (int i = ; i <= ; i++) //枚举4个方向
             {
                 queue_data v = u + f[i];
                 v.f = ff[i]; //这里空格的方向要改成反方向
                 if (Dist[v.x][v.y][v.f] > Dist[u.x][u.y][u.f] + Skip[u.x][u.y][u.f][i])
                 {
                     Dist[v.x][v.y][v.f] = Dist[u.x][u.y][u.f] + Skip[u.x][u.y][u.f][i];
                     if (vis[v.x][v.y][v.f] == )
                     {
                         q.push(v);
                         vis[v.x][v.y][v.f] = ;
                     }
                 }
             }
         }
         int ans = inf;
         for (int i = ; i <= ; i++)
         {
             ans = min(ans, Dist[glx][gly][i]); //找出最小值
         }
         if (ans == inf)
         {
             ans = -;
         }
         cout << ans << endl;
     }
     return ;
 }