HDU 4444：Walk（思维建图+BFS）***

http://acm.hdu.edu.cn/showproblem.php?pid=4444

题意：给出一个起点一个终点，给出n个矩形的两个对立顶点，问最少需要拐多少次弯可以从起点到达终点，如果不能输出-1.

思路：http://blog.csdn.net/asdfgh0308/article/details/8125832看的是这里的。

因为边界是可以走的，所以不能用点直接来做。

这里用到的就是把一个点拆成一个3*3的方块，中心点就是本身，然后对图进行染色。举个染色的例子：

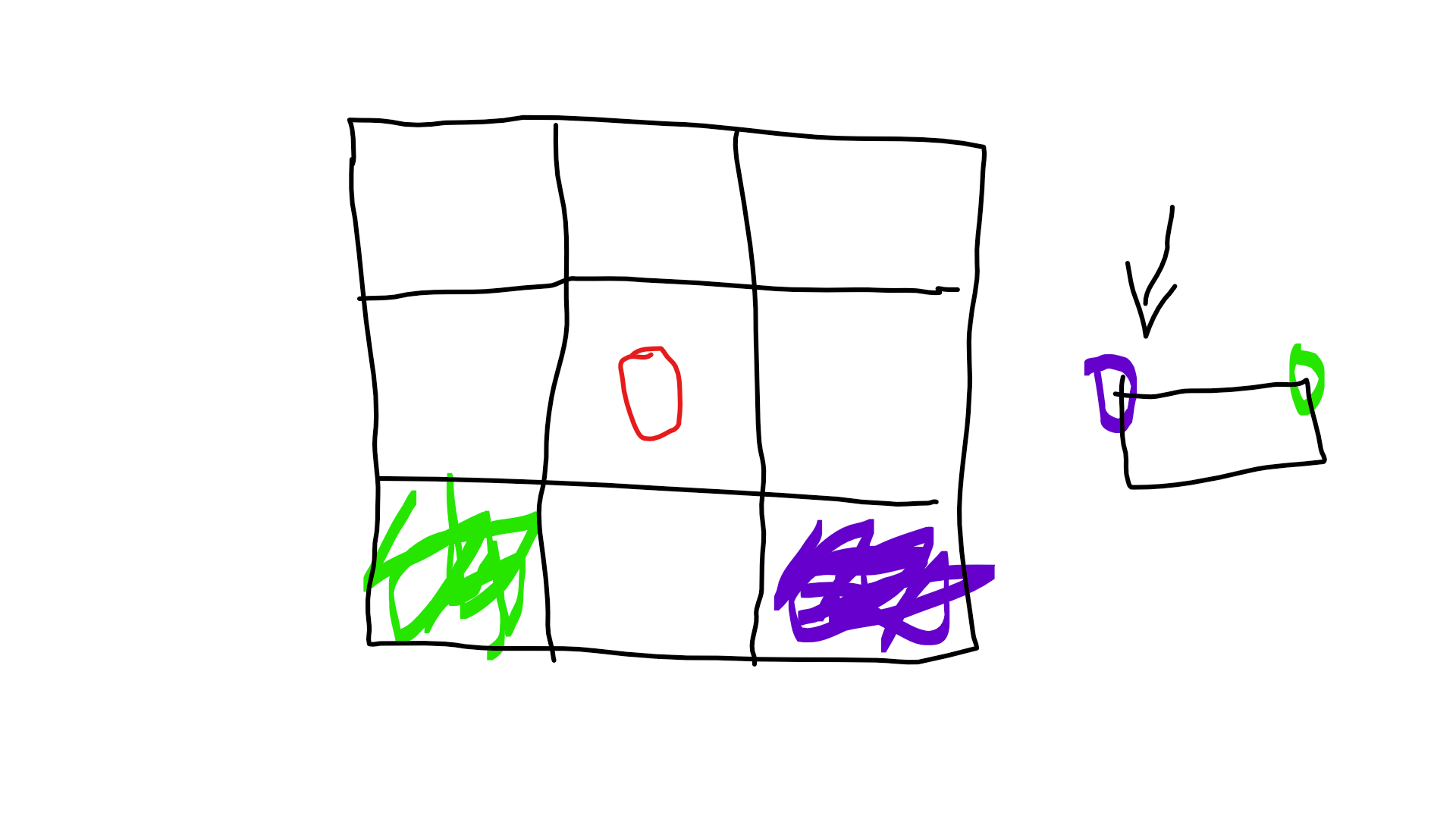
如果染的是某个颜色的顶点，那么对于那个顶点应当将3*3的方块那样染。

接下来就考虑一种‘L’型拐角的怎么去拐，很多种情况需要去列举。

还有一种就是点的两侧都是被染过的，说明这是一个有两条边界相交的点，因此也是不能走的。

还有注意循环结束的条件不是(SX +SY + EX + EY)，因为点可以是负，因这个WA了一个晚上才发现！！！

 #include <bits/stdc++.h>
 using namespace std;
 #define N 1010
 #define INF 0x3f3f3f3f
 struct node {
     int x, y;
 } p[N][];
 struct P {
     int x, y, dir;
     P () {}
     P (int _x, int _y, int _dir) : x(_x), y(_y), dir(_dir) {};
 };
 int xx[N], yy[N], x[N], y[N], cx, cy, n, sx, sy, ex, ey;
 int mp[N][N], dis[N][N][], dx[] = {, -, , }, dy[] = {, , , -}; // 上下右左
 bool vis[N][N][];
 void Addpoint(int &x, int &y) {
     x *= , y *= ;
     cx++; xx[cx] = x;
     cx++; xx[cx] = x + ;
     cx++; xx[cx] = x - ;
     cy++; yy[cy] = y;
     cy++; yy[cy] = y + ;
     cy++; yy[cy] = y - ;
 }
 void Find(int &wx, int &wy) {
     wx = lower_bound(xx + , xx +  + cx, wx) - xx;
     wy = lower_bound(yy + , yy +  + cy, wy) - yy;
 }
 void Turn(int x, int y) {
     if(mp[x-][y-] && mp[x+][y+] && mp[x+][y-] && mp[x-][y+]) mp[x][y] = -; // 四个角都不行
     else if(mp[x+][y+] && mp[x+][y-] && mp[x-][y+]) mp[x][y] = ; // 左下角可以
     else if(mp[x+][y-] && mp[x+][y+] && mp[x-][y-]) mp[x][y] = ; // 右下角可以
     else if(mp[x-][y-] && mp[x-][y+] && mp[x+][y-]) mp[x][y] = ; // 右上角可以
     else if(mp[x-][y-] && mp[x-][y+] && mp[x+][y+]) mp[x][y] = ; // 左上角可以
     else if(mp[x+][y-] && mp[x-][y+]) mp[x][y] = ; // 左下角右上角可以
     else if(mp[x-][y-] && mp[x+][y+]) mp[x][y] = ; // 左上角右下角可以
     if(mp[x-][y] && mp[x+][y]) mp[x][y] = -;
     if(mp[x][y-] && mp[x][y+]) mp[x][y] = -;
 }
 void Build() {
     memset(mp, , sizeof(mp));
     for(int i = ; i <= n; i++)
         for(int j = p[i][].x + ; j <= p[i][].x - ; j++)
             for(int k = p[i][].y + ; k <= p[i][].y - ; k++)
                 mp[j][k] = -;
     for(int i = ; i <= cx; i++)
         for(int j = ; j <= cy; j++)
             if(!mp[i][j]) Turn(i, j);
 }
 bool Check(int x, int y, int nx, int ny, int pdir, int dir) {
     if(nx <  || nx > cx || ny <  || ny > cy) return false;
     if(!mp[x][y]) return true;
     if(dir == ) { // 上
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
     } else if(dir == ) { // 下
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
     } else if(dir == ) {
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
     } else {
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
         if(pdir ==  && (mp[x][y] ==  || mp[x][y] == )) return true;
     }
     return false;
 }

 int BFS() {
     memset(vis, , sizeof(vis));
     memset(dis, INF, sizeof(dis));
     queue<P> que; while(!que.empty()) que.pop();
     for(int i = ; i < ; i++) {
         que.push(P(sx, sy, i)), dis[sx][sy][i] = , vis[sx][sy][i] = ;
     }
     int ans = INF;
     while(!que.empty()) {
         P now = que.front(); que.pop();
         int x = now.x, y = now.y, dir = now.dir;
         if(x == ex && y == ey) ans = min(ans, dis[x][y][dir]);
         vis[x][y][dir] = ;
         for(int k = ; k < ; k++) {
             int nx = now.x + dx[k], ny = now.y + dy[k], ndir = k;
             if(!Check(x, y, nx, ny, dir, ndir)) continue;
             int w = ndir == dir ?  : ; w += dis[x][y][dir];
             if(w < dis[nx][ny][ndir]) {
                 dis[nx][ny][ndir] = w;
                 if(!vis[nx][ny][ndir]) vis[nx][ny][ndir] = , que.push(P(nx, ny, ndir));
             }
         }
     }
     if(ans == INF) puts("-1");
     else printf("%d\n", ans);
 //    puts("");
 }
 int main() {
     while(scanf("%d%d%d%d", &sx, &sy, &ex, &ey)) { // sx + sy + ex + ey == 0
         if(!sx && !sy && !ex && !ey) break;
         scanf("%d", &n); cx = cy = ;
         for(int i = ; i <= n; i++) {
             int x1, x2, y1, y2;
             scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
             Addpoint(x1, y1); Addpoint(x2, y2);
             if(x1 > x2) swap(x1, x2);
             if(y1 > y2) swap(y1, y2);
             p[i][] = (node) { x1, y1 };
             p[i][] = (node) { x2, y1 };
             p[i][] = (node) { x2, y2 };
             p[i][] = (node) { x1, y2 };
         }
         Addpoint(sx, sy); Addpoint(ex, ey);
         int tx = cx, ty = cy;
         sort(xx + , xx +  + cx); cx = unique(xx + , xx +  + cx) - xx - ;
         sort(yy + , yy +  + cy); cy = unique(yy + , yy +  + cy) - yy - ;
         for(int i = ; i <= n; i++)
             for(int j = ; j < ; j++)
                 Find(p[i][j].x, p[i][j].y);
         Find(sx, sy); Find(ex, ey);
         Build();
         BFS();
     }
     return ;
 }