通俗地说逻辑回归【Logistic regression】算法（一）

在说逻辑回归前，还是得提一提他的兄弟，线性回归。在某些地方，逻辑回归算法和线性回归算法是类似的。但它和线性回归最大的不同在于，逻辑回归是作用是分类的。

还记得之前说的吗，线性回归其实就是求出一条拟合空间中所有点的线。逻辑回归的本质其实也和线性回归一样，但它加了一个步骤，逻辑回归使用sigmoid函数转换线性回归的输出以返回概率值，然后可以将概率值映射到两个或更多个离散类。

如果给出学生的成绩，比较线性回归和逻辑回归的不同如下：

• 线性回归可以帮助我们以0-100的等级预测学生的测试分数。线性回归预测是连续的（某个范围内的数字）。
• Logistic回归可以帮助预测学生是否通过。逻辑回归预测是离散的（仅允许特定值或类别）。我们还可以查看模型分类背后的概率值。

一.从回归到分类的核心 --Sigmoid Function

之前介绍线性回归的时候，它的函数是这样样子的：

h(x)=θ0 + θ1 * x1 + θ2 * x2 + θ3 * x3 ...

但这样的函数是没办法进行分类的工作的，所以我们要借助一下其他函数，那就是Sigmoid Function。

我们先来看看这个Sigmoid Function长什么样，Sigmoid Function的数学公式是这样子的：

如果表示在平面坐标轴上呢，那它长这个样子。

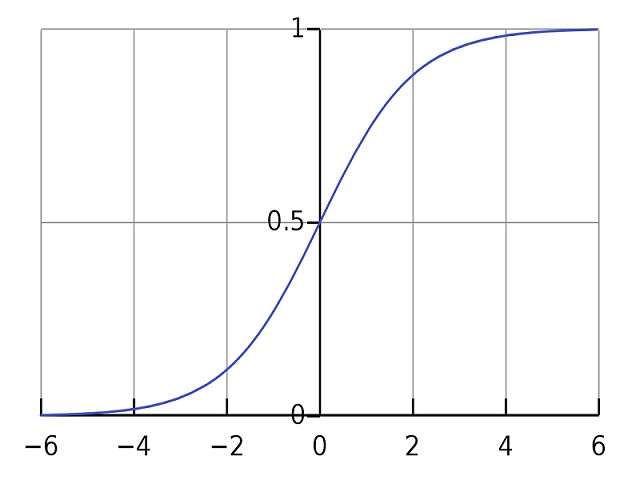
这个Sigmoid Function可以将线性的值，映射到[0-1]这个范围中。如果映射结果小于0.5，则认为是负的样本，如果是大于0.5，则认为是正的样本。

比方说要对垃圾邮箱进行分类，分垃圾邮箱和正常邮箱。当这个Sigmoid Function的计算出来后，小于0.5，则认为是垃圾邮箱，大于0.5则是非垃圾邮箱。

原先线性回归的计算公式是这样的：

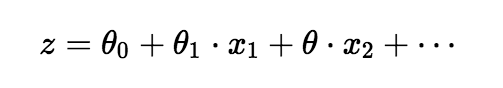
那么将这个z函数代入到Sigmoid Function中，OK，现在我们就有了一个逻辑回归的函数了。

二.代价函数Cost Function

和线性回归一样，逻辑回归也有代价函数。并且都是通过最小化Cost Function来求得最终解的。

我们先来看单个点的情况，

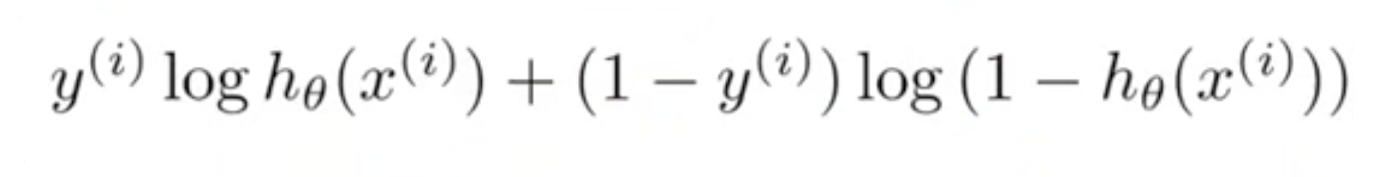
这个代价函数呢，叫做交叉熵，其中y(i)指的是预测的结果，而hθ(xi)指的是xi这个点原本的值。

那么它具体是什么意思呢，为什么叫做交叉熵？我们举两个极端的例子看看就明白了：

1.xi原始值hθ=1，预测结果，yi=1的情况

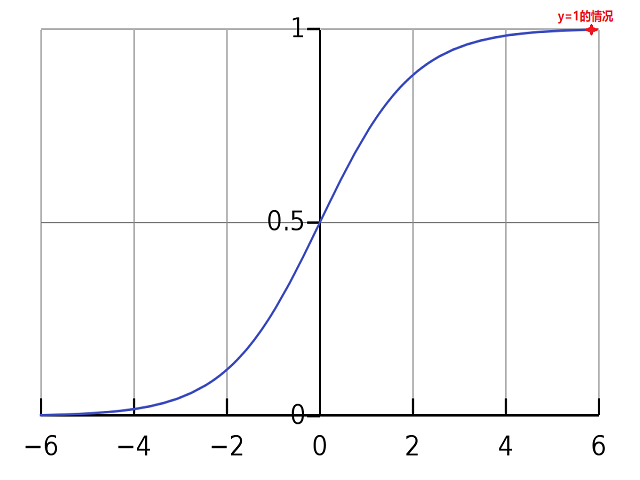
这个时候，代价函数的加号右边会被消掉，因为右边（1-y(i)）是0，左边部分呢，因为hθ(xi)=1，故而log(1)=0。

y(i)log(hθ(xi)) = 1 * log(0) = 0

也就是说，若xi原始值是1，当预测值y=1的时候，代价函数是0的。这个也比较好理解，代价函数为0就是说预测结果和原始结果完全一致的，没有半点出差错。

2.计算结果，yi=0，原始值hθ=0

这次的结果就和上面的反过来了，因为yi=0，所以左边部分全军覆没，来看右边，

(1-yi) * log(1-hθ(xi)) = 1 * log(0) = 0

因为1-hθ(xi)，最终结果还是等于0。

也就是说，这个损失函数，只要原始值与预测结果越相符，损失函数就越大，反之，损失函数就会越小。

以上说的只是一个点的情况，实际的代价函数，是要计算所有点的损失函数的均值，如下所示：

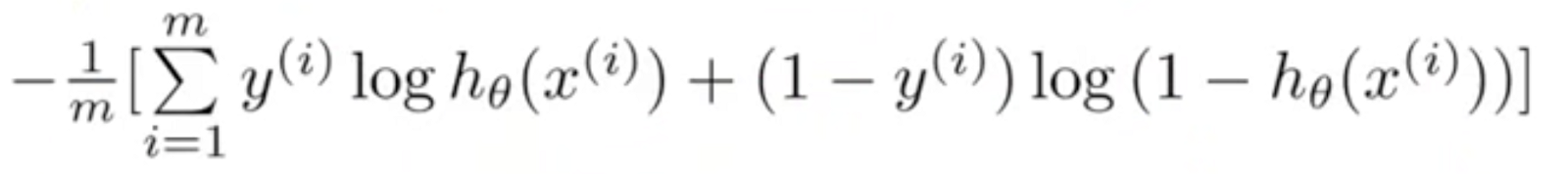
三.梯度下降

和线性回归一样，逻辑回归的解法也可以通过梯度下降来进行求解。梯度下降的目的，是为了最小化代价函数Cost function。

要求使用梯度下降，需要先求解偏导数，以下是求导数的一个具体过程：

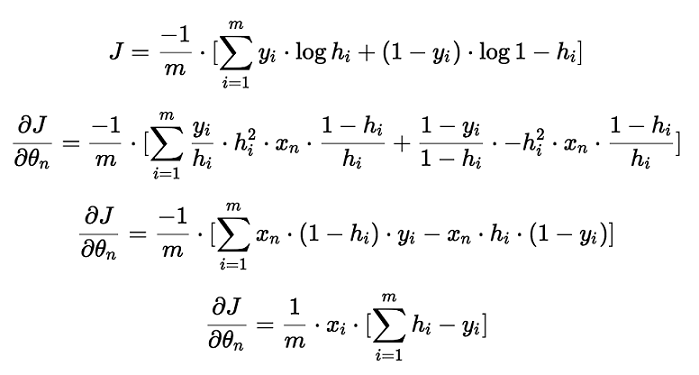
而梯度下降的计算方法也和线性回归的计算方法是一样的。只是其中的代价函数，换成了逻辑回归的代价函数。

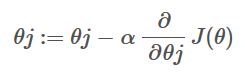
其中，α右边部分对应我们上面对代价函数求偏导的结果。而α是用来控制训练速率的，这个在线性回归那里已经有说到，这里就不再介绍了。

最终就是对θj不断迭代，直到损失函数降到最小，那就可以求出我们要的θ值了。

四.小结

OK，今天介绍了线性回归和逻辑回归的区别，同样都是回归分析，逻辑回归能完成分类任何的核心，就算使用了Sigmoid Function。

这里留一个小问题，上面所述的逻辑回归，通常是仅仅能够进行二分类，那有没有办法来让逻辑回归实现多分类呢？

下一次将阐述用逻辑回归进行多分类，以及正则化相关内容，并介绍sklearn的逻辑回归参数和用法！！

以上~~

---

推荐阅读：
通俗得说线性回归算法（一）线性回归初步介绍
通俗得说线性回归算法（二）线性回归初步介绍
Scala 函数式编程指南（一） 函数式思想介绍
通俗地说决策树算法（二）实例解析
大数据存储的进化史 --从 RAID 到 Hadoop Hdfs
C，java，Python，这些名字背后的江湖！