[P2216] [HAOI2007]理想的正方形 「单调队列」

思路：用单调队列分别维护行与列。

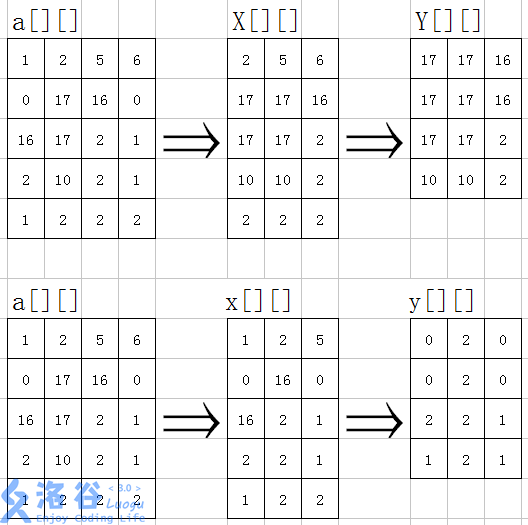
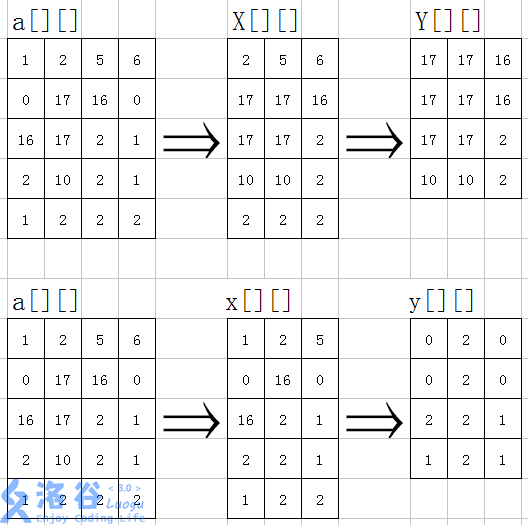
具体实现方法：是先用单调队列对每一行的值维护，并将a[][]每个区间的最大值，最小值分别存在X[][]和x[][]中。

那么X[][]与x[][]所存储的分别是1×n的长方形内的最大值，最小值。X[i][j]存储第i行第j~j+n-1列的长方形中的最大值。同理，x[i][j]存储第i行第j~j+n-1列的长方形中的最小值。

这时再对这两个数组的每一列上的值进行维护，将X[][]中每个区间的的最大值用Y[ ][ ]维护，将x[][]中的每个区间的最小值用y[][]维护。那么Y[i][j]存储X[][]中第i~i+n-1行第j列的长方形的最大值。同理y[i][j]存储x[][]中第i~i+n-1行第j列的长方形的最小值。

故Y[i][j]存储的实为以a[i~i+n-1][j~j+n-1]中的最大，即以i，j为左上角，边长为n的正方形中的最大值。同理，y[i][j]存储的即以i，j为左上角，边长为n的正方形中的最小值。

模拟过程见下图：

 Code

#include <bits/stdc++.h>
using namespace std;

int n,m,k,front,FRONT,back,BACK,ans;
int a[][],q[],Q[];
int x[][],X[][];
int y[][],Y[][];

int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for (int I=;I<=n;I++)
        for (int i=;i<=m;i++)
            scanf("%d",&a[I][i]);
    for (int I=;I<=n;I++)
        {
            FRONT=BACK=front=back=Q[]=q[]=;
            for (int i=;i<=m;i++)
                {
                    while (a[I][i]>=a[I][Q[BACK]]&&FRONT<=BACK) BACK--;
                    while (a[I][i]<=a[I][q[back]]&&front<=back) back--;
                    BACK++;back++;Q[BACK]=i;q[back]=i;
                    while (i-Q[FRONT]>=k) FRONT++;
                    while (i-q[front]>=k) front++;
                    if (i>=k) X[I][i-k+]=a[I][Q[FRONT]],x[I][i-k+]=a[I][q[front]];
                }
        }
    for (int I=;I<=m-k+;I++)
        {
            FRONT=BACK=front=back=Q[]=q[]=;
            for (int i=;i<=n;i++)
                {
                    while (X[i][I]>=X[Q[BACK]][I]&&FRONT<=BACK) BACK--;
                    while (x[i][I]<=x[q[back]][I]&&front<=back) back--;
                    BACK++;back++;Q[BACK]=i;q[back]=i;
                    while (i-Q[FRONT]>=k) FRONT++;
                    while (i-q[front]>=k) front++;
                    if (i>=k) Y[i-k+][I]=X[Q[FRONT]][I],y[i-k+][I]=x[q[front]][I];
                }
        }
    ans=0x3f3f3f3f;
    for (int I=;I<=n-k+;I++)
        for (int i=;i<=m-k+;i++)
            ans=min(ans,Y[I][i]-y[I][i]);
    printf("%d\n",ans);
    return ;
}