四、排序算法总结二（归并排序）（C++版本）

一、什么是归并排序？

　　归并排序是基于分而治之的思想建立起来的。

　　所谓的分而治之，也就是将一个数据规模为N的数据集，分解为两个规模大小差不多的数据集（n/2）,然而分别处理这两个更小的问题，就相当于解决了总的问题。

二、归并排序的思路。

　　1-首先将数据分为左右相等的两部分，不断细分，到最后只有单个元素。

　　2-再将相邻的两个元素集合（只是规模为1）排序，变为 n/2 个规模为2的数据序列。

　　随后不断的合并数据集并且排序，直到最后得到了一个完整的数据有序序列。

三、一个简单的例子。

　　下图是一个数据规模为8的数据集的排序过程。

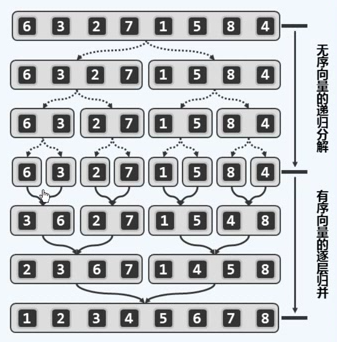
　　最开始8个数据不断地细分，知道不可再分（数据数目为一）

　　随后开始进行排序，将相邻的两个数据集排序合并，形成3 6，2 7,  1 5 ，4, 8

　　随后不断地向上排序，知道合并成一个完整的有序数据序列。

四 算法功能

　　上面的过程说明了算法需要完成的两个的算法功能

　　一是对于数据二分的过程，直到不可再分

　　二是对于两个数据集排序合并，形成一个更大的数据集的过程。

五、算法实现

　　1-递归版本

 #include <stdlib.h>
 #include <stdio.h>

 void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex)
 {
     int i = startIndex, j=midIndex+, k = startIndex;
     while(i!=midIndex+ && j!=endIndex+)
     {
         if(sourceArr[i] > sourceArr[j])
             tempArr[k++] = sourceArr[j++];
         else
             tempArr[k++] = sourceArr[i++];
     }
     while(i != midIndex+)
         tempArr[k++] = sourceArr[i++];
     while(j != endIndex+)
         tempArr[k++] = sourceArr[j++];
     for(i=startIndex; i<=endIndex; i++)//这里的复制是从头到尾的，
                                                          //我之前就是这里出了问题
         sourceArr[i] = tempArr[i];
 }

 //内部使用递归
 void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
 {
     int midIndex;
     if(startIndex < endIndex)
     {
         midIndex = startIndex + (endIndex-startIndex) / ;//避免溢出int
         MergeSort(sourceArr, tempArr, startIndex, midIndex);
         MergeSort(sourceArr, tempArr, midIndex+, endIndex);
         Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
     }
 }

 int main(int argc, char * argv[])
 {
     int a[] = {, , , , , , , };
     int i, b[];
     MergeSort(a, b, , );
     for(i=; i<; i++)
         printf("%d ", a[i]);
     printf("\n");
     return ;
 }

2-迭代版本

　　（待补充）

六、复杂度

　　时间复杂度:  O(n log n)

　　空间复杂度：O(n)