【前端】 在前端利用数学函数知识+box-shadow解波浪图形
序
今天正在刷数学函数相关题目，刷到了下面这篇文章，哇哦～有意思。 利用cos和sin实现复杂的曲线。传送门在下面。
CSS 技巧一则 -- 在 CSS 中使用三角函数绘制曲线图形及展示动画
正巧在复习一些数学知识，遂动手实践了一把使用 数学中的函数 使用css画连续曲线。
函数: 第一步
在数学中 函数 是指 ，一组定义域通过一组表达式， 映射到一组值域，也就是说 函数 f(x) = x^2 表示一个集合，每个输入x，固定通过x^2返回一个值y，由此定义可得：
当集合 X = {-2, -1, 0, 1, 2} 输入到函数f，得到的值域集合 Y = { y | y >= 0 }。
我们也可以通过列表格，更直观的列举出函数的值：
当x = 1 时 y等于 1
当x = 2时 y等于 4
| x= | -2 | -1 | 0 | 1 | 2 | ... |
| y= | 4 | 1 | 0 | 1 | 4 | ... |
由这个表格，我们可以在坐标轴画出关于y = f(x) = x^2的函数的样子：
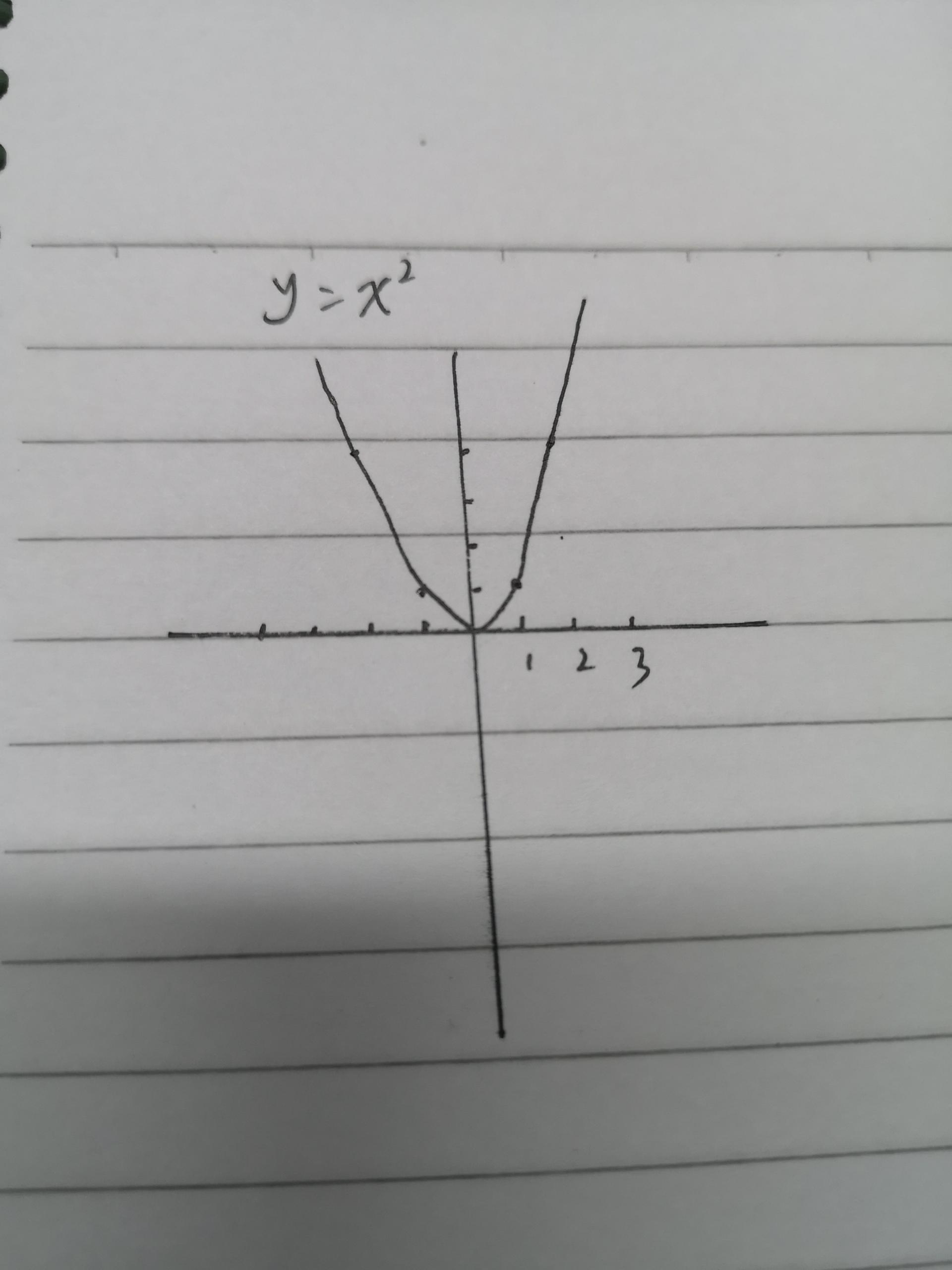
开口控制
如果我们在y = x^2 加个负号会怎么样呢,y = f(x) = -(x ^ 2)
图像会倒过来变成像 n 这样的样子？
就这样，我们可以通过这个函数，得到两种曲线，正的u 和 反的n。 那么问题来了，要画任意曲线，那么意味着，曲线要可大可小，可以在图中的任意一个位置，要怎么办呢？
嗯 仔细想想，如果函数 f(x) = x^2 再让它除以-2呢
f(x) = x^2 / -2
| x= | -2 | -1 | 0 | 1 | 2 | ... |
| y= | -2 | -1/2 | 0 | -1 /2 | -2 | ... |
手动画一下图像大约长下面这样：
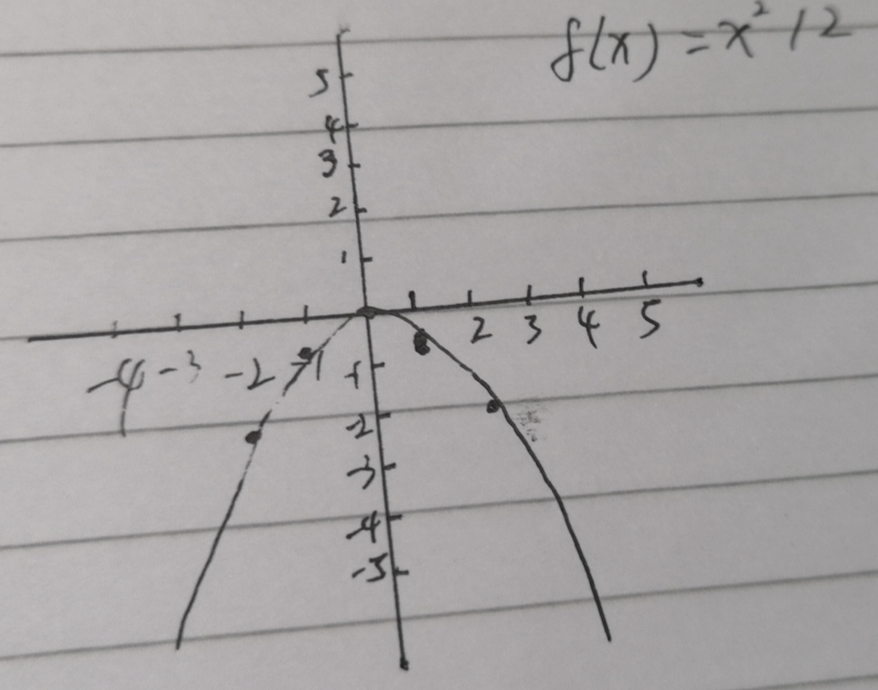
y会因为除以2变得更小（想象一下两侧的y值会变小），当x = 2 , y就会等于2, 这样的结果是曲线变宽。
那么我们也可以知道 如果 换成 f(x) = x^2 * 2, 当x=2，y等于4，曲线会变窄。
如果除以的数变成了负数，开口就会向下。
由上面我们可以得到一个可以控制曲线开口大小的函数
也可以换算到 f(x) = x^2 / t 当t 大于0，曲线开口向上，t小于0，曲线开口向下
左右偏移控制
现在我们可以控制开口大小，那么怎么样控制曲线左右移动呢？
假设左右偏移量是P
设函数 f(x) = (x - P)^2，P = 1 得到下面的表格：
| x= | -2 - 1 | -1 - 1 | 0 - 1 | 1 - 1 | 2 - 1 | 3 - 1 |
| y= | 9 | 4 | 1 | 0 | 1 | 4 |
还是用图像，大概长这样：
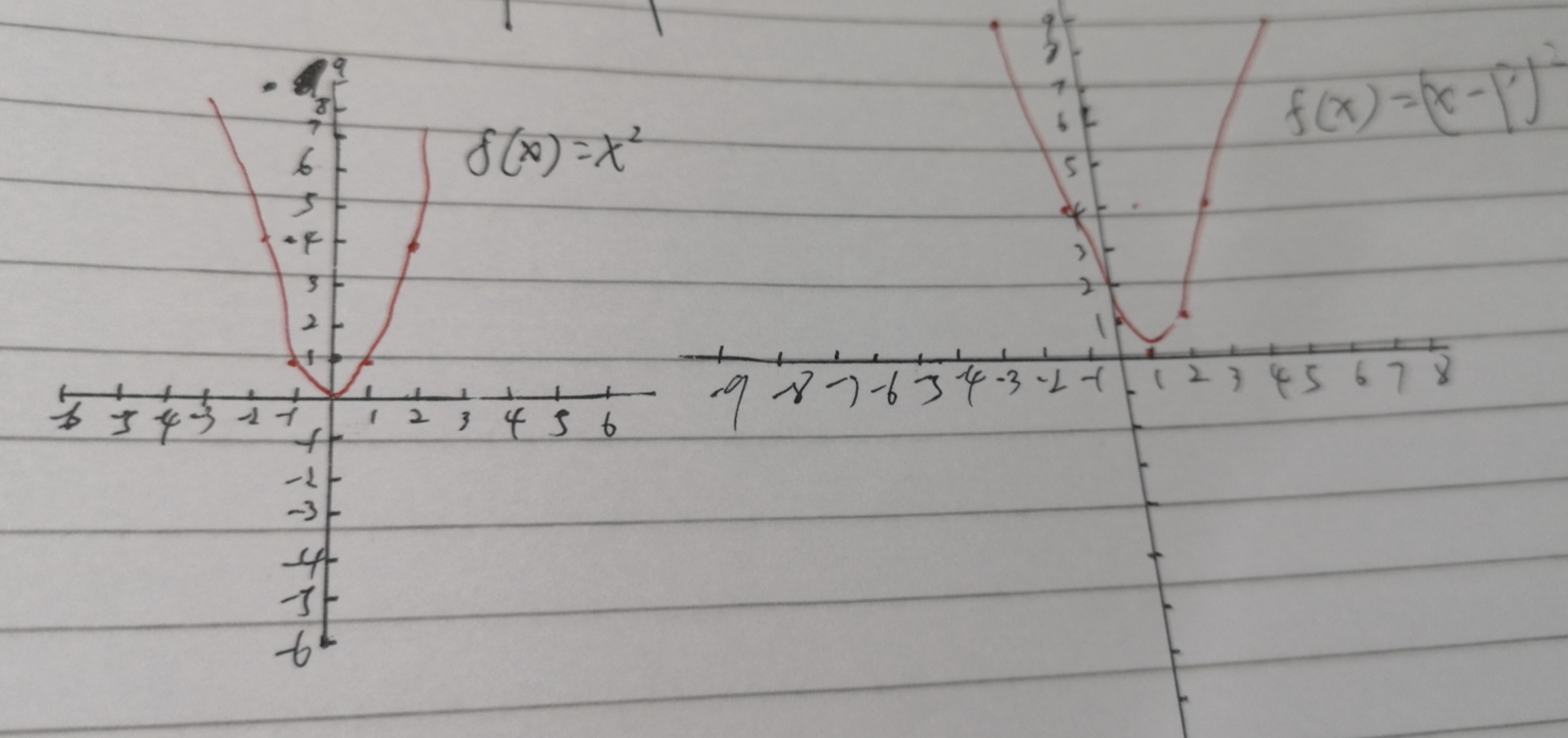
可以看到，P的取值影响图像的左右偏移
上下偏移控制
控制上下偏移，实际上就是控制函数 f(x) = x ^2的值y的大小，只需要将 f(x) = x ^2 - H 就可以控制上下啦
假设上下偏移量是H
设函数 f(x) = x^2 + H，H = 1 得到下面的表格：
| x= | -2 | -1 |
0 |
1 |
2 |
... |
| y= | 5 | 2 | 1 | 2 | 4 | ... |
图就不画啦，可以直接看到x=0时，顶点已经不再0上了，向上偏移了1位
值域区间和宽度的关系
什么是区间
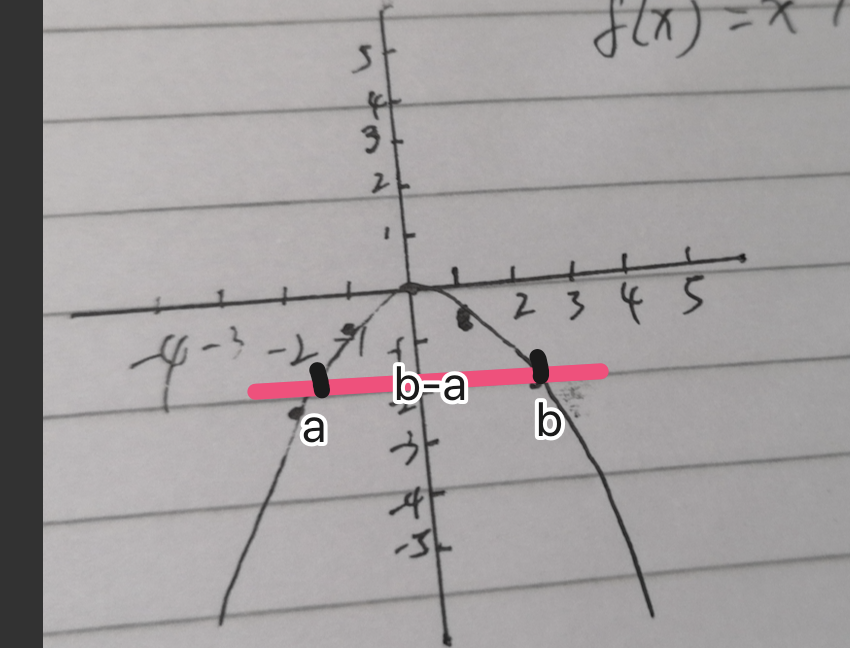
好了，理解了上面的东西，万事俱备，接下来就是更复杂一点的问题了！
接下来，工程问题，曲线
目标，使用函数
实现开头引用文章中，利用 cos和sin实现的曲线。
分析
通过上面对函数的分析我们可以得到一个式子：
设 抛物线开口 = T
设 左右偏移 = P
设 上下偏移 = H
设 定义域 = [a, b] （开区间a到开区间b）
函数 f(x) = (x - P) ^ 2 / T - H, T > 0 开口向上
函数g(x) = (x - P) ^ 2 / (T) - H, T < 0 开口向下
现在我们要使弧线A的结束点是弧线B的起始点，并且调换方向，那么：
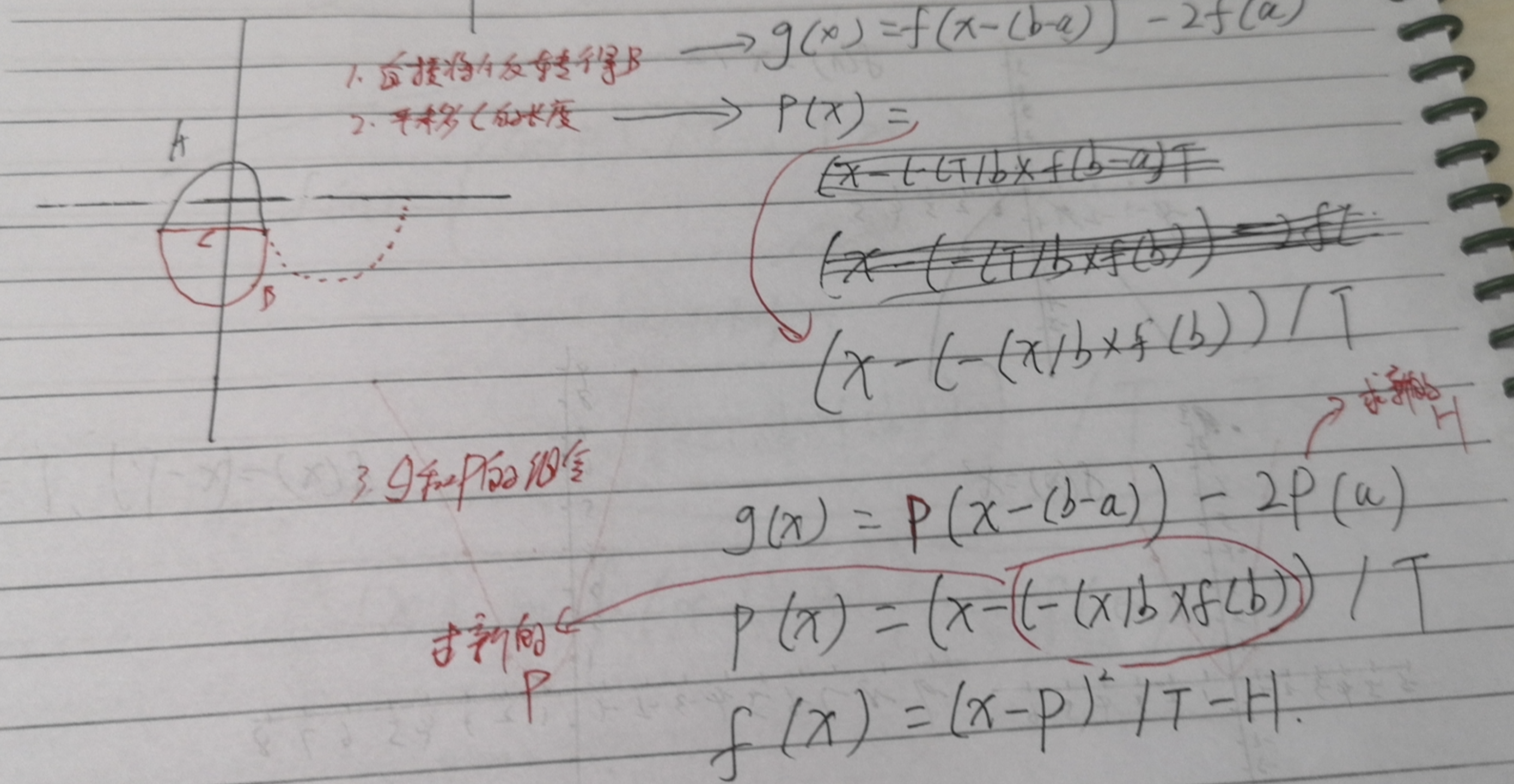
如图的推理过程，首先反转A，将A向下移动H,再向左移动P，得到一个新的弧度，以此类推递归：
然后用js实现一个简单的算法如下：
// g(x) = f(x-(b-a)) - 2* f(a)， T < 0
function g (x, T, P, range) {
const [a, b] = range
return f(x - (b - a), T, P, range) - 2 * f(0, T, P, range)
} // 当 T < 0 相当于上面图中的 p(x) = (x - (- (T / B * f(b - a)))) / T， T < 0
// 当 T > 0 直接计算 f(x) = (x - P) ^ 2 / T, T > 0
function f (x, T, P, range, s) {
const [a, b] = range
if (T < 0 && !s) {
return Math.pow(x - (-(T / b * f(b - a, T, P, range, true))), 2) / T
}
if (T > 0 || s) {
return Math.pow(x - P, 2) / T
} }
// 选择初始函数
function getY (x, T, P, range) {
if (T > 0) {
return f(x, T, P, range)
} else {
return g(x, T, P, range)
}
}
//获取一堆x，y点组成的集合， size = 波浪数量，origin=原点，item = 配置P H T变量，points和ysize为递归存储数据
function GetPoints(size, origin, item, points = [], ysize) {
if (ysize === undefined) {
ysize = size
}
if (size <= 0) {
return points
}
const z = size % 2 === 0
const M = 1 // 密度
const width = item.b - item.a // 宽度
let i = width;
while (i >= -width) {
const point = [
(origin[0] + i) + (ysize - size) * (width * 2), // x
origin[1] + getY(i, (z ? item.T : -item.T), item.P, [ // y
item.a,
item.b
])
]
points.push(point)
i -= M;
}
GetPoints(size-1, origin, {
a: item.a,
b: item.b,
T: item.T,
P: item.P
}, points, ysize)
return points;
}
效果
通过一连串懵逼式的计算和换算，我们有了一个可以获取固定数量相连的曲线，通过T控制开口，P控制x偏移，定义域[a,b]控制宽度,我们来实现骚操作：
拉到本地跑一跑：
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<meta http-equiv="X-UA-Compatible" content="ie=edge">
<title>Document</title>
<style>
.circle {
position: absolute;
width: 1px;
height: 1px;
background: #333;
border-radius: 50%;
left: 0px;
top: 0px;
transition: all 200ms;
}
</style>
</head>
<body>
<div class="circle" id="circle"></div>
<script>
function g (x, T, P, range) {
const [a, b] = range
return f(x - (b - a), T, P, range) - 2 * f(0, T, P, range)
} function f (x, T, P, range, s) {
const [a, b] = range
if (T < 0 && !s) {
return Math.pow(x - (-(T / b * f(b - a, T, P, range, true))), 2) / T
}
if (T > 0 || s) {
return Math.pow(x - P, 2) / T
} } function getY (x, T, P, range) {
if (T > 0) {
return f(x, T, P, range)
} else {
return g(x, T, P, range)
}
}
function GetPoints(size, origin, item, points = [], ysize) {
if (ysize === undefined) {
ysize = size
}
if (size <= 0) {
return points
}
const z = size % 2 === 0
const M = 1 // 密度
const width = item.b - item.a // 宽度
let i = width;
while (i >= -width) {
const point = [
(origin[0] + i) + (ysize - size) * (width * 2), // x
origin[1] + getY(i, (z ? item.T : -item.T), item.P, [ // y
item.a,
item.b
])
]
points.push(point)
i -= M;
}
GetPoints(size-1, origin, {
a: item.a,
b: item.b,
T: item.T,
P: item.P
}, points, ysize)
return points;
} /**
* 生成box-shadow参数
*/
function getBoxShadow (color = '#333') {
let points = GetPoints(6, [500, 100], {
a : 0,
b : 100,
T : 200,
P : 0
}) // const s = []
const s = points.map((point) => `${point[0]}px ${point[1]}px 0 0 ${color}`)
return s.join(',')
} document.querySelector('#circle').style.cssText = `box-shadow: ${getBoxShadow()}; transform: rotate(90deg) translate(-500px, -500px)` </script>
</body>
</html>
一毛一样，大功告成。
展望
利用数学函数，我们也可以画出使用sin / cos一毛一样的曲线，更多的，我们也可以用它来描绘一个物体的运动动作，例如波浪运动，抛物线运动。
甚至可以用css画苦逼脸：
加点动画玩玩
延续
数学与编程，有时候真的是相依相承的东西。从工程的角度来说，数学和程序算法有非常重要的关系，推荐大家阅读《数学与泛型编程》（高效编程的奥秘），受益匪浅，感觉整个程序职业生涯有了一次很棒的升华！
完。
【前端】 在前端利用数学函数知识+box-shadow解波浪图形的更多相关文章
- [面试专题]前端需要知道的web安全知识
前端需要知道的web安全知识 标签(空格分隔): 未分类 安全 [Doc] Crypto (加密) [Doc] TLS/SSL [Doc] HTTPS [Point] XSS [Point] CSRF ...
- Web前端开发如何利用css样式来控制Html中的h1/h2/h3标签不换行
H1/H2/H3/H4标题标签常常使用在一个网页中唯一标题.重要栏目.重要标题等情形下. H1在一个网页中最好只使用一次,如对一个网页唯一标题使用.H2.H3.H4标签则可以在一个网页中多次出现, ...
- Myth – 支持变量和数学函数的 CSS 预处理器
Myth 是一个预处理器,有点类似于 CSS polyfill .Myth 让你写纯粹的 CSS,同时还让你可以使用类似 LESS 和 Sass 的工具.您仍然可以使用变量和数学函数,就像你在其它预处 ...
- 【python游戏编程之旅】第四篇---pygame中加载位图与常用的数学函数。
本系列博客介绍以python+pygame库进行小游戏的开发.有写的不对之处还望各位海涵. 在上一篇博客中,我们学习了pygame事件与设备轮询.http://www.cnblogs.com/msxh ...
- Web前端 Web前端和Web后端的区分
一.绪论 1. 前台:呈现给用户的视觉和基本的操作. 后台:用户浏览网页时,我们看不见的后台数据跑动.后台包括前端.后端. 前端:对应我们写的html.css.javascript 等网页语言作用在前 ...
- 【函数】Oracle函数系列（2）--数学函数及日期函数
[函数]Oracle函数系列(2)--数学函数及日期函数 1 BLOG文档结构图 2 前言部分 2.1 导读和注意事项 各位技术爱好者,看完本文后,你可以掌握如下的技能,也可以学到一些其它你所不 ...
- VB.NET函数——数学函数/字母串函数
一.数学函数 函数 说明 Abs (num) 取绝对值. Exp (num) 返回以e为底.以num为指数的值,如Exp(2)返回e^2值. Log (num) 返回参数num的自然对数值,为Doub ...
- .net表达式计算器（中缀表达式转后缀表达式，支持20多个数学函数，支持函数嵌套）
最近在网上查了一下表达工计算器的类库,发现Java版本的有一个比较成熟的叫W3EVal,好像是一个IBM工程师写的,.net就很少了(可能是我了解不够多),但投机取巧的实现思路有很多,比如: (1)将 ...
- Java开发笔记（十一）常见的数学函数
前面介绍了Java编程的四则运算,虽然提供了基础的加减乘除符号,但是数学上还有其它运算符号,包括四舍五入用到的约等号≍.求绝对值的“| |”.开平方的“√￣”,这些运算符形态各异,而且并非ASCII码 ...
随机推荐
- Unity混合天空盒
对于不同天气下天空盒的实现. 天空盒时通过天空盒材质更改实现的,新建材质,选择shader/skybox/6sided,然后添加六个天空盒贴图就可以实现天空盒,如果想实现天气变化则需要至少两套贴图,并 ...
- 第八篇 Flask中的蓝图
随着业务代码的增加,将所有代码都放在单个程序文件中,是非常不合适的.这不仅会让代码阅读变得困难,而且会给后期维护带来麻烦.如下示例:我们在一个文件中写入多个路由,这会使代码维护变得困难. 如图所示,如 ...
- (Java) byte[] 和 base64 字符串之间的转换
import org.apache.commons.codec.binary.Base64; public class UtilHelper { //base64字符串转byte[] public s ...
- js实现的几种继承方式
他山之石,可以攻玉,本人一直以谦虚的态度学他人之所长,补自己之所短,望各位老师指正! 拜谢 js几种继承方式,学习中的总结: 所谓的继承是为了继承共有的属性,减少不必要代码的书写 第一种:借用构造函数 ...
- 为什么磁盘慢会导致Linux负载飙升？
一.CPU利用率和负载率的区别 这里要区别CPU负载和CPU利用率,它们是不同的两个概念,但它们的信息可以在同一个top命令中进行显示.CPU利用率显示的是程序在运行期间实时占用的CPU百分比,这是对 ...
- Luogu P1816 忠诚
rmq模板题.用st表切一个. 关于st表的详解见我的博客:st表.树状数组与线段树 笔记与思路整理 题目描述 老管家是一个聪明能干的人.他为财主工作了整整10年,财主为了让自已账目更加清楚.要求管家 ...
- NOIP模拟 31
补坑 skyh又AK 赛时榜搜索我的姓: 下一条 ... 自闭了. (只是表达对B哥强烈的崇敬) (如果B哥介意我把名字贴出来请联系我删掉) T1一打眼,好像就一个gcd 康了眼大样例,觉得没啥问题 ...
- js清除节点内容（改变标签元素）
<!DOCTYPE HTML><html> <head> <meta http-equiv="Content-Type" c ...
- 帝国cms7.5免登陆发布模块
帝国cms7.5免登陆发布文章. 帝国cms增加了金刚模式,登录发布文章有难度.免登录发布模块配合火车采集器,完美解决你遇到的问题. 1.必备工具: 1.火车采集器 2.免登陆发布接口 3.帝国cms ...
- Windows键盘无法调起
Windows 键盘无法调起 经常使用触摸屏幕的小伙伴肯定都遇到过屏幕键盘怎么也唤不起来(在桌面模式下,非平板模式).以下收集了一些常见的解决方案: 注:本文基于 Windows 10 v1903,其 ...