Batch Normalization、Layer Normalization、Instance Normalization、Group Normalization、Switchable Normalization比较

深度神经网络难训练一个重要的原因就是深度神经网络涉及很多层的叠加，每一层的参数变化都会导致下一层输入数据分布的变化，随着层数的增加，高层输入数据分布变化会非常剧烈，这就使得高层需要不断适应低层的参数更新。为了训练好模型，我们需要谨慎初始化网络权重，调整学习率等。

本篇博客总结几种归一化办法，并给出相应计算公式和代码。

归一化层，目前主要有这几个方法，Batch Normalization（2015年）、Layer Normalization（2016年）、Instance Normalization（2017年）、Group Normalization（2018年）、Switchable Normalization（2018年）；

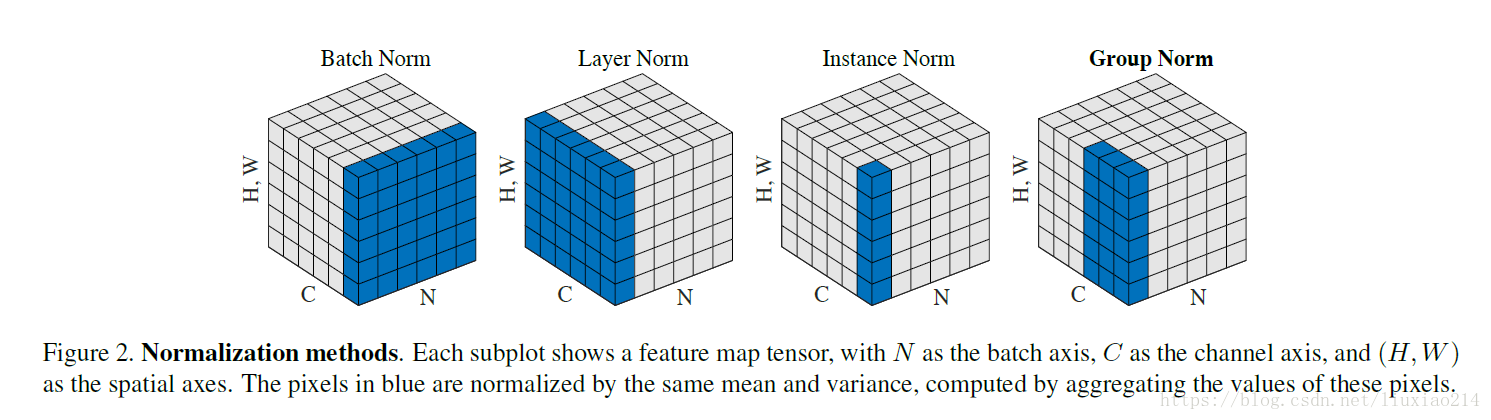
将输入的图像shape记为[N, Channel, Height, Width]，这几个方法主要的区别就是在，

• batch Norm：在batch上，对NHW做归一化，对小batchsize效果不好；
• layer Norm：在通道方向上，对CHW归一化，主要对RNN作用明显；
• instance Norm：在图像像素上，对HW做归一化，用在风格化迁移；
• Group Norm：将channel分组，然后再做归一化；
• Switchable Norm：将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。

那我们就看看下面的两个动图, 这就是在每层神经网络有无 batch normalization 的区别

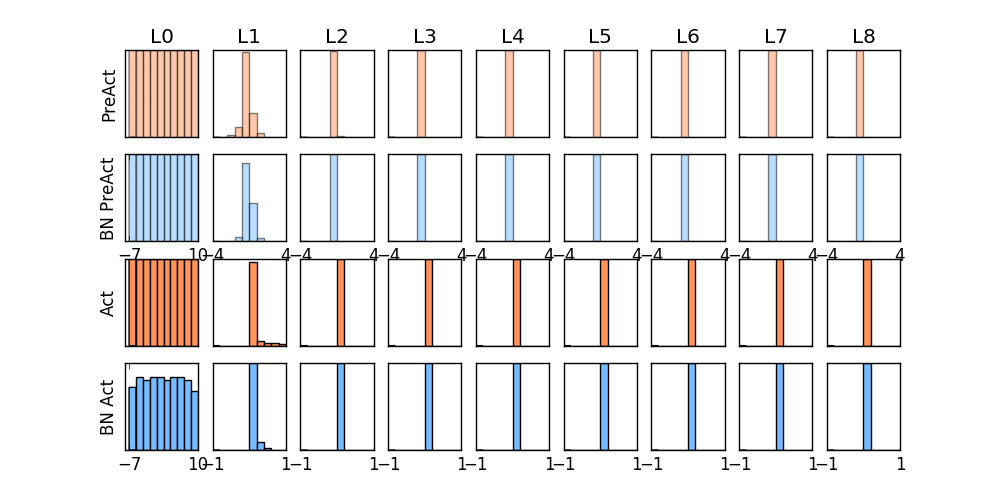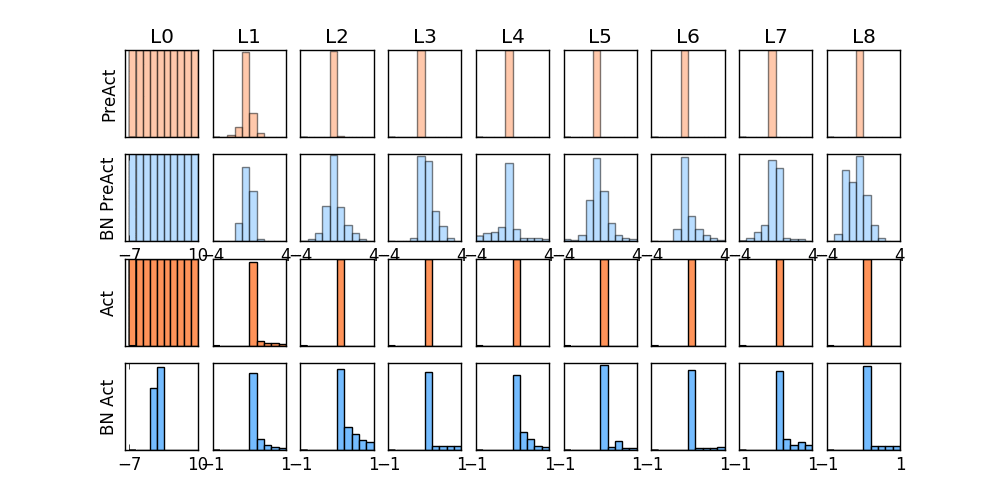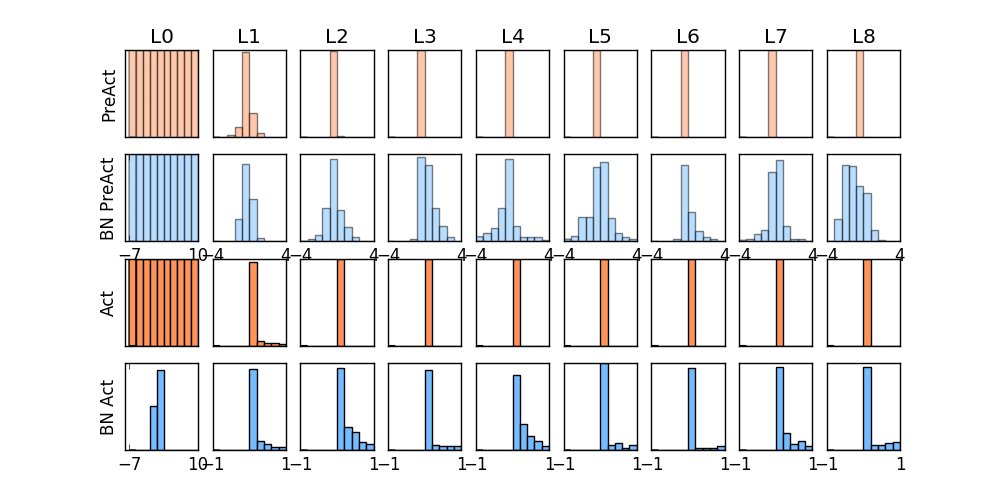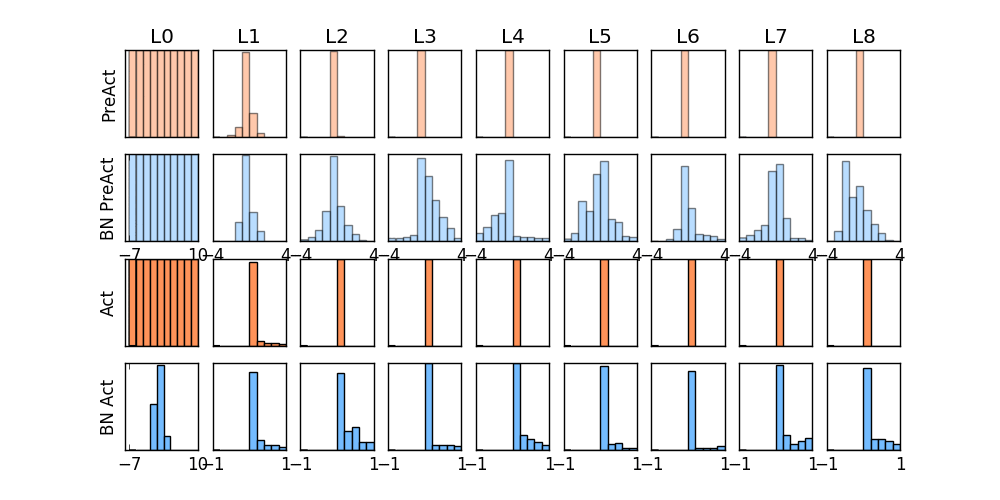
没有normalization 的输出数据很多都等于0，导致后面的神经元“死掉”，起不到任何作用。

Batch Normalization

　　首先，在进行训练之前，一般要对数据做归一化，使其分布一致，但是在深度神经网络训练过程中，通常以送入网络的每一个batch训练，这样每个batch具有不同的分布；而且在训练过程中，数据分布会发生变化，对下一层网络的学习带来困难。

　　batch normalization就是强行将数据拉回到均值为0，方差为1的正太分布上，这样不仅数据分布一致，而且避免发生梯度消失。保证每一次数据经过归一化后还保留原有学习来的特征，同时又能完成归一化操作，加速训练。

$$\mu=\frac{1}{m}\sum_{i=1}^mx_i$$

$$\sigma =\sqrt {\frac{1}{m}\sum_{i=1}^m(x_i-\mu)^2)}$$

$$y= \frac{(x-\mu)}{\sqrt{\sigma ^2+\epsilon }}+\beta =BN(x)$$

tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None)

参数

• x：输入数据
• mean：均值
• variance：方差

返回

• 标准化后的数据

Layer Normalizaiton

batch normalization存在以下缺点：

• 对batch size的大小比较敏感，由于每次计算均值和方差是在一个batch上，所以如果batch size太小，则计算的均值、方差不足以代表整个数据分布；
• BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用BN，很方便；但对于RNN来说，sequence的长度是不一致的，换句话说RNN的深度不是固定的，不同的time-step需要保存不同的statics特征，可能存在一个特殊sequence比其他sequence长很多，这样training时，计算很麻烦。

LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。

$$\mu^l=\frac{1}{H}\sum^H_{i=1}a_i^l$$

$$\sigma ^l=\sqrt {\frac{1}{H}\sum^H_{i=1}(a_i^l-\mu^l)^2}$$

BN与LN的区别在于：

• LN中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差；
• BN中则针对不同神经元输入计算均值和方差，同一个batch中的输入拥有相同的均值和方差。

所以，LN不依赖于batch的大小和输入sequence的深度，因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。

LN用于RNN效果比较明显，但是在CNN上，不如BN。

tf.keras.layers.LayerNormalization(axis=-1, epsilon=0.001, center=True, scale=True)

参数

• axis：想要规范化的轴（通常是特征轴）
• epsilon：将较小的浮点数添加到方差以避免被零除。
• center：如果为True，则将的偏移beta量添加到标准化张量。
• scale：如果为True，则乘以gamma

返回

• shape与输入形状相同的值

Instance Normalization

　　BN注重对每个batch进行归一化，保证数据分布一致，因为判别模型中结果取决于数据整体分布。

　　但是图像风格化中，生成结果主要依赖于某个图像实例，所以对整个batch归一化不适合图像风格化中，因而对HW做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。

$$\mu_{ti}=\frac{1}{HW}\sum_{l=1}^{W}\sum_{m=1}^{H}x_{tilm}$$

$$\sigma =\sqrt{\frac{1}{HW}\sum_{l=1}^{W}\sum_{m=1}^{H}(x_{tilm}-\mu_{yi})^2}$$

$$y_{tijk}=\frac{x_{Ptijk}-\mu_{yi}}{\sqrt {\sigma ^2_{ti}}-\epsilon }$$

tfa.layers.normalizations.InstanceNormalization

输入：仅在该层只有一个输入（即，它连接到一个传入层）时适用。

返回：输入张量或输入张量列表。

def Instancenorm(x, gamma, beta):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(2, 3), keepdims=True)
    x_var = np.var(x, axis=(2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

Group Normalization

主要是针对Batch Normalization对小batchsize效果差，GN将channel方向分group，然后每个group内做归一化，算(C//G)*H*W的均值，这样与batchsize无关，不受其约束。

$$S_i=\{k|k_N=i_N,[\frac{k_C}{C/G}]=[\frac{i_C}{C/G}]\}$$

def GroupNorm(x, gamma, beta, G=16):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5
    x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))

    x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)
    x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

Switchable Normalization

本篇论文作者认为，

• 第一，归一化虽然提高模型泛化能力，然而归一化层的操作是人工设计的。在实际应用中，解决不同的问题原则上需要设计不同的归一化操作，并没有一个通用的归一化方法能够解决所有应用问题；
• 第二，一个深度神经网络往往包含几十个归一化层，通常这些归一化层都使用同样的归一化操作，因为手工为每一个归一化层设计操作需要进行大量的实验。

因此作者提出自适配归一化方法——Switchable Normalization（SN）来解决上述问题。与强化学习不同，SN使用可微分学习，为一个深度网络中的每一个归一化层确定合适的归一化操作。

$$\hat{h}_{hcij}=\gamma \frac{h_{hcij}-\sum_{k\epsilon \Omega W_k\mu_k}}{\sqrt {\sum_{k\epsilon \Omega}w'_k\sigma _k^2+\epsilon }}+\beta $$

$$w_k=\frac{e^{\lambda _k}}{\sum_{z\epsilon \{in,ln,bn\}e^{\lambda _z}}},\quad k\in \{in,ln,bn\}$$

$$\mu_{in}=\frac{1}{HW}\sum_{i,j}^{H,W}h_{ncij},\quad \sigma ^2=\frac{1}{HW}\sum_{i,j}^{H,W}(h_{ncij}-\mu_{in})^2$$

$$\mu_{ln}=\frac{1}{C}\sum_{c=1}^{C}\mu_{in},\quad \sigma ^2_{ln}=\frac{1}{C}\sum_{c=1}^{C}(\sigma^2 _{in} +\mu ^2_{in})-\mu^2_{ln}$$

$$\mu_{bn}=\frac{1}{N}\sum_{n=1}^{N}\mu_{in},\quad \sigma ^2=\frac{1}{N}\sum_{n=1}^{N}(\sigma _{in}^2+\mu_{in}^2)-\mu_{bn}^2$$

def SwitchableNorm(x, gamma, beta, w_mean, w_var):
    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    mean_in = np.mean(x, axis=(2, 3), keepdims=True)
    var_in = np.var(x, axis=(2, 3), keepdims=True)

    mean_ln = np.mean(x, axis=(1, 2, 3), keepdims=True)
    var_ln = np.var(x, axis=(1, 2, 3), keepdims=True)

    mean_bn = np.mean(x, axis=(0, 2, 3), keepdims=True)
    var_bn = np.var(x, axis=(0, 2, 3), keepdims=True)

    mean = w_mean[0] * mean_in + w_mean[1] * mean_ln + w_mean[2] * mean_bn
    var = w_var[0] * var_in + w_var[1] * var_ln + w_var[2] * var_bn

    x_normalized = (x - mean) / np.sqrt(var + eps)
    results = gamma * x_normalized + beta
    return results

结果比较

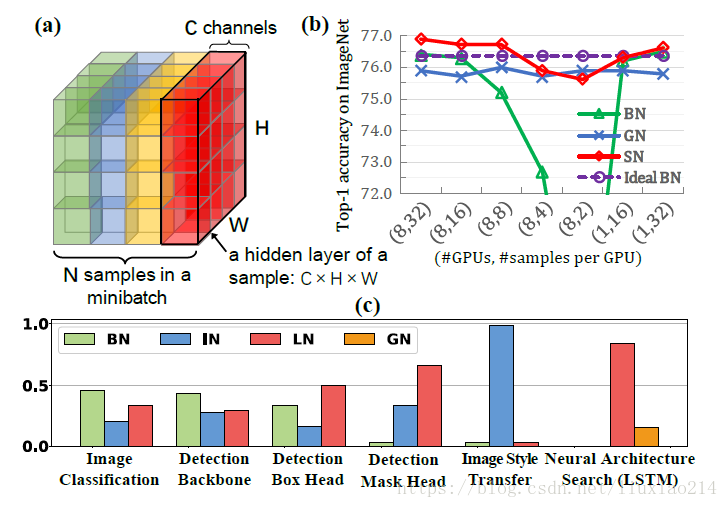
参考

CSDN博客总结可归一化方法并给出了numpy实现代码