HDU- 6437.Videos 最“大”费用流 -化区间为点

参考和完全学习：http://www.cnblogs.com/xcantaloupe/p/9519617.html

HDU-6437

题意：

　　有m场电影，电影分为两种，看一场电影可以得到对应的快乐值。有k个人，一场电影只能一个人参加，并且如果时间允许可以连续观看，但是如果连续看的电影是同一类型的，就要把快乐值减去一个w，这个w是累计的。问如何安排，可以使得k个人的快乐值最大。

思路:

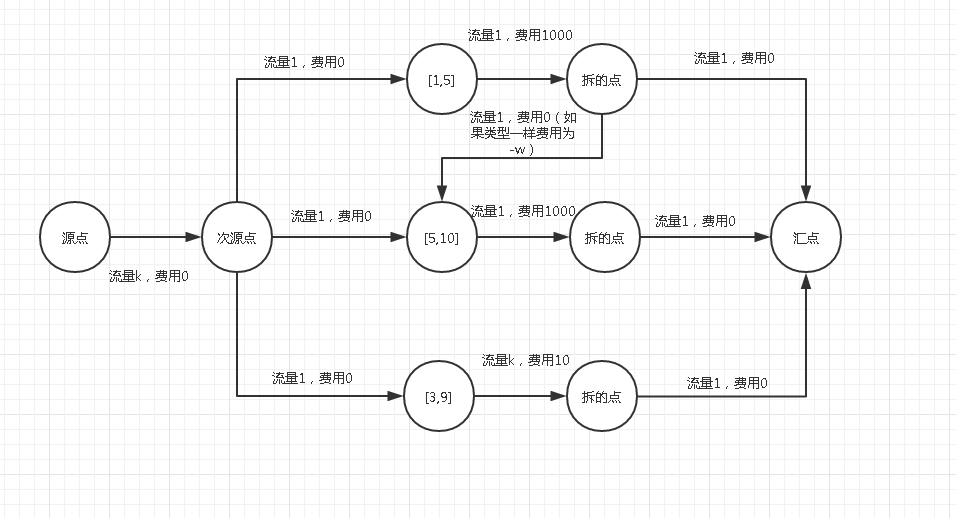
　　网络流问题建图真难。可以给每部电影当成一个点i，连一条从i到i+m 的边，容量为1，花费为对应的快乐值*-1，因为要求的是最大的“花费”，所以取反。再枚举点，如果时间允许，从i+m到j连一条边，若 i 和 j 类型相同，花费为w，否则为0。

这里把0点当做超级源点，m+m+1当做源点，从超级大源点到源点有k的容量，把m+m+2当做终点，就可以建图成功了。

　　（参考里拿的图）

#include <algorithm>
#include  <iterator>
#include  <iostream>
#include   <cstring>
#include   <iomanip>
#include   <cstdlib>
#include    <cstdio>
#include    <string>
#include    <vector>
#include    <bitset>
#include    <cctype>
#include     <queue>
#include     <cmath>
#include      <list>
#include       <map>
#include       <set>
using namespace std;
//#pragma GCC optimize(3)
//#pragma comment(linker, "/STACK:102400000,102400000")  //c++
#define lson (l , mid , rt << 1)
#define rson (mid + 1 , r , rt << 1 | 1)
#define debug(x) cerr << #x << " = " << x << "\n";
#define pb push_back
#define pq priority_queue

typedef long long ll;
typedef unsigned long long ull;

typedef pair<ll ,ll > pll;
typedef pair<int ,int > pii;
typedef pair<int ,pii> p3;
//priority_queue<int> q;//这是一个大根堆q
//priority_queue<int,vector<int>,greater<int> >q;//这是一个小根堆q
#define fi first
#define se second
//#define endl '\n'

#define OKC ios::sync_with_stdio(false);cin.tie(0)
#define FT(A,B,C) for(int A=B;A <= C;++A)  //用来压行
#define REP(i , j , k)  for(int i = j ; i <  k ; ++i)
//priority_queue<int ,vector<int>, greater<int> >que;

const ll mos = 0x7FFFFFFFLL;  //
const ll nmos = 0x80000000LL;  //-2147483648
const int inf = 0x3f3f3f3f;
const ll inff = 0x3f3f3f3f3f3f3f3fLL; //
const double PI=acos(-1.0);

template<typename T>
inline T read(T&x){
    x=;int f=;char ch=getchar();
    while (ch<''||ch>'') f|=(ch=='-'),ch=getchar();
    while (ch>=''&&ch<='') x=x*+ch-'',ch=getchar();
    return x=f?-x:x;
}
// #define _DEBUG;         //*//
#ifdef _DEBUG
freopen("input", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
/*-----------------------show time----------------------*/

        const int maxn = 1e5+;

        struct Edge
        {
            int to,val,cost,nxt;
        }gEdge[maxn];
        int gHead[maxn],gPre[maxn];
        int gPath[maxn],gDist[maxn];
        bool in[maxn];
        int gcount = ;
        int n,m,k,w;

        bool spfa(int s,int t){

            memset(gPre, -, sizeof(gPre));
            memset(gDist,inf,sizeof(gDist));
            memset(in, false , sizeof(in));
            gDist[s] = ; in[s] = true;
            queue<int>q;
            q.push(s);
            while(!q.empty()){
                int u = q.front();
                q.pop();    in[u] = false;
                for(int e = gHead[u]; e!=-; e = gEdge[e].nxt){
                    int v = gEdge[e].to, w = gEdge[e].cost;
                    if(gEdge[e].val >  && gDist[v] > gDist[u] + w){
                        gDist[v] = gDist[u] + gEdge[e].cost;
                        gPre[v] = u;
                        gPath[v] = e;
                        if(!in[v]){
                            q.push(v);in[v] = true;
                        }
                    }
                }
            }
            if(gPre[t] == -)return false;
            return true;
        }
        int MinCostFlow(int s,int t){
            int cost = ,flow = ;
            while(spfa(s,t)){
                int f = inf;
                for(int u = t; u != s; u = gPre[u]){
                    if(gEdge[gPath[u]].val < f){
                        f =gEdge[gPath[u]].val;
                    }
                }
                flow += f;
                cost += gDist[t] * f;
                for(int u=t; u!=s; u = gPre[u]){
                    gEdge[gPath[u]].val -= f;
                    gEdge[gPath[u] ^ ].val += f;
                }
            }
            return cost;
        }

        void addedge(int u,int v,int val, int cost){
            gEdge[gcount].to = v;
            gEdge[gcount].val = val;
            gEdge[gcount].cost = cost;
            gEdge[gcount].nxt = gHead[u];
            gHead[u] = gcount++;

            gEdge[gcount].to = u;
            gEdge[gcount].val = ;
            gEdge[gcount].cost = -cost;
            gEdge[gcount].nxt = gHead[v];
            gHead[v] = gcount++;

        }

        struct eee
        {
            int l,r,w,op;
        }e[maxn];
        /*
            0 是大源点，m+m+1是ci源点，m+m+2是终点。
        */
        void solve(){
                    memset(gHead,-,sizeof(gHead));
                    gcount = ;
                    scanf("%d%d%d%d", &n, &m, &k, &w);
                    addedge(,m+m+,k,);
                    for(int i=; i<=m; i++){
                        scanf("%d%d%d%d", &e[i].l, &e[i].r, &e[i].w, &e[i].op);
                    }

                    for(int i=; i<=m; i++){
                        for(int j=; j<=m; j++){
                            if(i==j)continue;

                            if(e[i].r <= e[j].l){
                                int tmp;
                                if(e[i].op == e[j].op)tmp = w;
                                else tmp = ;
                                addedge(i+m,j,,tmp);
                            }
                        }
                    }

                    for(int i=; i<=m; i++){
                        addedge(i,i+m,,-e[i].w);
                        addedge(i+m, m+m+,,);
                        addedge(m+m+, i,,);
                    }
                    printf("%d\n",-*MinCostFlow(,m+m+));
        }
int main(){
        int T;  scanf("%d", &T);
        while(T--){
            solve();
        }
        return ;
}

HDU-6437