Table.LastN保留后面N….Last…（Power Query 之 M 语言）

数据源：

“姓名”“基数”“个人比例”“个人缴纳”“公司比例”“公司缴纳”“总计”，共7列5行数据

目标：

只留下后面两行数据（删除掉前面三行）

操作过程：

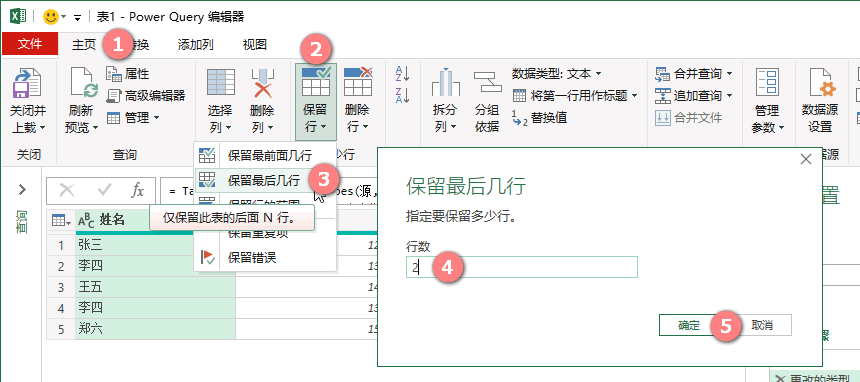
【主页】》【保留行】》【保留最后几行】》输入保留的行数》【确定】

　　

M公式：

保留行：= Table.LastN( 表, 保留的行数或条件)

说明：

　　同保留前面N行Table.FirstN

最终效果：

数据只剩下后两行

扩展：

　　列表中保留后面N项：= List.LastN( 列表, 保留的项数或条件)

　　　　示例：=List.LastN({1..10}, each _ >5)

　　　　结果：保留列表中的后5项，即{6,7,8,9,10}

　　表最后一行转成记录：=Table.Last( 表, 列表)

　　　　如果表为空，则返回第二参数中的列表所转成的记录

　　列表最后一项转成单个的值：=List.Last( 列表, 值)

　　　　如果列表为空，则返回第二参数中的值，这个值可以是任意数据类型