[题解]第十一届北航程序设计竞赛预赛——F.序列

题目描述

(1,……,n)的一个排列S，定义其对应的权值F[S]为：将S划分为若干段连续子序列，每个子序列都是上升序列，F[S]的值等于能划分出的最小段数。

求n的全排列的F[S]的和，答案mod(10^9+7)。

解题思路

刚拿到题目时，我没什么思路，于是决定列举情况找找规律。

当n == 1时，F[1] = 1，结论是平凡的。

当n == 2时，全排列如下：

(1，2)：1个子序列

(2，1)：2个子序列

可以得出F[2] = 3。

当n == 3时，考虑在n == 2的情况下插入数字3。

（1）将3插入到第一个位置，得到排列：

(3，1，2)：2个子序列

(3，2，1)：3个子序列

相比插入前，每个排列的序列数+1。

（2）将3插入到第二个位置，得到排列：

(1，3，2)：2个子序列

(2，3，1)：2个子序列

相比插入前，1个排列的序列数+1，1个排列的序列数不变。

（3）将3插入到第三个位置，得到排列：

(1，2，3)：1个子序列

(2，1，3)：2个子序列

相比插入前，每个排列的序列数不变。

综上，可以得出F[3] = 12。

当n==4时，与之前相似的思路，插入数字4。

（1）将4插入到第一个位置，得到排列：

(4，3，1，2)：3个子序列

(4，3，2，1)：4个子序列

(4，1，3，2)：3个子序列

(4，2，3，1)：3个子序列

(4，1，2，3)：2个子序列

(4，2，1，3)：3个子序列

相比插入前，每个排列的序列数+1。

（2）将4插入到第二个位置，得到排列：

(3，4，1，2)：2个子序列

(3，4，2，1)：3个子序列

(1，4，3，2)：3个子序列

(2，4，3，1)：3个子序列

(1，4，2，3)：2个子序列

(2，4，1，3)：2个子序列

相比插入前，3个排列的序列数+1，3个排列的序列数不变。

（3）将4插入到第三个位置，得到排列：

(3，1，4，2)：3个子序列

(3，2，4，1)：3个子序列

(1，3，4，2)：2个子序列

(2，3，4，1)：2个子序列

(1，2，4，3)：2个子序列

(2，1，4，3)：3个子序列

相比插入前，3个排列的序列数+1，3个排列的序列数不变。

（4）将4插入到第四个位置，得到排列：

(3，1，2，4)：2个子序列

(3，2，1，4)：3个子序列

(1，3，2，4)：2个子序列

(2，3，1，4)：2个子序列

(1，2，3，4)：1个子序列

(2，1，3，4)：2个子序列

相比插入前，每个排列的序列数不变。

综上，可以得出F[4] == 60。

这时我们可以发现：F[n + 1] = (F[n] + n!) + (F[n] + n!/2) + ……+ (F[n] + n!/2) + (F[n]) = (n + 1) * F[n] + (n + 1)!/2

即：F[n] = (n + 1)!/2

在比赛现场我没有证明，但根据上述思路，可以利用排列组合给出简单的证明。

于是问题转化为求阶乘除以2后模大数取余。

这里用到了同余的性质：

（1）x≡a(mod m)且y≡b(mod m)，则x+y≡a+b(mod m)；

（2）x≡a(mod m)且y≡b(mod m)，则x-y≡a-b(mod m)；

（3）x≡a(mod m)且y≡b(mod m)，则xy≡ab(mod m)。

所以我们想到，(n + 1)!可以每乘以一个因子就取一次模。这里有个很重要的细节，同余对除法没有这么好的性质，不能算完(n + 1)! mod 10^9+7后再除以2，这样答案是错误的。所以我们采用一开始就除以二的方式开始计算。

附：c++代码

 1 #include <iostream>
 2 #include <cstdio>
 3
 4 using namespace std;
 5 #define MOD 1000000007LL
 6 #define MaxN 100020
 7
 8 typedef long long llt;
 9
10 llt J[MaxN];
11
12 inline void Get_J()
13 {
14     llt i;
15     J[0] = J[1] = 1;
16     J[2] = 1;
17     for(i = 3; i <= 100001; i++)
18         J[i] = (J[i - 1] * i) % MOD;
19 }
20
21 int main()
22 {
23     llt i, n;
24     // ans;
25     //llt N = 1;
26     //J[0] = J[1] = 1;
27     Get_J();
28     while(scanf("%lld", &n) != EOF)
29     {
30         //ans = J[n + 1] / 2;
31         printf("%lld\n", J[n + 1]);
32     }
33     return 0;
34 }

另一种思路

这是官方给出的题解。

对于一个固定的排列p，权值为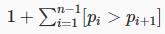。所以相邻两个数字，如果前面数字大于后面数字则对答案贡献1。

公式：。

题目链接：https://biancheng.love/contest-ng/index.html#/29/problems