Solution -「HNOI 2009」「洛谷 P4727」图的同构计数

\(\mathcal{Description}\)

  Link.

  求含 \(n\) 个点的无标号简单无向图的个数，答案模 \(997\)。

\(\mathcal{Solution}\)

  首先，把题目转化成为有标号 \(K_n\) 的 \(\binom{n}{2}\) 条边染黑（不选）白（选）两种颜色，求本质不同（去除标号）的方案数。想到使用 Pólya 定理求解。设在某个点转置中，循环大小为 \(a_1,a_2,\cdots,a_k\)，分别考虑循环内部和循环间的边等价类：

  对于大小为 \(a\) 的循环内部，仍旧是一个 \(K_a\)，尝试求其中边等价类的个数，例如 \(a=6\)，如图（来自 @pythoner713 的博客，下图同）：

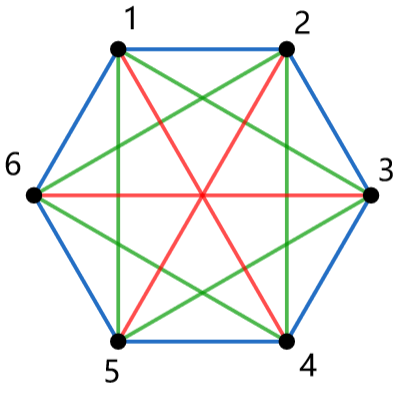
可见共红色、绿色、蓝色三个等价类。进一步，若把 \(K_a\) 画作类似的正多边形，发现边属于同一等价类当且仅当它们长度相等，继而得出大小为 \(a\) 的循环的等价类个数为 \(\lfloor\frac{a}{2}\rfloor\)。

  对于两个大小分别为 \(a,b\) 的循环之间，考虑转置它们直到与初始状态重合，如图：

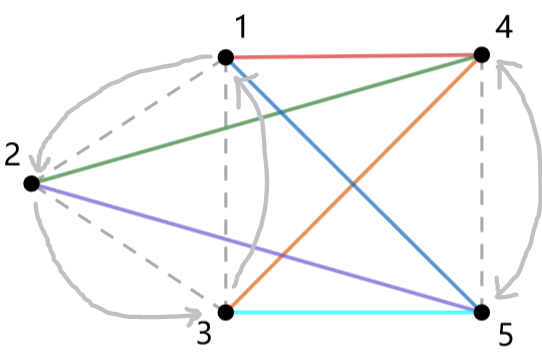
循环大小为 \(\operatorname{lcm}(a,b)\)，那么共 \(\gcd(a,b)\) 个等价类。

  综上，符合 \(\{a_k\}\) 所描述的转置的等价类个数 \(c(a)\) 为

\[\sum_{i=1}^k\lfloor\frac{a_i}{2}\rfloor+\sum_{1\le i<j\le k}\gcd(a_i,a_j)
\]

  考虑直接枚举 \(\{a_k\}\)，则符合条件的转置方案数为

\[\frac{n!}{\prod_{i=1}^ka_i\prod_{i=1}^nb_i}
\]

其中 \(b_i=\sum_{j=1}^k[a_j=i]\)，即大小为 \(i\) 的循环个数。组合意义为：在所有转置中，固定每个循环的第一个元素，再去除等大循环的顺序。

  最终方案数为

\[\frac{1}{n!}\sum_{\{a_k\}}2^{c(a)}\frac{n!}{\prod_{i=1}^ka_i\prod_{i=1}^nb_i}\\=\sum_{\{a_k\}}2^{c(a)}\left(\prod_{i=1}^ka_i\prod_{i=1}^nb_i\right)^{-1}
\]

拆分 \(n\) 求解即可，复杂度见 A296010。

\(\mathcal{Code}\)

/* Clearink */

#include <cstdio>

#define rep( i, l, r ) for ( int i = l, rep##i = r; i <= rep##i; ++i )
#define per( i, r, l ) for ( int i = r, per##i = l; i >= per##i; --i )

const int MOD = 997, MAXN = 60;
int n, fac[MAXN + 5];

inline int gcd( const int a, const int b ) { return b ? gcd( b, a % b ) : a; }
inline int mul( const long long a, const int b ) { return int( a * b % MOD ); }
inline int add( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline void addeq( int& a, const int b ) { ( a += b ) >= MOD && ( a -= MOD ); }
inline int mpow( int a, int b ) {
	int ret = 1;
	for ( ; b; a = mul( a, a ), b >>= 1 ) ret = mul( ret, b & 1 ? a : 1 );
	return ret;
}

int a[MAXN + 5], ans, t;

inline int calc() {
	t += a[0] * a[0];
	int s = 1;
	for ( int l = 1, r; l <= a[0]; l = r ) {
		for ( r = l; r <= a[0] && a[l] == a[r]; ++r );
		s = mul( s, fac[r - l] );
	}

	int idx = 0;
	rep ( i, 1, a[0] ) {
		idx += a[i] >> 1, s = mul( s, a[i] );
		rep ( j, i + 1, a[0] ) idx += gcd( a[i], a[j] );
	}

	return mul( mpow( s, MOD - 2 ), mpow( 2, idx ) );
}

inline void split( const int x, const int rest ) {
	if ( !rest ) return addeq( ans, calc() );
	if ( rest < x ) return ;
	split( x + 1, rest );
	a[++a[0]] = x, split( x, rest - x ), --a[0];
}

int main() {
	scanf( "%d", &n );

	fac[0] = 1;
	rep ( i, 1, n ) fac[i] = mul( i, fac[i - 1] );

	split( 1, n );

	printf( "%d\n", t );
	return 0;
}