求解Ax=b

一 线性方程组 Ax=b 的解释

线性方程组 Ax=b，其中矩阵 A 尺寸为 m*n, 当 A 为方正时，可使用消元法判断解是否存在并求解。当 A 为长方形矩阵时，同样可使用消元法判断解存在情况并求解。

线性方程组 Ax=b 可以使用不同观点看待：

1）可看作函数 f(x)=b,即输入任意 n 维向量 x，经过矩阵 A 变换处理，输出 m 维向量 b，即向量 b 由向量 x 通过矩阵 A 线性变换得到；

2）令 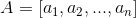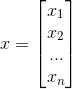， ，Ax=b 可表示为 ，

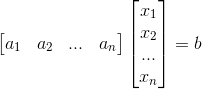进一步改写得 ，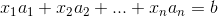

当 b 是矩阵 A 列向量 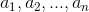 的线性组合时，或者 b 在矩阵 A 列空间时，Ax=b 可解，否则 Ax=b 不可解；

3）当矩阵 A 存在左逆 B 时，BA=I，则有 BAx=Bb，x=Bb；当矩阵A存在右逆 C 时，AC=I， 则有 Ax=ACb，x=Cb；

求解线性方程组转换为求矩阵 A 是否存在左逆或者右逆，以及其逆是否唯一；

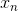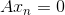4）当向量  满足   时，则向量 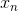 位于矩阵 A 的零空间，令  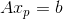为 Ax=b 的一个特解，则有  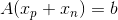成立，也即 Ax=b 的解为 ；

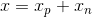  二 矩阵 A 的四个子空间

考虑矩阵 A 为 m*n，该矩阵由 n 个 m 维列向量构成，

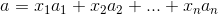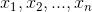1）对 n 个列向量进行任意线性组合 ， 其中  为任意实数序列，则向量 a 构成的集合为矩阵 A 的列空间，表示为 C(A)；

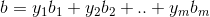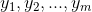2）对 m 个行向量进行线性组合 ，其中  为任意实数序列，则向量 b 构成的集合为矩阵 A 的行空间，表示为 ；

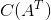3）求解 Ax=0，解 x 构成的集合为矩阵 A 的零空间，表示为 N(A)；矩阵 A 的行空间与矩阵 A 的零空间为 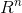 下相互正交的子空间；

观察方程组 Ax=0 表示为矩阵 A 每一行与向量 x 点积为零，则任意行空间中向量与任意零空间中向量点积为零，表明两个子空间正交；

4）求解 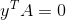，解 y 构成的集合为矩阵 A 的左零空间，表示为 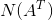；矩阵 A 的列空间与矩阵 A 的左零空间为  下相互正交的子空间；

观察方程组 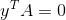 表示为向量 y 与矩阵 A 的每一列点积为零，则任意左零空间的向量与任意列空间中的向量点积为零，表明两个子空间正交；

以上给出矩阵 A 的四个子空间，通过高斯消元法将矩阵 A 化为 U（反向消元可进一步化为 R），可以得到矩阵 A 的四个子空间的维度，以及各个子空间的基。

下面通过一个矩阵实例求解矩阵各个子空间得维度与基。

设矩阵 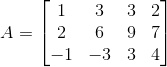，使用高斯消元法得 ，

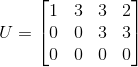消元中间变量 , ，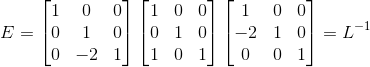

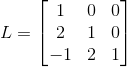同样，对于长方形矩阵，A=LU 成立。观察矩阵列，可以清楚主元位于列一与列三上，即矩阵得秩等于 2。同样，观察矩阵行，只有两行非零向量。

由于矩阵消元是针对矩阵 A 上各行得线性变换，则矩阵 U 的行空间与矩阵 A 的行空间一致，则 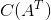 的一组基即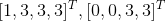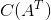为 ， 为 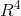 下的二维子空间。

矩阵 A 的零空间 N(A) 定义为方程组 Ax=0 的解，矩阵消元后 Ux=0 的解与 Ax=0 一致，则 Ux=0 的特解为 N(A) 的一组基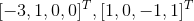，，N(A) 为  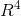下的二维子空间。

矩阵 A 的列空间 C(A) 的一组基为矩阵 A 上对应的主元列，由于 Ax=0 与 Ux=0 有相同解，则矩阵 A 中的列与矩阵 U 中的列使用相同的线性组合得到零向量，

故矩阵 U 上列的相关性也同样表现了矩阵 A 上列的相关性，但没有构成同一个列空间。矩阵 U 上主元所在列是线性不相关，则矩阵 U 上主元对应的矩阵 A 上的列也线性不相关。

C(A) 的一组基为 ，C(A) 为 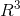 上的二维子空间。

矩阵 A 的左零空间 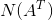 隐藏在矩阵消元过程中，EPA=U，U 中最后一行为零向量，满足 ，

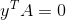则 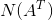 的一组基对应于 EP 矩阵 的最后一些元素 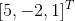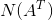， 为 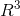 上的一维子空间。

三 求解 Ax=b

求解矩阵 ，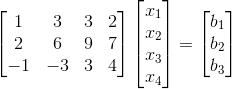

通过高斯消元得 ，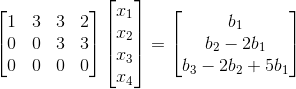

当 向量 b 满足 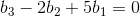 时，方程 Ax=b 有解，否则，方程无解。

任意满足 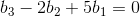 的向量 b 构成矩阵 A 的列空间，由于列空间与左零空间正交，则关系式的系数表示矩阵 A 的做了空间的基向量。

当向量 b 不满足 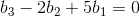 时，向量 b 不在矩阵 A 的列空间中，方程组无解。

当向量 b 满足 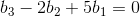 时，向量 b 在矩阵 A 的列空间中，方程组有一个或多个解，此时需要考虑矩阵 A 的秩r：

1）当矩阵 A 的秩小于 4 时，方程组存在自由变量，方程组存在许多解，其解构成 4-r 维子空间；

2）当矩阵 A 的秩等于 4 时，方程组不存在自由变量，方程组仅有一个解；当前矩阵的秩最大为3，故不可能只有一个解。

下面选择一个满足条件 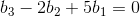 的向量 b=(1,5,5)，通过消元得到：

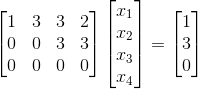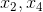， 为自由变量，解得 ，

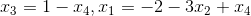将解写成向量形式为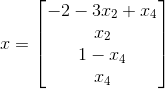：，由于 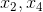 为自由变量，将其提取到出来，可整理为：

；

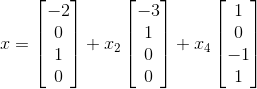可以发现 Ax=b 的解由矩阵 A 的零空间加上 Ax=b 的特解组成，其特解为设置自由变量为零求解方程组得到。以下给出方程组求解的一般流程：

1）设置  求解 Ax=0 得  ；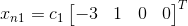

2）设置 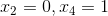 求解 Ax=0 得 ；

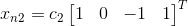3）设置 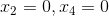 求 Ax=b 特解得 ；

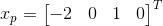4）方程组最终解为 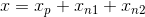，其解空间表示矩阵 A 的零空间平移  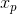所构成的超平面。

四 矩阵 A 的逆

当矩阵为方阵时，只有矩阵的秩r等于矩阵行与列时，方阵的逆存在；

当矩阵为 m*n 长方形矩阵时，当行满秩 r=m 时，矩阵列生成一个完整的 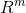空间，任意线性方程组有解求不唯一。则以下 m 个线性方程组

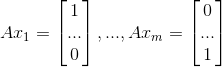均有解，其解构成了矩阵 A 的右逆 。

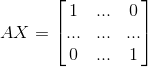由于每个方程组解不唯一，所以其右逆也不唯一，每一个右逆可求解一个方程组解。

当列满秩 r=n 时，矩阵列无法生成完整的 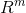 空间，只有向量 b 位于列空间时才有唯一解。然而矩阵行生成了整个  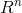空间，以下 n 个线性方程组

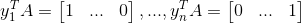均有解，其解构成了矩阵 A 的左逆 。

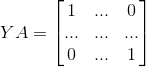以上方程组解也不唯一，所以其左逆也不唯一，所以左逆与方程组解并不一一对应。

对于长方形矩阵，如果存在行满秩或者列满秩时，可以通过以下方法构造逆矩阵：

当 r=m 时，；

当 r=n 时，。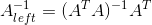

参考资料 Linear Algebra And Its Applications   Gilbert Strang