数据结构与算法（python版）

ADT抽象数据类型(ADT:Abstract Data Type):ADT是对数据进行处理的一种逻辑描述，并不涉及如何实现这些处理.

同一ADT可以采用不同的数据结构来实现：1、采用程序设计语言的控制结构和基本数据。2、类型来实现ADT所提供的逻辑接口

一、程序和算法的区别

      1、算法是对问题解决的分步描述；

      2、程序则是采用某种编程语言实现的算法，同一个算法通过不同的程序员采用不同的编程语言，能产生很多程序；

案例程序：

def sumOfN(n):
    """累计求和"""
    theSum = 0
    for i in range(1,n+1):
        theSum = theSum+i
    return theSum

 二、计算资源指标

        2.1、那么何为计算资源？

               ❖一种是算法解决问题过程中需要的存储空间或内存；（但存储空间受到问题自身数据规模的变化影响要区分哪些存储空间是问题本身描述所需，哪些是算法占用）

               ❖另一种是算法的执行时间

 

三、Python中有一个time模块，可以获取计算机系统当前时间

         3.1、算法开始前和结束后分别记录系统时间，即可得到运行时间

# 使用timeit模块对函数计时
# 创建一个timer对象，指定需要反复运行的语句
from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat %f seconds\n" % (t1.timeit(number=1000)))
t2 = Timer("test2()", "from __main__ import test2")
print("append %f seconds\n" % (t2.timeit(number=1000)))

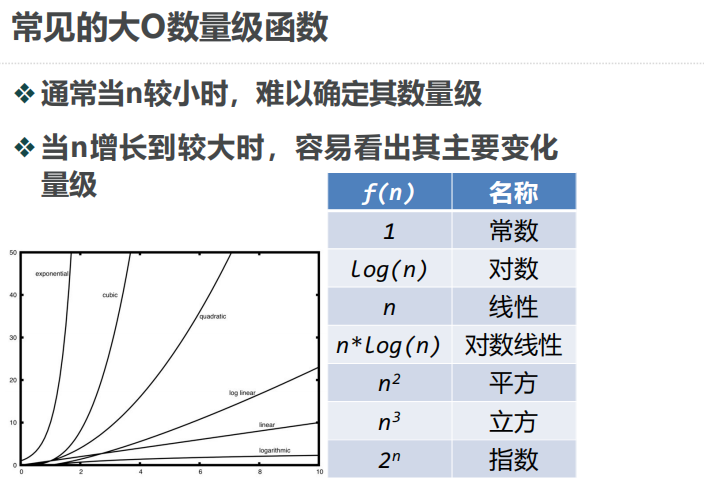
 四、数量级函数 Order of Magnitude，大O表示法

   1、基本操作数量函数T(n)的精确值并不是特别重要，重要的是T(n)中起决定性因素的主导部分用动态的眼光看，就是当问题规模增大的时候，

         T(n)中的一些部分会盖过其它部分的贡献；

   2、数量级函数描述了T(n)中随着n增加而增加速度最快的主导部分称作“大O”表示法，记作O(f(n))，其中f(n)表示T(n)中的主导部分；

                 

算法案例：“变位词”判断问题

所谓“变位词”是指两个词之间存在组成字母的
重新排列关系
如：heart和earth，python和typhon
为了简单起见，假设参与判断的两个词仅由小写
字母构成，而且长度相等
 
def anagramSolution2(s1, s2):
    """将字符串变成列表并排序，然后逐一对比"""
    alist1 = list(s1)
    alist2 = list(s2)
    alist1.sort()
    alist2.sort()
    pos = 0
    matches = True
    while pos < len(s1) and matches:
        if alist1[pos] == alist2[pos]:
            pos = pos + 1
        else:
            matches = False
    return matches

# 使用timeit模块对函数计时
# 创建一个timer对象，指定需要反复运行的语句
from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat %f seconds\n" % (t1.timeit(number=1000)))
t2 = Timer("test2()", "from __main__ import test2")
print("append %f seconds\n" % (t2.timeit(number=1000)))

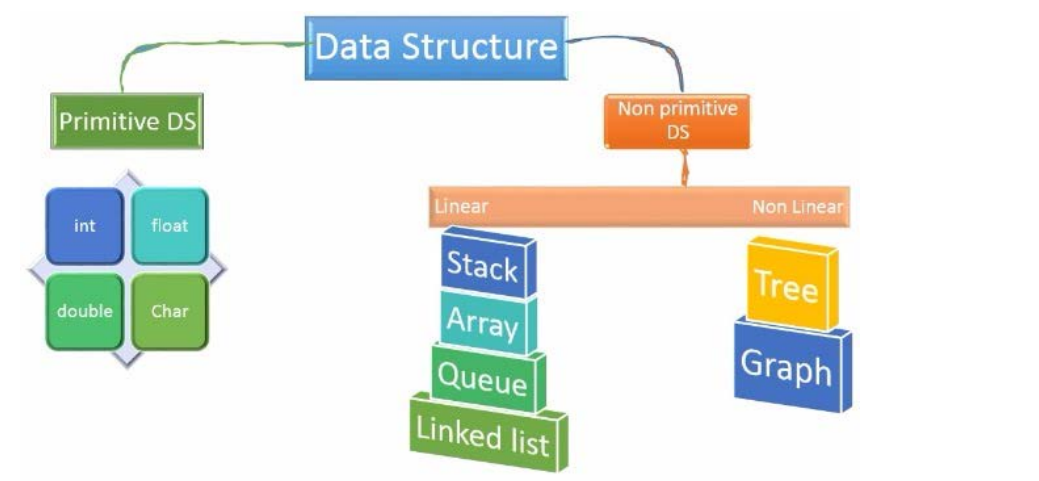
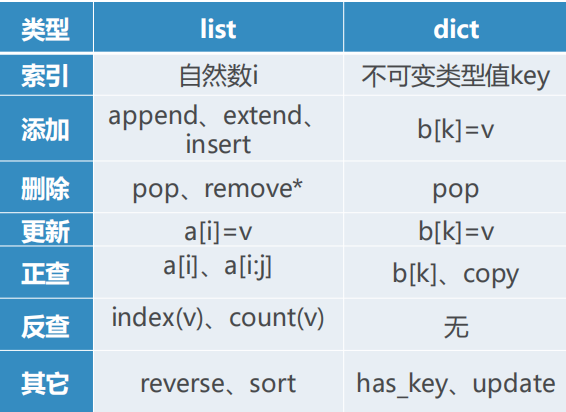
五、python数据类型-线性结构：list、dict、stack、queue、Deque、UnorderedList、OrderedList、

　　让最常用的操作性能最好，牺牲不太常用的操作：80/20准则：80%的功能其使用率只有20%

 

　　5.1、什么是线性结构Linear Structure?

        

　　5.2、栈Stack，队列Queue，双端队列Deque和列表List

　　　　这些数据集的共同点在于，数据项之间只存在先后的次序关系，都是线性结构

 

 

 

六、 栈stack：一种有次序的数据项集合，在栈中，数据项的加入和移除都仅发生在同一端，Last in First out

           这一端叫栈“顶top”，另一端叫栈“底base”，日常生活中有很多栈的应用：盘子、托盘、书堆等等

           应用场景：

           6.1、浏览器的“后退back”按钮，最先back的是最近访问的网页

      6.2、Word的“Undo”按钮，最先撤销的是最近操作

                 

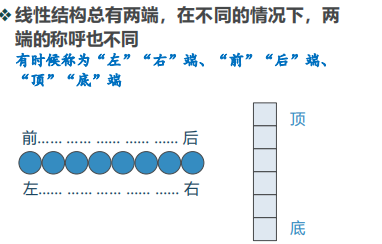
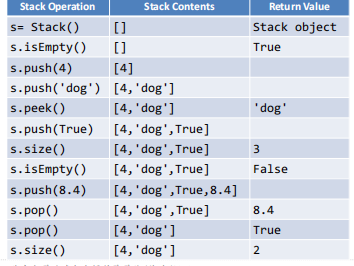
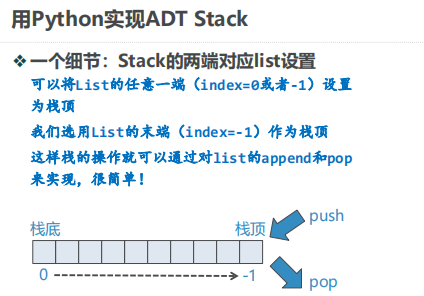
 stack的实现：

class Stack:
    """简单实现的一个栈"""
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    #这里的：不同的方法，有不同的操作
    # def push(self, item):
    #     self.items.insert(0,item)
    # def pop(self):
    #     return self.items.pop(0)
    def peek(self):
        return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)

 

 

栈的应用一：简单括号匹配（（（（（）））））

class Stack:
    """简单实现的一个栈"""
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    #这里的
    # def push(self, item):
    #     self.items.insert(0,item)
    # def pop(self):
    #     return self.items.pop(0)
    def peek(self):
        return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)

def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == "(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                s.pop()
        index = index + 1
    if balanced and s.isEmpty():
        return True
    else:
        return False

print (parChecker('((((()))))'))

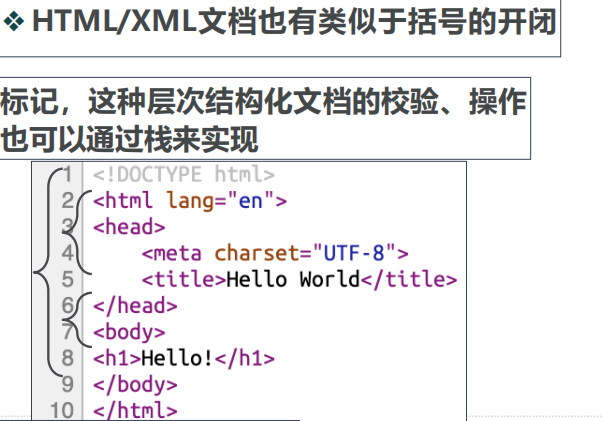
通用的写发 包含[{( 

def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]if symbol in "({[":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                top=s.pop()
                if not matches(top,symbol):
                   balanced = False
        index = index + 1
        print('s', s)
    if balanced and s.isEmpty():
        return True
    else:
        return False
def matches(open, close):
    opens = "[({"
    closers = "]})"
    return opens.index(open) == closers.index(close)

实用场景

 栈的应用二：进制之间的转化

   基本概念：二进制：二进制是计算机原理中最基本的概念，作为组成计算机最基本部件的逻辑门电路，其输入和输出
                      均仅为两种状态：0和1；

                     十进制：人类传统文化中最基本的数值概念，如果没有进制之间的转换，人们跟计算机的交互
                     会相当的困难；

所谓的“进制”，就是用多少个字符来表示整数：十进制是0～9这十个数字字符，二进制是0、1两
个字符
十进制转换为二进制，采用的是“除以2求余数”的算法

 

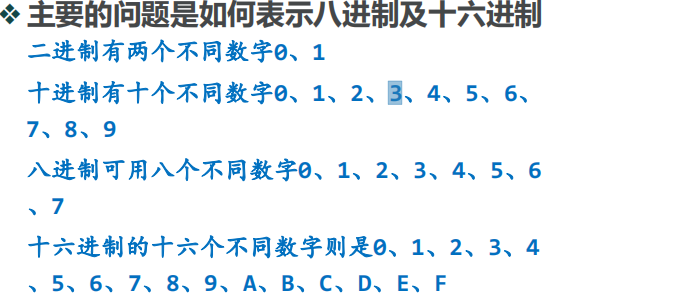
十进制转化为2进制 案例
def divideBy2(decNumber):
    remstack =Stack()
    while decNumber>0:
          rem=decNumber%2 #求余数
          remstack.push(rem)
          decNumber = decNumber//2 # 整数部分
    binString = ""
    while not remstack.isEmpty():
          binString=binString+str(remstack.pop())
    return binString
print (divideBy2(256))    

十进制转换为十六以下任意进制
def baseConverter(decNumber,base):
    digits="0123456789ABCDEF"
    remstack =Stack()
    while decNumber>0:
          rem=decNumber%base #余数
          remstack.push(rem)
          decNumber = decNumber//base # 整数部分
    newString = ""
    while not remstack.isEmpty():
          newString=newString+digits[remstack.pop()]
    return newString
print (baseConverter(256,2))

 栈的应用三：表达式应用

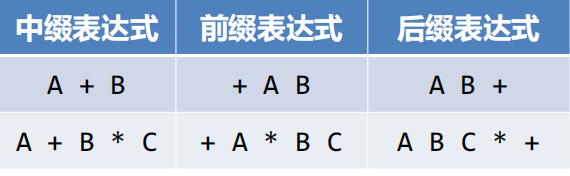
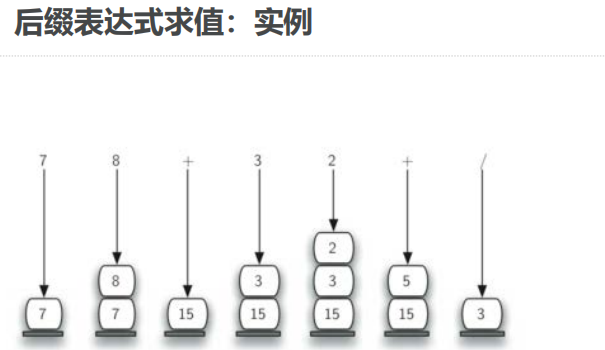
def infixToPostfix(infixexpr):
    prec = {}
    prec["*"] = 3  # 记录操作符优先级
    prec["/"] = 3
    prec["+"] = 2
    prec["-"] = 2
    prec["("] = 1
    opStack = Stack()
    postfixList = []
    tokenList = infixexpr.split()  # 解析表达式到单词列表
    for token in tokenList:
        if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
            postfixList.append(token)
        elif token == "(":
            opStack.push(token)
        elif token == ")":
            topToken = opStack.pop()
            while topToken != '(':
                postfixList.append(topToken)
                topToken = opStack.pop()
        else:  # 操作符
            while (not opStack.isEmpty()) and (prec[opStack.peek()] >= prec[token]):
                postfixList.append((opStack.pop()))
            opStack.push(token)
        while not opStack.isEmpty():
            postfixList.append(opStack.pop())  # 操作符
        return " ".join(postfixList)  # 合成后缀表达式字符串

 七：队列Queue:新加入的数据项必须在数据集末尾等待，而等待时间最长的数据项则是队首;（FIFO:First-in-first-out）先进先出

  应用场景：计算机科学中队列的例子：键盘缓冲❖键盘敲击并不马上显示在屏幕上需要有个队列性质的缓冲区，将尚未显示的敲击
                        字符暂存其中，
      特性：队列的先进先出性质则保证了字符的输入和显示次序一致性。
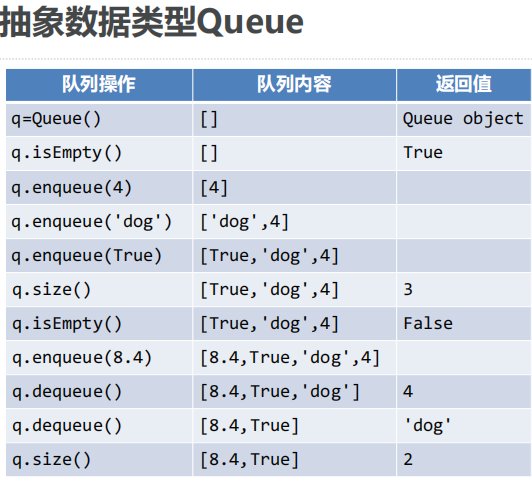
      Queue()：创建一个空队列对象，返回值为Queue对象；
      enqueue(item)：将数据项item添加到队尾，无返回值；
      dequeue()：从队首移除数据项，返回值为队首数据项，队列被修改；
      isEmpty()：测试是否空队列，返回值为布尔值
      size()：返回队列中数据项的个数。

class Queue:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def enqueue(self, item):
        # 队列首段加选项
        self.items.insert(0, item)
    def dequeue(self):
        # 队列尾端出
        return self.items.pop()
    def size(self):
        return len(self.items)

 

enqueue()复杂度为O(n)

dequeue()复杂度为O(1)

def hotPotato(namelist, num):
    simqueue = Queue()
    for name in namelist:
        simqueue.enqueue(name)
    while simqueue.size() > 1:
        for i in range(num):
            simqueue.enqueue(simqueue.dequeue())
        simqueue.dequeue()
    return simqueue.dequeue()

       

 

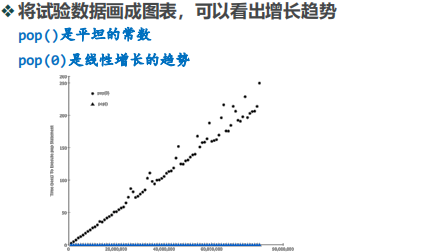
五、list：最常用的是：按索引取值和赋值（v =a[i], a[i]= v）、线性结构：【】

四种生成向list里面加数据的方式

def test1():
    l = []
    for i in range(1000):

          '循环连接列表（+）'

        l = l + [i]
 
def test2():
    l = []
    for i in range(1000):
        l.append(i)
 
def test3():
    '列表推导式'

    l = [i for i in range(1000)]
 
def test4():
    l = list(range(1000))