【leetcode】1217. Minimum Cost to Move Chips to The Same Position

We have n chips, where the position of the ith chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:

• position[i] + 2 or position[i] - 2 with cost = 0.
• position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

Example 1:

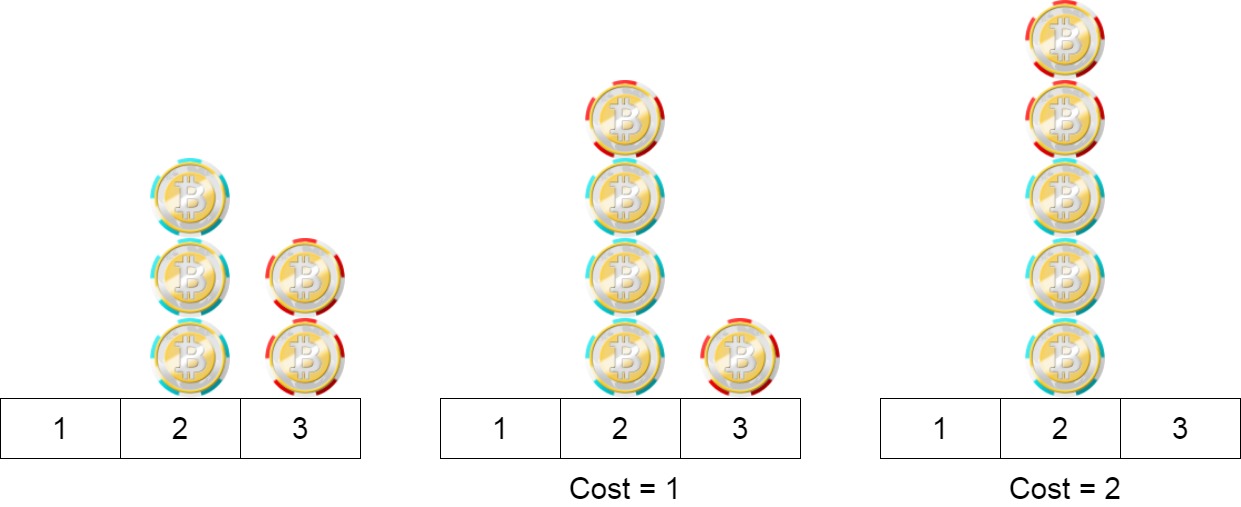
Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at position  3 to position 2. Each move has cost = 1. The total cost = 2.

Example 2:

Input: position = [1,1000000000]
Output: 1

这道题乍一看还挺复杂，但仔细想一想还是挺简单，题目的意思是将n个chips移动到一起最小的花销，而且移动的cost有规定，如果距离差一，则移动到一起cost=1，如果距离差二，则移动到一起cost=0，这句话隐含的含义是就是，如果两个chips之间距离为偶数的话，则cost=0，就可以移动到一起。如果距离是奇数的话，移动到一起cost=1。这样的话就可以将所有chips分成两组，奇数组和偶数组，然后将二者中chips个数小的往chips个数较多的移动即可，简而言之就是输出二者的最小值。

class Solution {
public:
    int minCostToMoveChips(vector<int>& position) {
       // 如果位置之间的差距是2的倍数 则可以化为一类
       // 如果位置之间的差距是奇数则 则差距为1
       // 所以可以将所有位置拆分为奇数 或者偶数
       // 奇数position 移动到1 的cost 都为0 偶数position 移动到2 的cost 都为0
        int dp[2]={0};
        for(auto pp:position){
            if(pp&1==1){
                dp[1]+=1;
            }
            else{
                dp[0]+=1;
            }
        }
        return min(dp[0],dp[1]);
    }
};