分组密码（五）AES算法② — 密码学复习（八）

在上一篇简单复习了AES的历史时间节点、产生背景、与DES的对比、算法框图（粗略）以及一些数学基础，如果不记得的话点击这里回顾。下面将介绍AES算法的细节。

下面给出AES算法的流程，图片来源：密码算法详解——AES。

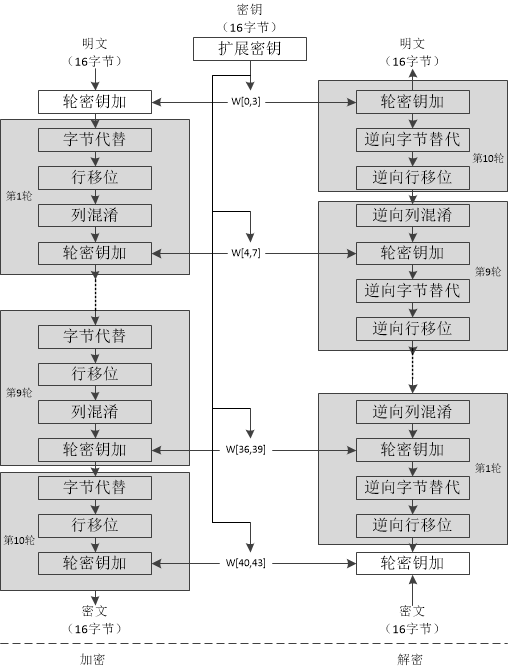
通过上图可以知道，AES的加密算法主要可以概括为：

① 一个初始轮密钥加变换

② Nr-1轮的标准轮变换

③ 最后一轮的非标准轮变换

注意：

① 第一步和最后一步都用了轮密钥加，因为没有密钥参与的变换都是容易被攻破的。

② DES的IP和IP^-1都没有密钥的参与。

8.1 轮变换 —— 加密轮函数

下面用伪代码的形式对其过程进行介绍。在AES中，除最后一轮外，其它轮次都是运行标准轮函数，最后一轮运行非标准轮函数。

① 标准轮变换

1 Round(State,RoundKey)

2 {

3     ByteSub(State);                 // S盒变换

4     ShiftRow(State);                // 行移位变换

5     MixColumn(State);               // 列混合变换

6     AddRoundKey(State,RoundKey);    // 轮密钥加变换

7 }

② 最后一轮，非标准轮函数

1 FinalRound(State,RoundKey)

2 {

3     ByteSub(State);                 // S盒变换

4     ShiftRow(State);                // 行移位变换

5     AddRoundKey(State,RoundKey);    // 轮密钥加变换

6 }

通过代码可以发现：最后一轮是没有列混合的。

8.1.1 S盒变换 ByteSub(State)

① S盒变换是AES的唯一的非线性变换，是AES安全的关键。

② AES使用16个相同的S盒，DES使用的是8个不同的S盒。

③ AES的S盒有8位输入，8位输出，是一种非线性置换；DES的S盒有6位输入，4位输出，是一种非线性压缩。

S盒变换可分为2步：（1）求逆；（2）代入公式计算。

（1）第一步：

把输入字节用其GF(2⁸)的逆来代替；

把输入字节看成GF(2⁸)上的元素；

求出其在GF(2⁸)上的逆元素；

用该逆元素代替原输入字节。

（2）第二步：

对上面的结果做如下仿射变换：

注意：

S盒变换的第一步是把字节的值用它的乘法逆来代替，是一种非线性变换。
第二步是仿射运算，是线性变换。
由于系数矩阵中每列都有5个1，说明改变输入任意一位，输出中5位发生变化。
由于系数矩阵中每行都有5个1，说明输出的每一位都与输入的5位相关。

8.1.2 行移位变换 ShiftRow(State)

① 行移位变换对状态的行进行循环移位；

② 第0行不移位，第1行移C1字节，第2行移C2字节，第3行移C3字节。

Nb	C1	C2	C3
4	1	2	3
6	1	2	3

③ 行移位属于置换，属于线性变换。本质在于把数据打乱重排，其扩散作用。

8.1.3 列混合变换 MixColumn(State)

① 列混合变换把状态的列视为GF(2⁸)上的多项式a(x)乘以一个固定的多项式c(x),并模x⁴+1.

b(x) = a(x)c(x) mod x⁴+1

其中，c(x)= 03x³+01x²+01x+02.

② 列混合变换属于线性变换，起扩散作用。

③ c(x)与x⁴+1互素，从而保证c(x)存在逆多项式d(x),而c(x)d(x)=1 mod x⁴+1，只有逆多项式存在，才能进行解密。

写成矩阵的形式：

8.1.4 轮密钥加变换 AddRoundKey(State,RoundKey)

① 把轮密钥与状态进行模2相加

② 轮密钥根据密钥产生算法产生

③ 轮密钥长度等于数据块长度

8.2 轮密钥的产生

① 加密迭代中每一轮需要一个轮密钥参与加密

② 轮密钥根据密钥产生算法通过用户密钥得到

③ 密钥产生分两步进行：

（1）密钥扩展

（2）轮密钥选择

④ 密钥扩展将用户密钥扩展为一个扩展密钥

⑤ 密钥选择从扩展密钥中选出轮密钥

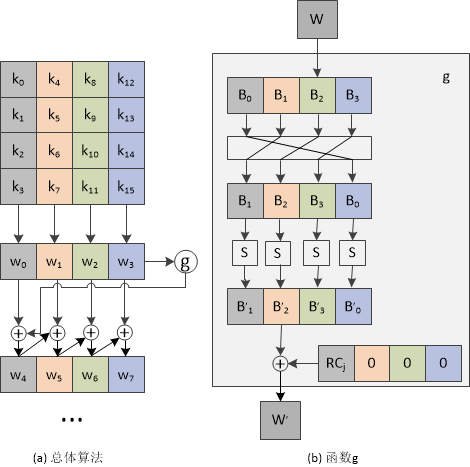
密钥扩展的原理图如下图所示，图片来源：密码算法详解——AES。

8.2.1 密钥扩展

① 密钥扩展产生扩展密钥。

② 用一个字元素的一维数组W[Nb*(Nr+1)]表示扩展密钥。

③ 用户密钥放在该数组最开始的Nk个字中。

④ 其它的字由它前面的字经过处理后得到。

⑤ 分Nk≤6和Nk＞6两种密钥扩展算法。

（1）Nk ≤ 6的密钥扩展

① 最前面的Nk个字是由用户密钥填充的

② 之后的每一个字W[j]等于前面的字W[j-1]与Nk个位置之前的字W[j-Nk]的异或

③ 而且对于Nk的整数倍的位置处的字，在异或之前，对W[j-1]进行Rotl变换和ByteSub变换，之后再异或一个常数Rcon.

当j不是Nk的整数倍：W_j=W_j-Nk⊕W_j-1

当j是Nk的整数倍：W_j=W_j-Nk⊕ByteSub(Rotl(W_j-1)⊕Rcon[j/Nk]

说明：

Rotl是一个字里的字节循环左移函数：

设 W=(A,B,C,D) 则 Rotl(W)=(B,C,D,A)

轮常数Rcon与Nk无关，且定义为：

Rcon[i] = (RC[i],'00','00','00')

RC[0] = '01'

RC[i] = xtime(RC[i-1])

（2）Nk ＞ 6的密钥扩展

说明：

Nk＞6的密钥扩展与 Nk≤6的密钥扩展基本相同，不同之处在于：如果j被Nk除的余数=4，则在异或之前，对W[j-1]进行ByteSub变换。

增加ByteSub变换是因为当Nk＞6时密钥很长，仅仅对Nk的整数倍的位置处的字进行ByteSub变换，就显得ByteSub变换的密度比较稀，安全程度不够强。

8.2.2 轮密钥的选择

根据分组大小，依次从扩展密钥中取出轮密钥。

前面的Nb个字作为轮密钥0，接下来的Nb个字作为轮密钥1...

8.3 AES的基本逆变换

AES的加密算法不是对合运算，所以解密算法和加密算法不同。

AES的巧妙之处：虽然解密算法和加密算法不同，但解密算法与加密算法的结构相同。

把加密算法的基本变换换成逆变换，便得到解密算法。

AES的基本变换都是可逆的：

① 轮密钥加的逆就是其本身：(AddRoundKey)^-1 = AddRoundKey

② 行移位变换的逆就是状态的后三行分别移位Nb-C1、Nb-C2、Nb-C3个字节。

③ 列混合的逆

状态的每列都乘以c(x)的逆多项式d(x)：

d(x) = (c(x))^-1 mod x⁴+1

c(x) = 03x³+01x²+01x+02

d(x) = 0Bx³+0Dx²+09x+0E

④ S盒变换的逆

第一步：首先进行逆仿射变换；

第二步：再把每个字节用其在GF(2⁸)上的逆来代替。

（1）把输入字节看成GF(2⁸)上的元素

（2）求出其在GF(2⁸)上的逆元素

（3）用该逆元素代替原输入字节

注：S盒的逆仿射变换：

⑤ 解密的密钥扩展

解密的密钥扩展与加密的密钥扩展不同，解密的密钥扩展定义如下：

（1）加密算法的密钥扩展

（2）把InvMixColumn（逆列混合）应用到除第一和最后一轮外的所有轮密钥上。

⑥ 逆轮变换

（1）标准拟轮变换

1  Inv_Round(State,RoundKey)

2  {

3      Inv_ByteSub(State);             // S盒变换的逆

4      Inv_ShiftRow(State);            // 逆行移位变换

5      Inv_MixColumn(State);           // 逆列混合变换

6      AddRoundKey(State,RoundKey);    // 轮密钥加变换

7  }

（2）最后一轮，非标准逆轮函数

1  Inv_FinalRound(State,RoundKey)

2  {

3      Inv_ByteSub(State);             // S盒变换的逆

4      Inv_ShiftRow(State);            // 逆行移位变换

5      AddRoundKey(State,RoundKey);    // 轮密钥加变换

6  }

8.4 AES的实现

实现方法：软件、硬件

软件方法：

① 基于算法的描述 —— 效率不够高

② 基于查表 —— 时空折换，提高效率

基于查表：

① S盒，本质上是8进8出，但要S盒和逆S盒2个表。

② 列混合变换

GF(2⁸)的非零元素构成循环群，可通过加法和查表实现乘法。逆列混合同理。

8.5 AES的安全性

能够抵抗目前所有的已知攻击。①穷举攻击 ②差分攻击 ③线性攻击 ④Square攻击 ⑤侧信道攻击

目前已有低于穷举复杂度的攻击方法，但都还不能对AES构成本质的威胁。

8.6 AES的体现

AES体现了香农的密码设计理论。

体现了公开设计的原则。

实践是检验AES密码安全性的唯一标准。

8.7 AES的优点

① 运算速度快

② 对内存的需求非常低，适合于受限环境

③ 分组长度和密钥长度设计灵活

④ AES的密钥长度比DES的密钥长度要长，用穷举法破译较难

⑤ 很好的抵抗差分密码分析和线性密码分析的能力