Coursera Deep Learning笔记 卷积神经网络基础

参考1

参考2

1. 计算机视觉

使用传统神经网络处理机器视觉的一个主要问题是输入层维度很大。例如一张64x64x3的图片，神经网络输入层的维度为12288。

如果图片尺寸较大，例如一张1000x1000x3的图片，神经网络输入层的维度将达到3百万，使得网络权重W非常庞大。

这样会造成两个后果:

• 一是神经网络结构复杂，数据量相对不够，容易出现过拟合；

• 二是所需内存、计算量较大。解决这一问题的方法就是使用卷积神经网络（CNN）。

2. 边缘检测示例

神经网络由浅层到深层，分别可以检测出图片的边缘特征 、局部特征（例如眼睛、鼻子等）、整体面部轮廓。

如何检测图片的边缘：

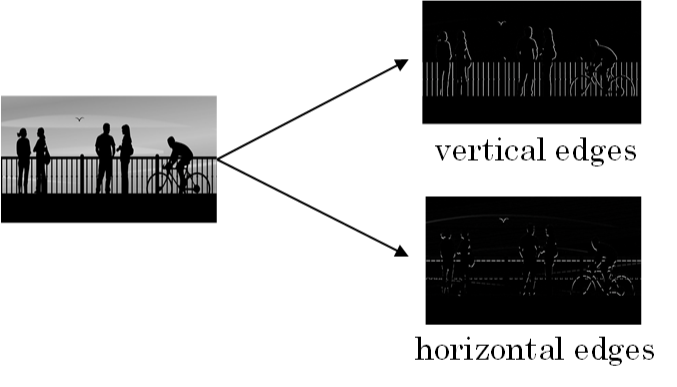
• 垂直边缘（vertical edges）

• 水平边缘（horizontal edges）

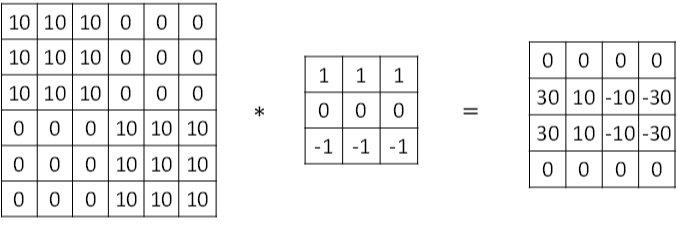
图片的边缘检测可以通过与相应滤波器进行卷积来实现。以垂直边缘检测为例，原始图片尺寸为6x6，滤波器filter尺寸为3x3，卷积后的图片尺寸为4x4，得到结果如下：

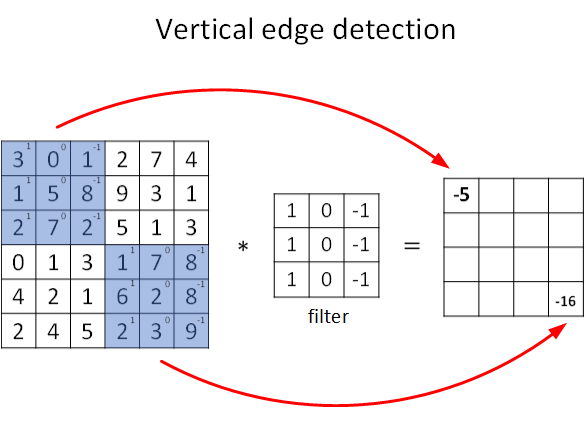
∗表示卷积操作。python中，卷积用conv_forward()表示；tensorflow中，卷积用tf.nn.conv2d()表示；keras中，卷积用Conv2D()表示。

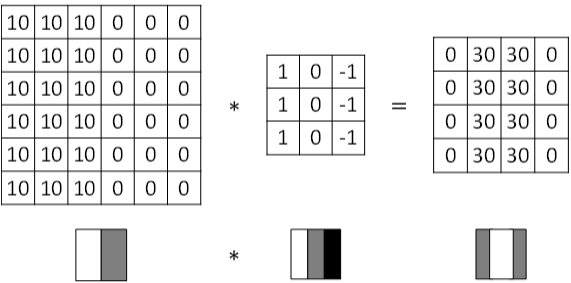
3. 更多边缘检测内容

图片边缘有两种渐变方式，一种是由明变暗，另一种是由暗变明。

以垂直边缘检测为例，下图展示了两种方式的区别。实际应用中，这两种渐变方式并不影响边缘检测结果，可以对输出图片取绝对值操作，得到同样的结果。

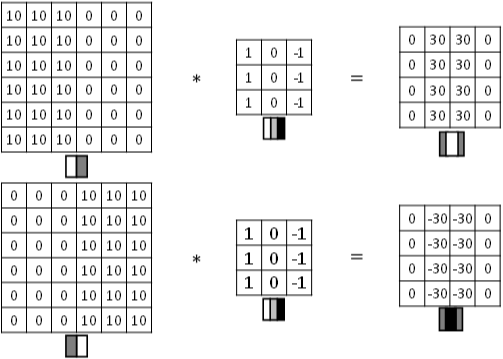
垂直边缘检测和水平边缘检测的滤波器算子如下所示：

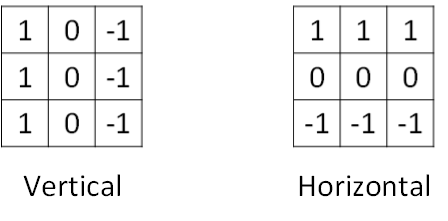
水平边缘检测:

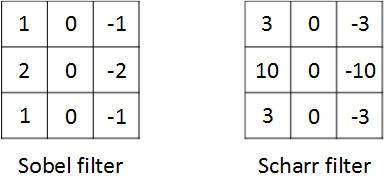
其他常用的filters，例如Sobel filter和Scharr filter。这两种滤波器的特点是：增加图片中心区域的权重。

在深度学习中，如果想检测图片的各种边缘特征，而不仅限于垂直边缘和水平边缘，那么filter的数值一般需要通过模型训练得到，类似于标准神经网络中的权重W一样由梯度下降算法反复迭代求得。

CNN的主要目的：就是计算出这些filter的数值。确定得到了这些filter后，CNN浅层网络也就实现了对图片所有边缘特征的检测。

4. Padding

如果原始图片尺寸为n x n，filter尺寸为f x f，则卷积后的图片尺寸为(n-f+1) x (n-f+1)，注意f一般为奇数。出现两个问题：

• 卷积运算后，输出图片尺寸缩小

• 原始图片边缘信息对输出贡献得少，输出图片丢失边缘信息

为了解决图片缩小的问题，可以使用padding方法，即把原始图片尺寸进行扩展，扩展区域补零，用p来表示每个方向扩展的宽度。

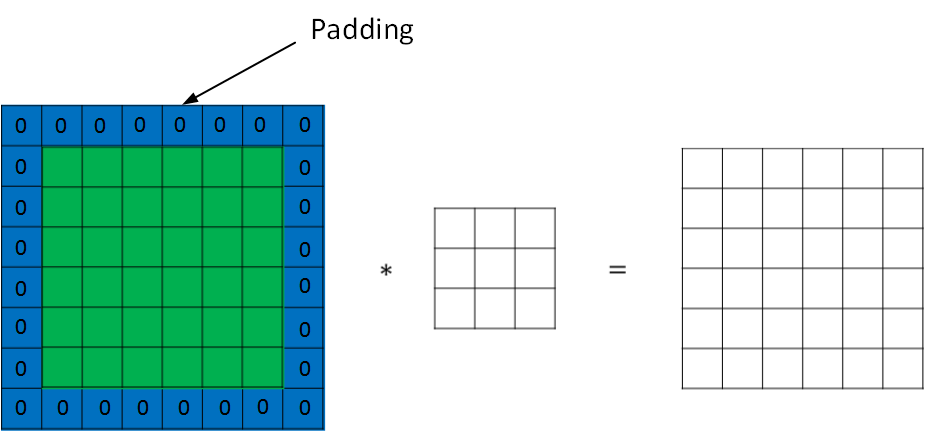
经过padding之后，原始图片尺寸为(n+2p) x (n+2p)，filter尺寸为f x f，则卷积后的图片尺寸为(n+2p-f+1) x (n+2p-f+1)。

若要保证卷积前后图片尺寸不变，则p应满足：

\[p = \frac{f-1}{2}
\]

• 没有padding操作，\(p = 0\)，称之为“Valid convolutions”；

• 有padding操作，\(p = \frac{f - 1}{2}\), 称之为 "Same convolutions"
  
  ​

  • 如果有stride为s，原尺寸为n，则推出 \(p = \frac {s \times n - n - s + f}{2}\)

5. 卷积步长(Strided Convolutions)

Stride表示filter在原图片中水平方向和垂直方向每次的步进长度。之前默认stride=1。

若stride=2，则表示filter每次步进长度为2，即隔一点移动一次。

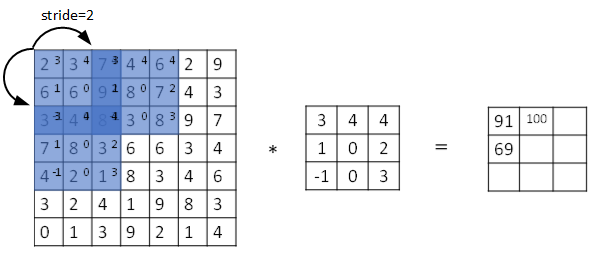
我们用s表示stride长度，p表示padding长度，如果原始图片尺寸为n x n，filter尺寸为f x f，则卷积后的图片尺寸为：

\[\lfloor {\frac{n + 2p - f}{s} + 1} \rfloor \times \lfloor {\frac{n + 2p - f}{s} + 1} \rfloor
\]

\(\lfloor ... \rfloor\) 表示向下取整.

互相关（cross-correlations）与卷积（convolutions）之间区别：

• 真正的卷积运算会先将filter绕其中心旋转180度，然后再将旋转后的filter在原始图片上进行滑动计算。filter旋转如下所示：

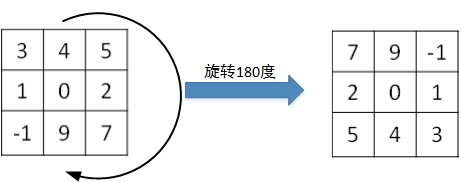
• 互相关的计算 过程则不会对filter进行旋转，而是直接在原始图片上进行滑动计算。

注意：

• 目前为止我们介绍的CNN卷积实际上计算的是互相关，而不是数学意义上的卷积。
• 为了简化计算，一般把CNN中的这种“互相关”就称作卷积运算。因为 滤波器算子 一般是水平或垂直对称的，180度旋转影响不大
• 而且最终 滤波器算子 需要通过CNN网络梯度下降算法计算得到，旋转部分可以看作是包含在CNN模型算法中。
• 总的来说，忽略旋转运算可以大大提高CNN网络运算速度，而且不影响模型性能。
• 卷积运算遵从结合律：

\[(A * B) * C = A * (B * C)
\]

6. 卷积为何有效(Convolutions Over Volume)

对于3通道的RGB图片，其对应的滤波器算子同样也是3通道的。例如一个图片是6 x 6 x 3，分别表示图片的高度（height）、宽度（weight）和通道（#channel）。

3通道图片的卷积运算与单通道图片的卷积运算基本一致。

• 过程是将每个单通道（R，G，B）与对应的filter进行卷积运算求和，然后再将3通道的和相加，得到输出图片的一个像素值。

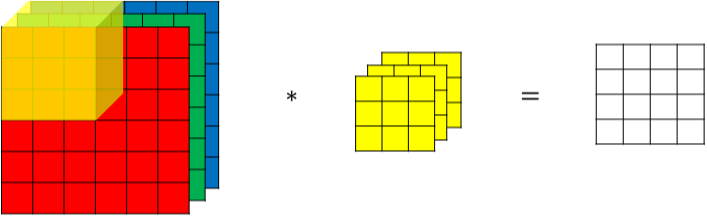
不同通道的滤波算子可以不相同

• 例如R通道filter实现垂直边缘检测，G和B通道不进行边缘检测，全部置零，或者将R，G，B三通道filter全部设置为水平边缘检测。

---

为了进行多个卷积运算，实现更多边缘检测，可以增加更多的滤波器组。

• 例如设置第一个滤波器组实现垂直边缘检测，第二个滤波器组实现水平边缘检测。这样，不同滤波器组卷积得到不同的输出，个数由滤波器组决定。

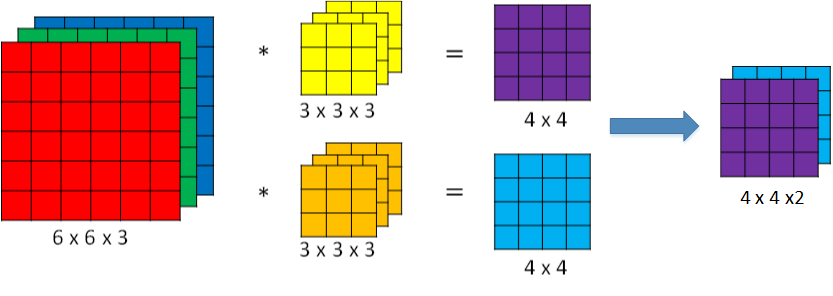
若输入图片的尺寸为 \(n \times n \times n_c\)，filter尺寸为 \(f \times f \times n_c\)，则卷积后图片尺寸为 \((n-f+1) \times (n-f+1) \times n_c{'}\)。其中：

• \(n_c\)：图片通道数目

• \(n_c{'}\)：为滤波器组个数

7. 单层卷积网络(One Layer of a Convolutional Network)

卷积神经网络的单层结构：

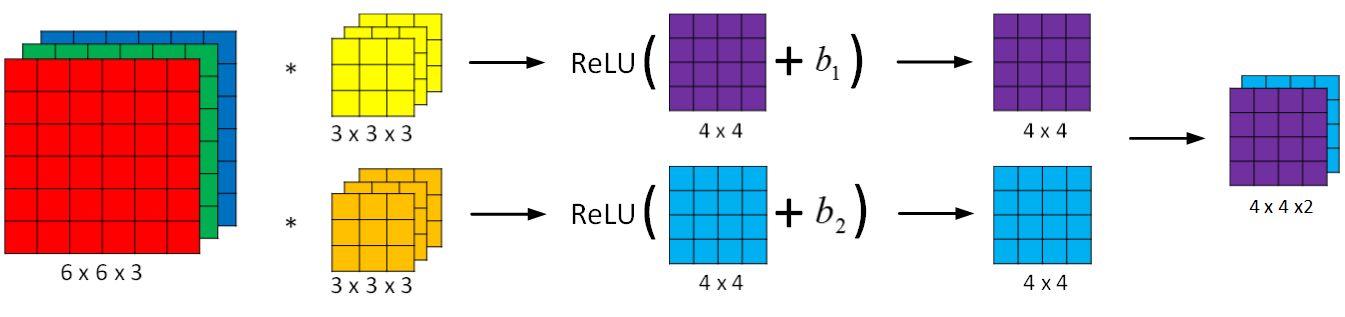
相比之前的卷积过程，CNN的单层结构多了激活函数ReLU和偏移量b。整个过程与标准的神经网络单层结构非常类似：

\[Z^{[l]} = W^{[l]}A^{[l-1]} + b \\
A^{[l]} = g^{[l]}(Z^{[l]})
\]

卷积运算对应着上式中的乘积运算，滤波器组数值对应着权重\(W^{[l]}\)，激活函数为ReLU。

计算上图中参数的数目：

• 每个滤波器组有 \(3 \times 3 \times 3 = 27\) 个参数，还有 1个偏移量b，则每个滤波器组有 27 + 1 = 28个参数，两个滤波器总共 28*2 = 56个参数

• 选定滤波器后，参数数目与输入图片尺寸无关。 例如一张1000x1000x3的图片，标准神经网络输入层的维度将达到3百万，而在CNN中，参数数目只由滤波器组决定，数目相对来说要少得多，这是CNN的优势之一。

总结，CNN单层结构的所有标记符号，设层数为 \(l\)：

• \(f^{[l]} = filter size\)

• \(p^{[l]} = padding\)

• \(s^{[l]} = stride\)

• \(n_c^{[l]} = number　of　filters\)

• \(输入维度为： n_H^{[l-1]} \times n_W^{[l-1]} \times n_c^{[l-1]}\)

• \(每个滤波器组维度： f^{[l]} \times f^{[l]} \times n_c^{[l-1]}\)

• \(权重维度： f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}\)

• \(偏置维度： 1 \times 1 \times 1 \times n_c^{[l]}\)

• \(输出维度： n_H^{[l]} \times n_H^{[l]} \times n_c^{[l]}\)

其中，

\[n_H^{[l]} = \lfloor {\frac{n_H^{[l-1]} + 2P^{[l]} - f^{[l]}}{s^{[l]}} + 1} \rfloor \\
n_W^{[l]} = \lfloor {\frac{n_W^{[l-1]} + 2P^{[l]} - f^{[l]}}{s^{[l]}} + 1} \rfloor
\]

如果有 m 个样本，进行向量化运算，相应的输出维度为：\(m \times n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}\)

8. 简单卷积层网络示例

一个简单的CNN模型：

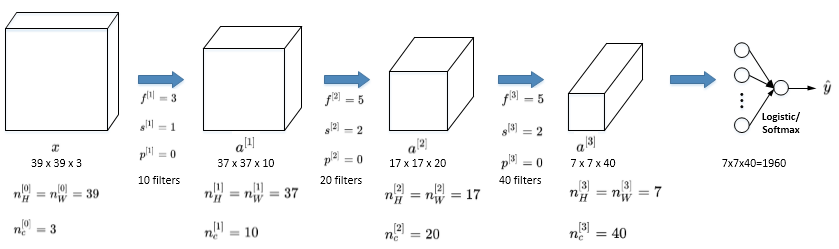
注：\(a^{[3]}\) 的维度是 7x7x40，将 \(a^{[3]}\) 排列成1列，维度1960x1，然后连接最后一级输出层。

CNN有三种类型的layer：

• Convolution层（CONV）（卷积层）

• Pooling层（POOL）（池化层）

• Fully connected层（FC）（flatten层）

9. 池化层(Pooling Layers)

Pooling layers是CNN中用来减小尺寸，提高运算速度的，同样能减小noise影响，让各特征更具有健壮性。

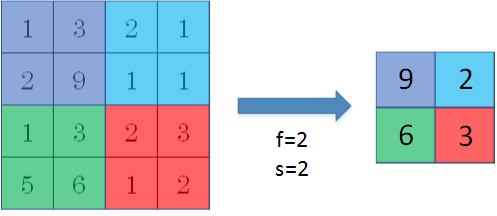
Max pooling的好处是只保留区域内的最大值（特征），忽略其它值，降低noise影响

• max pooling需要的超参数仅为 滤波器尺寸f 和 滤波器步进长度s

• 没有其他参数需要模型训练得到，计算量很小

MaxPooling：取滑动窗口里最大的值

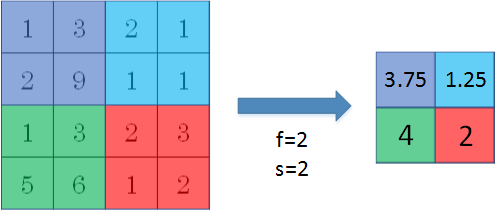
AveragePooling：取滑动窗口内所有值的平均值

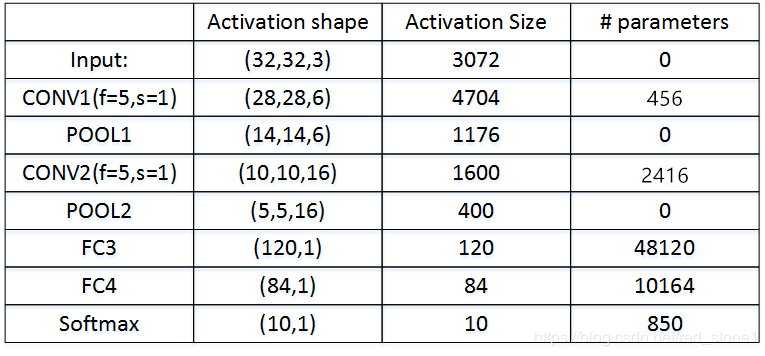
10. 卷积神经网络示例

CNN实例：

• 如图，CONV层后面紧接一个POOL层，CONV1和POOL1构成第一层，CONV2和POOL2构成第二层。

• 特别注意的是FC3和FC4为 全连接层FC，它跟标准的神经网络结构一致。

• 最后的输出层（softmax）由10个神经元构成。

整个网络各层尺寸和参数：

11. 为什么使用卷积

• 参数共享：

  • 一个特征检测器（例如垂直边缘检测）对图片某块区域有用，同时也可能作用在图片其它区域。

  • 连接的稀疏性：因为滤波器算子尺寸限制，每一层的每个输出只与输入部分区域内有关。

• CNN参数数目较小，所需的训练样本就相对较少，从而一定程度上不容易发生过拟合现象。

• CNN比较擅长捕捉区域位置偏移。也就是说CNN进行物体检测时，不太受物体所处图片位置的影响，增加检测的准确性和系统的健壮性。