数据特征分析：3.统计分析 & 帕累托分析

1.统计分析

统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析

集中趋势度量 / 离中趋势度量

One.集中趋势度量

 指一组数据向某一中心靠拢的倾向，核心在于寻找数据的代表值或中心值 —— 统计平均数
 算数平均数、位置平均数（加权平均值）

（1）算术平均数 、加权算术平均数 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline

# 1、集中趋势度量 （1）算数平均数
data = pd.DataFrame({'value':np.random.randint(100,120,100),
                    'f':np.random.rand(100)})
data['f'] = data['f'] / data['f'].sum()  # f为权重，这里将f列设置成总和为1的权重占比
print(data.head())
print('------')
# 创建数据

mean = data['value'].mean()
print('简单平均数%.2f'% mean)  # 简单算数平均值 = 总和 / 样本数量 （不涉及权重）
mean_w = (data['value'] * data['f']).sum() / data['f'].sum()
print('加权平均数%.2f'% mean_w)
# 加权算数平均值 = (x1f1 + x2f2 + ... + xnfn) / (f1 + f2 + ... + fn)

（2）位置平均数

data['value'].plot(kind = 'kde',style = '--k',grid = True) 密度曲线；  plt.axvline()

# 1、集中趋势度量  （2）位置平均数

m = data['value'].mode().tolist() #变成一个列表，可能不止一个
print('众数为',m) # 众数是一组数据中出现次数最多的数，这里可能返回多个值

med = data['value'].median()
print('中位数为%i'% med)  # 中位数指将总体各单位标志按照大小顺序排列后，中间位置的数字
mean = data['value'].mean()
print('简单平均数%.2f'% mean) #中位数和平均数差不多  

data['value'].plot(kind = 'kde',style = '--k',grid = True)
# 密度曲线

plt.axvline(mean,hold=None,color='r',linestyle="--",alpha=0.8)
plt.text(mean + 5,0.005,'简单算数平均值为：%.2f' % mean, color = 'r')
# 简单算数平均值

plt.axvline(mean_w,hold=None,color='b',linestyle="--",alpha=0.8)
plt.text(mean + 5,0.01,'加权算数平均值：%.2f' % mean_w, color = 'b')
# 加权算数平均值

plt.axvline(med,hold=None,color='g',linestyle="--",alpha=0.8)
plt.text(mean + 5,0.015,'中位数：%i' % med, color = 'g')
# 中位数
# **这里三个数text显示的横坐标一致，目的是图示效果不拥挤

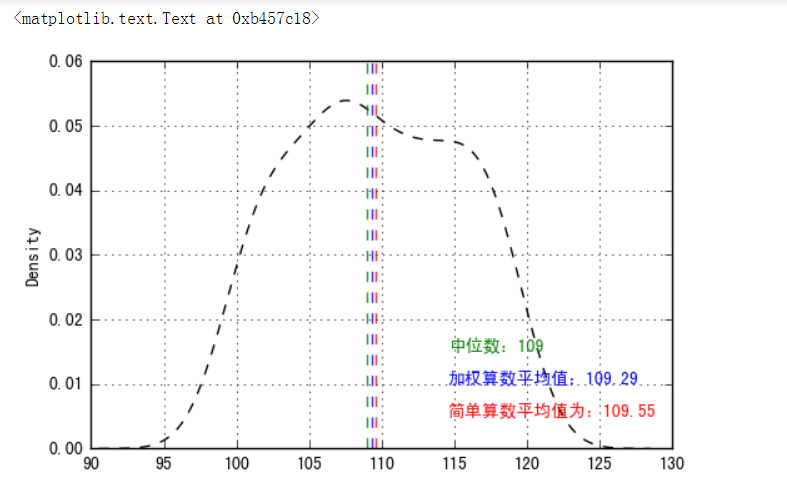
密度曲线，100-150的密度分布，绿色的为中位数，红色的为简单的算术平均值，蓝色的为加权平均值。

Two.离中趋势度量

 指一组数据中各数据以不同程度的距离偏离中心的趋势
 极差与分位差、方差与标准差、离散系数 
（1）极差、分位差 

data.plot.box(vert=False, grid=True, color=color, figsize=(10, 3)) #箱型图  

# 2、离中趋势度量
data = pd.DataFrame({'A_sale':np.random.rand(30)*1000,
                    'B_sale':np.random.rand(30)*1000},
                   index = pd.period_range('',''))
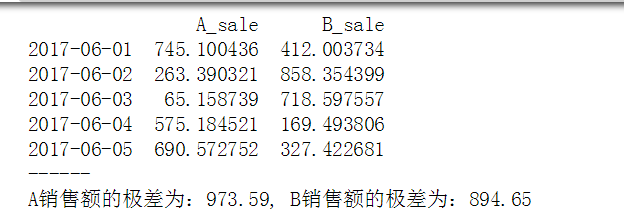
print(data.head())
print('------')
# 创建数据
# A/B销售额量级在同一水平

# （1）极差、分位差
a_r = data['A_sale'].max() - data['A_sale'].min()
b_r = data['B_sale'].max() - data['B_sale'].min()
print('A销售额的极差为：%.2f, B销售额的极差为：%.2f' % (a_r,b_r))
print('------')
# 极差
# 没有考虑中间变量的变动，测定离中趋势不稳定

sta = data['A_sale'].describe()
stb = data['B_sale'].describe()
print(sta)
print('---------')
a_iqr = sta.loc['75%'] - sta.loc['25%']
b_iqr = stb.loc['75%'] - stb.loc['25%']
print('A销售额的分位差为：%.2f, B销售额的分位差为：%.2f' % (a_iqr,b_iqr))
print('------')
# 分位差

color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')
data.plot.box(vert=False, grid=True, color=color, figsize=(10, 3)) #箱型图  

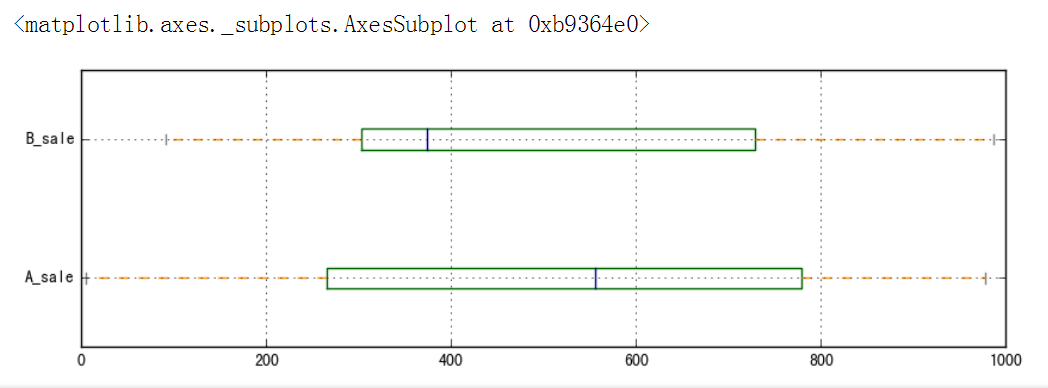
极差只能反映值的区间，不能反映里边内部的波动情况，极差越小离中趋势越小。

（2）方差与标准差

# 2、离中趋势度量
# （2）方差与标准差

a_std = sta.loc['std'] #标准差直接做个平方
b_std = stb.loc['std']
a_var = data['A_sale'].var() #方差就用到了.var()  标准差.describe()
b_var = data['B_sale'].var()
print('A销售额的标准差为：%.2f, B销售额的标准差为：%.2f' % (a_std,b_std))
print('A销售额的方差为：%.2f, B销售额的方差为：%.2f' % (a_var,b_var))
# 方差 → 各组中数值与算数平均数离差平方的算术平均数
# 标准差 → 方差的平方根
# 标准差是最常用的离中趋势指标 → 标准差越大，离中趋势越明显 

data['A_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'A密度曲线')
中位数-标准差 、 中文书+标准差

fig = plt.figure(figsize = (12,4))
ax1 = fig.add_subplot(1,2,1)
data['A_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'A密度曲线')
plt.axvline(sta.loc['50%'],hold=None,color='r',linestyle="--",alpha=0.8)
plt.axvline(sta.loc['50%'] - a_std,hold=None,color='b',linestyle="--",alpha=0.8)  #一个中位数-标准差
plt.axvline(sta.loc['50%'] + a_std,hold=None,color='b',linestyle="--",alpha=0.8)  #一个中位数+标准差
# A密度曲线，1个标准差

ax2 = fig.add_subplot(1,2,2)
data['B_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'B密度曲线')
plt.axvline(stb.loc['50%'],hold=None,color='r',linestyle="--",alpha=0.8)
plt.axvline(stb.loc['50%'] - b_std,hold=None,color='b',linestyle="--",alpha=0.8)
plt.axvline(stb.loc['50%'] + b_std,hold=None,color='b',linestyle="--",alpha=0.8)
# B密度曲线，1个标准差

它们的中位数是差不多的，A的两个标准差之间的距离是 小于 B曲线两个标准差之间的长度的，A相当于B来说更集中。

总结：

对于集中度和离中度就用到这几个指标，对于集中度看中间那个数值的（包括均值、算术平均值、位置平均数 ）；离中趋势看极差、标准差、方差。

2. 帕累托分析

帕累托分析（贡献度分析） → 帕累托法则：20/80定律

“原因和结果、投入和产出、努力和报酬之间本来存在着无法解释的不平衡。一般来说，投入和努力可以分为两种不同的类型：
多数，它们只能造成少许的影响；少数，它们造成主要的、重大的影响。”
→ 一个公司，80%利润来自于20%的畅销产品，而其他80%的产品只产生了20%的利润

例如：
** 世界上大约80％的资源是由世界上15％的人口所耗尽的
** 世界财富的80％为25％的人所拥有；在一个国家的医疗体系中
** 20％的人口与20％的疾病，会消耗80％的医疗资源。

一个思路：通过二八原则，去寻找关键的那20%决定性因素！

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline

data = pd.Series(np.random.randn(10)*1200 + 3000,
                                   index = list('ABCDEFGHIJ')) #10个产品的销售额
data.sort_values(ascending = False, inplace = True) #从大到小排序
data

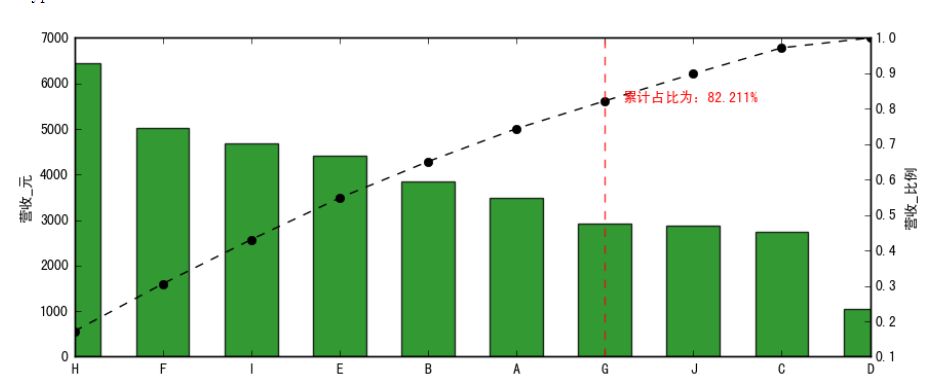
plt.figure(figsize = (10, 4))
data.plot(kind = 'bar', color = 'g', alpha = 0.8, width = 0.6)#做一个柱状图
plt.ylabel('营收_元')
# 创建营收柱状图

p = data.cumsum()/data.sum() #累计占比，除个总和;大于0.8的在C产品
key = p[p>0.8].index[0] #p[p>0.8].index -->Index(['J', 'G', 'B'], dtype='object')
key_num = data.index.tolist().index(key)  #找到对应的索引序号
print('超过80%累计占比的节点值索引为：' ,key)
print('超过80%累计占比的节点值索引位置为：' ,key_num)
print('------')
# 找到累计占比超过80%时候的index
# 找到key所对应的索引位置

p.plot(style = '--ko', secondary_y=True)#累计占比曲折线图，累计占比；# secondary_y → y副坐标轴,用次坐标轴
plt.axvline(key_num, hold = None, color = 'r', linestyle = '--', alpha = 0.8)#把80%占比那个参考线画出来，直接是key_num，因为它是X轴的索引值
plt.text(key_num+0.2,p[key],'累计占比为：%.3f%%' % (p[key]*100), color = 'r')  # 累计占比超过80%的节点
plt.ylabel('营收_比例')
# 绘制营收累计占比曲线

key_product = data.loc[:key]
print('核心产品为：')
print(key_product)
# 输出决定性因素产品