[USACO18JAN]Sprinklers

[USACO18JAN]Sprinklers

一个矩形要符合什么条件

右上角的右上有点，左下角的左下有点

所以每列的选择高度为一个区间，小于后缀最大值大于前缀最小值（不管是作为右上角还是左下角）

然后对于一个：

求完全在这个区域里的矩形个数

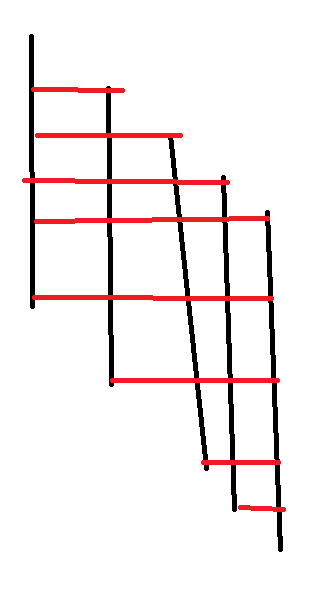
从上往下考虑，处理左下角在这一行，右上角在上面的方案数

发现每行的点对于之后的贡献分别是0+1+2+3。。。

全局变量tot维护决策点个数

删除的时候注意删除对应决策点即可。

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

namespace Miracle{
const int N=1e5+;
const int mod=1e9+;
int n;
int u[N],d[N];
ll a[N],sum[N];
int h[N];
vector<int>dele[N];
int main(){
    rd(n);
    int x,y;
    for(reg i=;i<=n;++i){
        rd(x);rd(y);
        ++x;++y;h[x]=y;
    }
    int mx=;
    for(reg i=n;i>=;--i){
        mx=max(mx,h[i]);
        u[i]=mx;
    }
    int mi=n+;
    for(reg i=;i<=n;++i){
        mi=min(mi,h[i]);
        d[i]=mi;dele[d[i]-].push_back(i);
    }
    for(reg i=;i<=n;++i){
        ++a[d[i]];--a[u[i]+];
    }
    for(reg i=;i<=n;++i){
        a[i]+=a[i-];
    }
    for(reg i=n;i>=;--i){
        sum[i]=sum[i+]+a[i];
    }
    ll ans=,tot=;
    ll len=;
    for(reg i=n;i>=;--i){
        for(reg j=;j<(int)dele[i].size();++j){
            int now=dele[i][j];
            len+=u[now]-d[now]+;
            tot-=sum[i+]-len;
        }
        ans=(ans+tot)%mod;
        tot=tot+(a[i]-)*a[i]/;
    }
    cout<<ans;
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/4/13 19:58:12
*/