吴恩达机器学习笔记35-诊断偏差和方差(Diagnosing Bias vs. Variance)
当你运行一个学习算法时,如果这个算法的表现不理想,那么多半是出现两种情况:
要么是偏差比较大,要么是方差比较大。换句话说,出现的情况要么是欠拟合,要么是过拟
合问题。那么这两种情况,哪个和偏差有关,哪个和方差有关,或者是不是和两个都有关?
搞清楚这一点非常重要,因为能判断出现的情况是这两种情况中的哪一种。其实是一个很有
效的指示器,指引着可以改进算法的最有效的方法和途径,高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题。
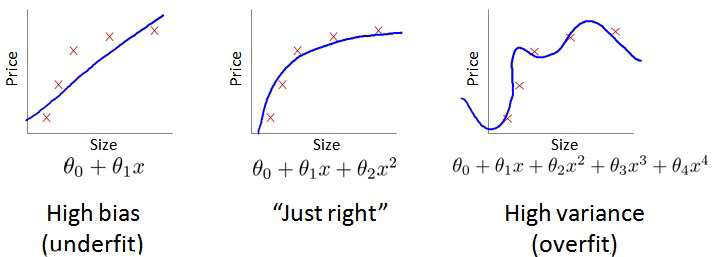
我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张
图表上来帮助分析:
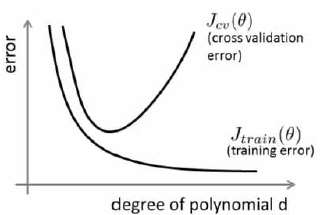
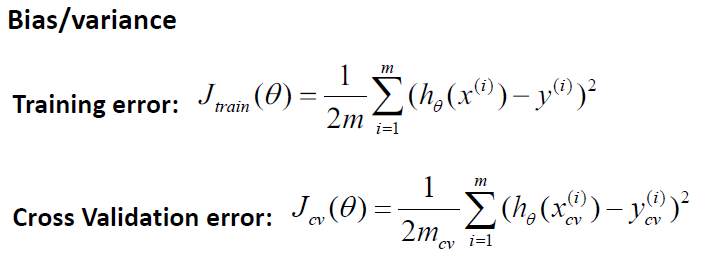

对于训练集,当
吴恩达机器学习笔记35-诊断偏差和方差(Diagnosing Bias vs. Variance)的更多相关文章
- 吴恩达机器学习笔记38-决策下一步做什么(Deciding What to Do Next Revisited)
我们已经讨论了模型选择问题,偏差和方差的问题.那么这些诊断法则怎样帮助我们判断,哪些方法可能有助于改进学习算法的效果,而哪些可能是徒劳的呢? 让我们再次回到最开始的例子,在那里寻找答案,这就是我们之前 ...
- 吴恩达机器学习笔记(六) —— 支持向量机SVM
主要内容: 一.损失函数 二.决策边界 三.Kernel 四.使用SVM (有关SVM数学解释:机器学习笔记(八)震惊!支持向量机(SVM)居然是这种机) 一.损失函数 二.决策边界 对于: 当C非常 ...
- 吴恩达机器学习笔记36-正则化和偏差/方差(Regularization and Bias_Variance)
在我们在训练模型的过程中,一般会使用一些正则化方法来防止过拟合.但是我们可能会正则化的程度太高或太小了,即我们在选择λ 的值时也需要思考与刚才选择多项式模型次数类似的问题. 我们选择一系列的想要测试的
- [吴恩达机器学习笔记]12支持向量机5SVM参数细节
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.5 SVM参数细节 标记点选取 标记点(landma ...
- [吴恩达机器学习笔记]12支持向量机2 SVM的正则化参数和决策间距
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.2 大间距的直观理解- Large Margin I ...
- [吴恩达机器学习笔记]11机器学习系统设计3-4/查全率/查准率/F1分数
11. 机器学习系统的设计 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 11.3 偏斜类的误差度量 Error Metr ...
- Coursera-AndrewNg(吴恩达)机器学习笔记——第三周
一.逻辑回归问题(分类问题) 生活中存在着许多分类问题,如判断邮件是否为垃圾邮件:判断肿瘤是恶性还是良性等.机器学习中逻辑回归便是解决分类问题的一种方法.二分类:通常表示为yϵ{0,1},0:&quo ...
- Coursera-AndrewNg(吴恩达)机器学习笔记——第一周
一.初识机器学习 何为机器学习?A computer program is said to learn from experience E with respect to some task T an ...
- [吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.3 大间距分类背后的数学原理- Mathematic ...
随机推荐
- mysql学习记录
干净卸载mysql:https://blog.csdn.net/cxy_summer/article/details/70142322mysql 解压缩版安装说明:https://jingyan.ba ...
- scrapy 爬取智联招聘
准备工作 1. scrapy startproject Jobs 2. cd Jobs 3. scrapy genspider ZhaopinSpider www.zhaopin.com 4. scr ...
- 内嵌圆角CSS实现
前言 开发项目时,经常会遇到如上图左上角和右上角这种内嵌的圆角效果,在以前css3还没有普及时不用说一张图片搞定,但是到现在我们完全可以用css去实现. 实现 第一步:思路 仔细观察这个小缺角,它其实 ...
- openstack 王者归来学习笔记
rpc.call方法执行的流程:(下次看代码的时候可以根据这流程来看,注意:由于rpc服务器和客户端具有很松的耦合性,因此以上步骤并不是绝对的.) 1.rpc服务器定义和启动rpc服务 2.rpc服务 ...
- testXSS <img src="aa" onerror="javascript:alert('XSS');"/>
adsa </p><img src="aa" onerror="javascript:alert('XSS');"/><p> ...
- oracle primary key & foreign key
主键:一个表中只有一个主键约束,但是一个主键约束可以由数据表中的多个列组成:primary key alter table TName add constraints pk_name PRIMARY ...
- linux '--stdin'错误 -批量修改密码
虚拟机:VMware虚拟机 系统:Linux ubuntu 4.4.0-31-generic #50~14.04.1-Ubuntu SMP Wed Jul 13 01:07:32 UTC 2016 ...
- sql中varchar(n),nvarchar(n) 长度性能及所占空间分析
sql中varchar(n),nvarchar(n) 长度性能及所占空间分析 1.varchar(n),nvarchar(n) 中的n怎么解释: nvarchar(n)最多能存n个字符,不区分中英文. ...
- Js2WordCloud 词云用法
1.引入 npm 安装: npm install js2wordcloud --save 通过script引入: <script src="dist/js2wordcloud.min. ...
- STL之vector容器详解
vector 容器 vector是C++标准模版库(STL,Standard Template Library)中的部分内容.之所以认为是一个容器,是因为它能够像容器一样存放各种类型的对象,简单的说: ...
