数据结构图解（递归，二分，AVL，红黑树，伸展树，哈希表，字典树，B树，B+树）

递归反转

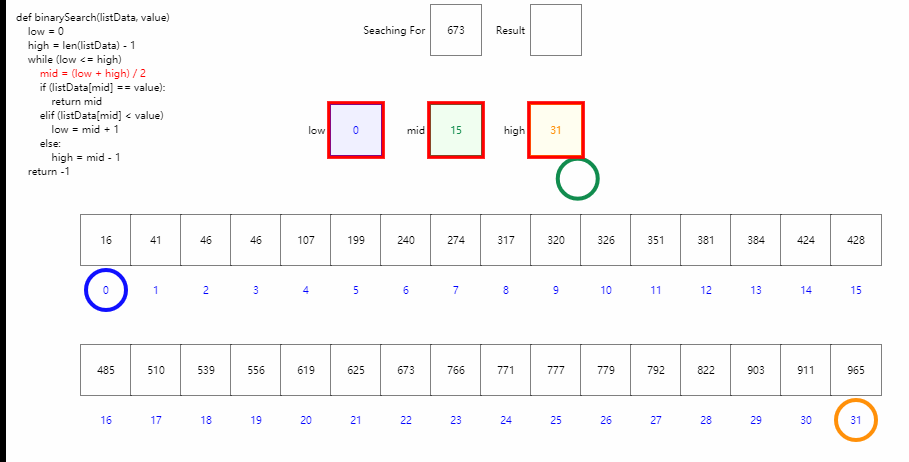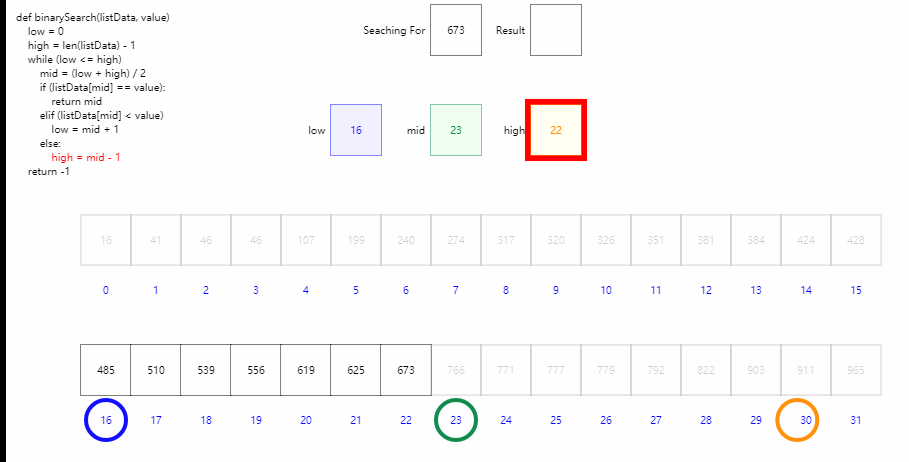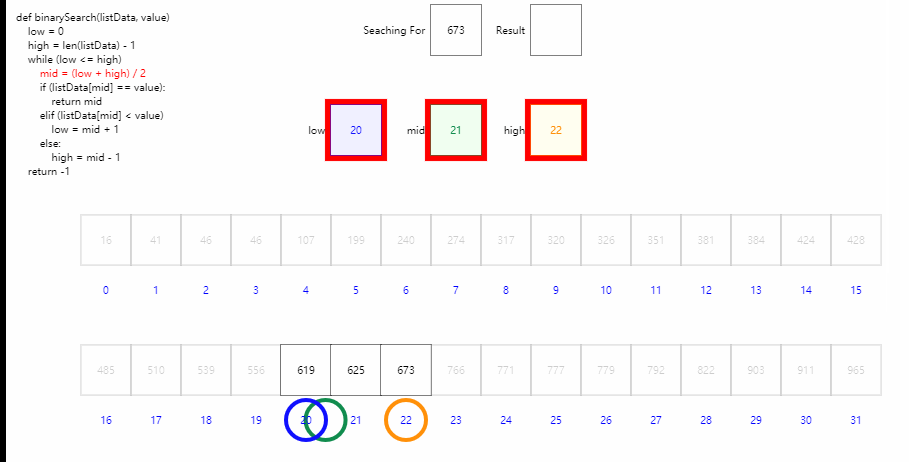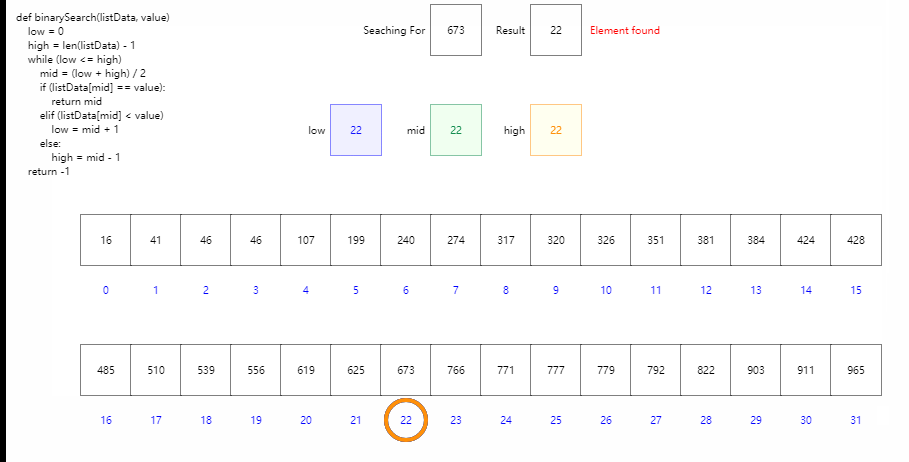
二分查找

AVL树

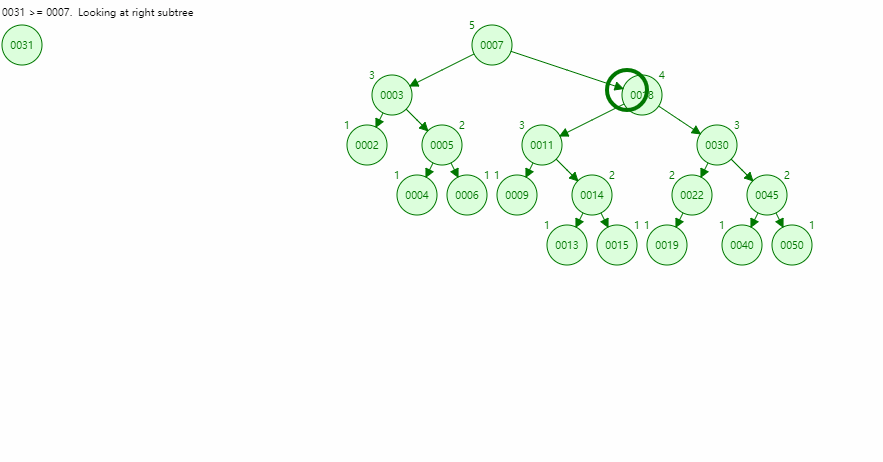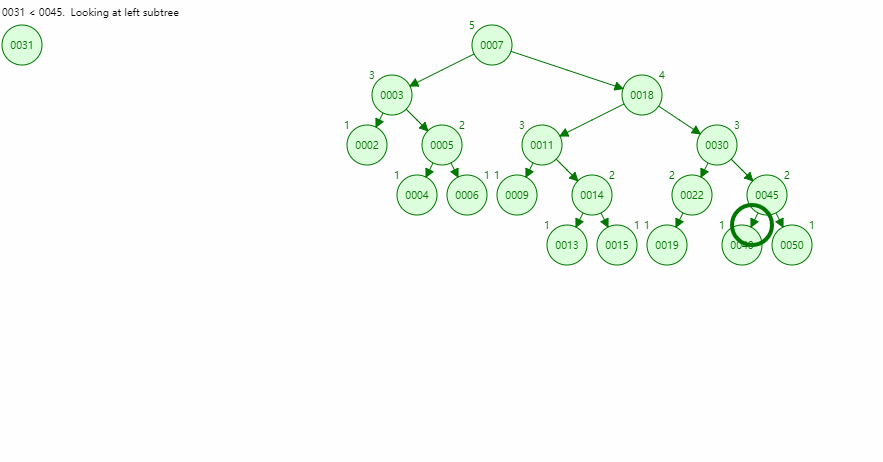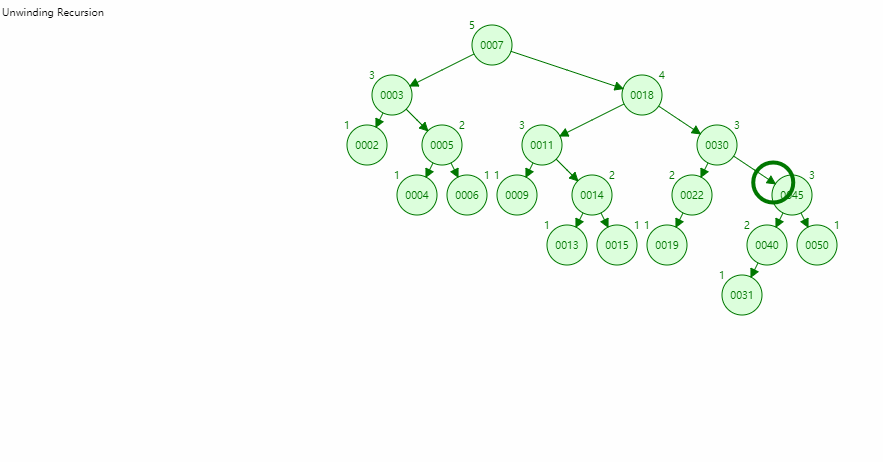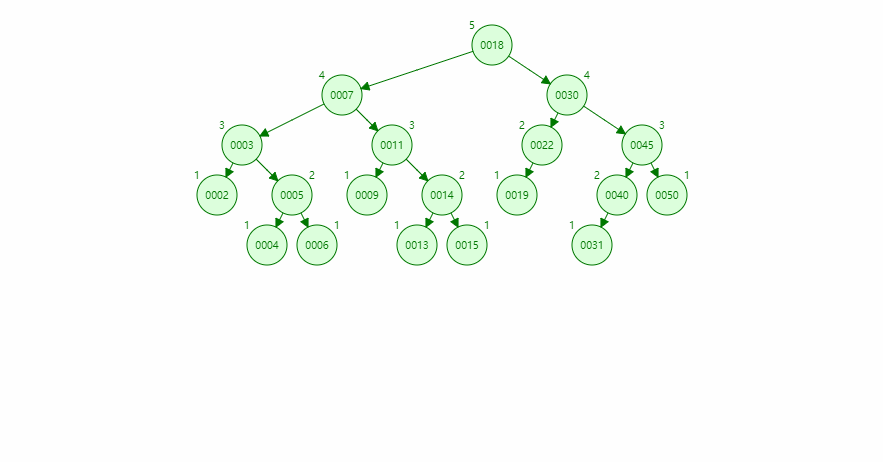
1. AVL简单的理解，如图所示，底部节点为1，不断往上到根节点，数字不断累加。
2. 观察每个节点数字，随意选个节点A，会发现A节点的左子树节点或右子树节点末尾，数到A节点距离之差不会超过1
3. 一旦添加一个数，使得二叉树结构，存在节点两边子树差大于1，若是右子树大，则左旋；左子树大，则右旋。
4. 旋转规则关键节点就是这个A节点，右子树大，则A节点变为左子树，右子节点替代A节点位置并指向A

红黑树

1. 节点是红色或黑色。
2. 根节点是黑色。
3. 每个叶子节点都是黑色的空节点（NIL节点）。
4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

参考 https://www.sohu.com/a/201923614_466939

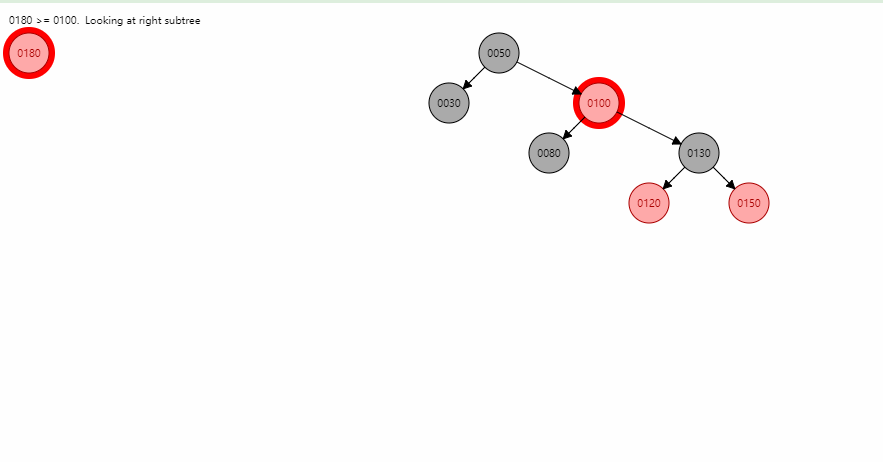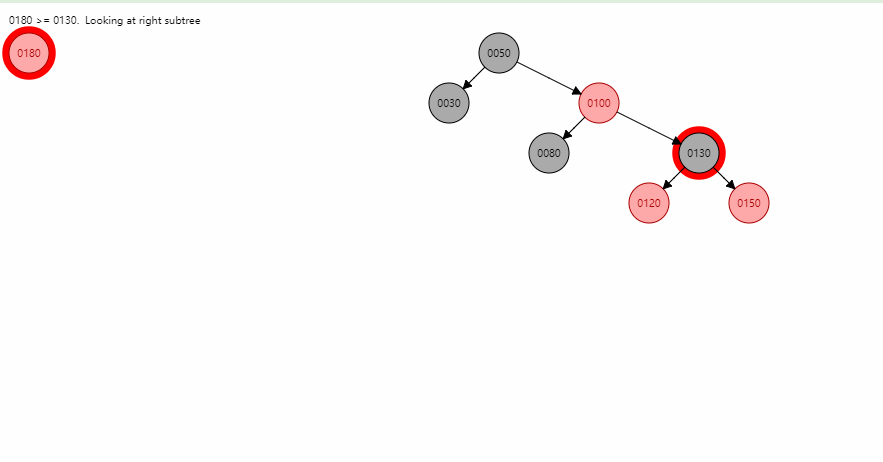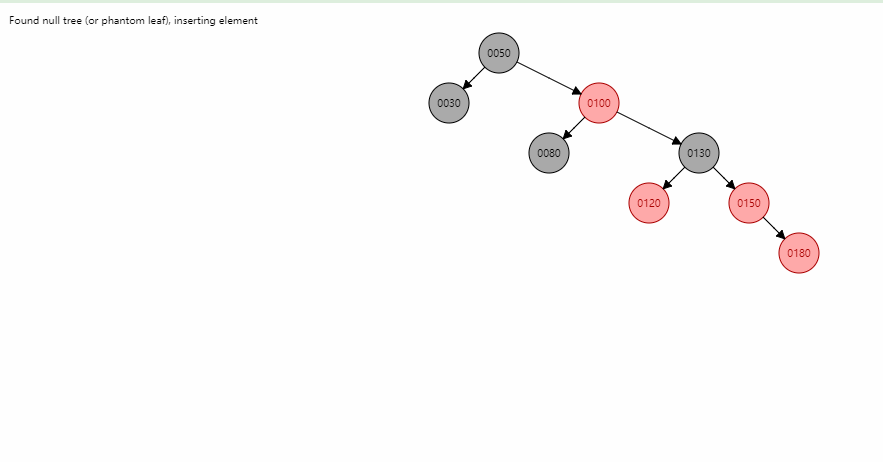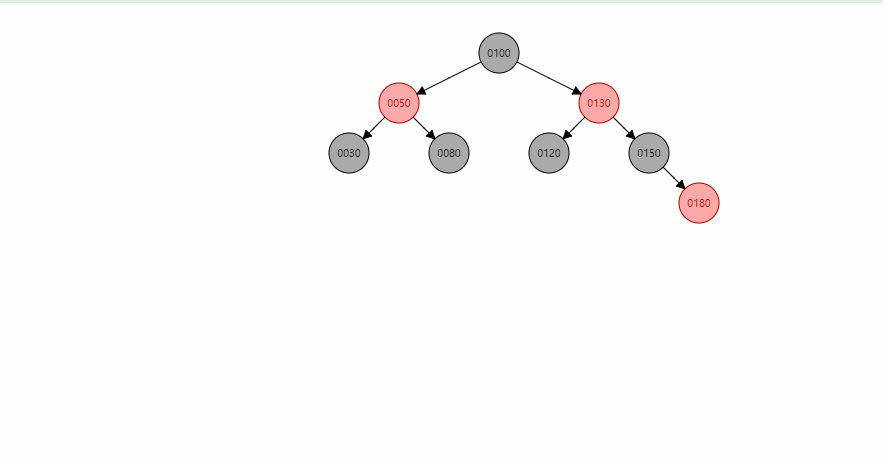
伸展树 - Splay

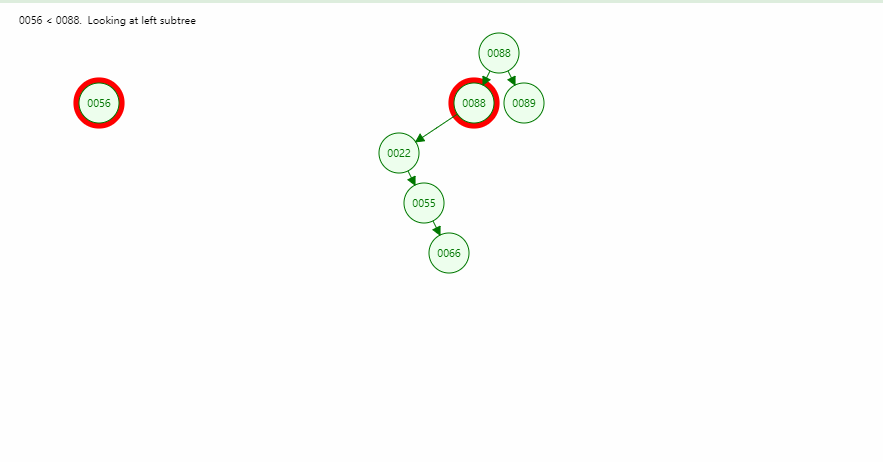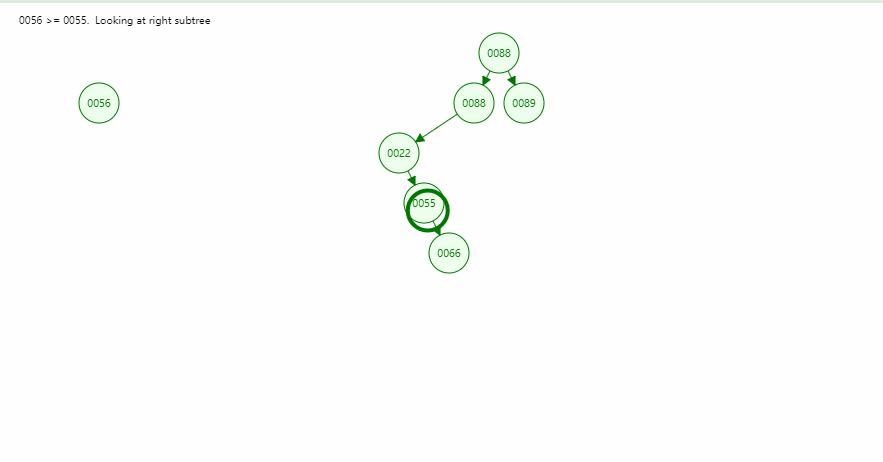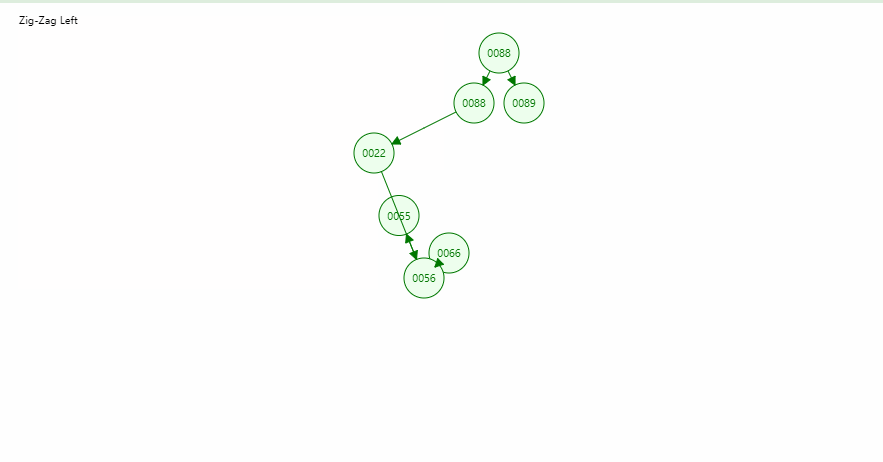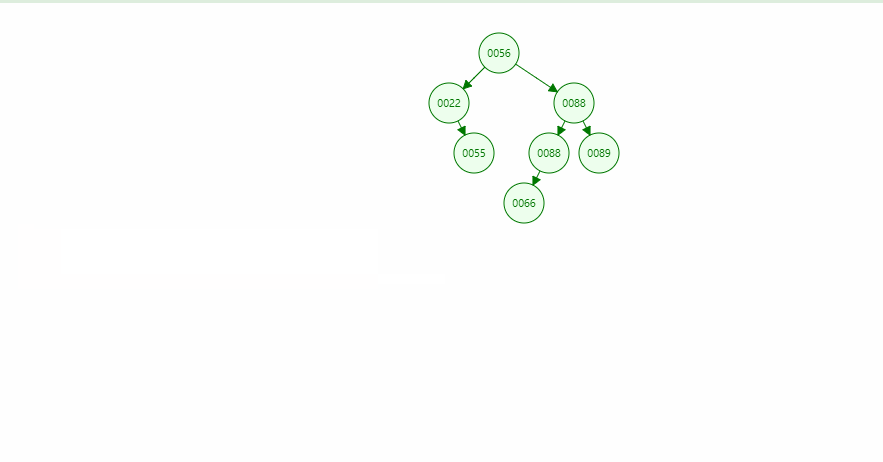
1. 在伸展树上的一般操作都基于伸展操作：假设想要对一个二叉查找树执行一系列的查找操作，为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法， 在每次查找之后对树进行调整，把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。
2. 插入，查找，删除都会经过搬运到树根的过程

哈希表插入 - hash

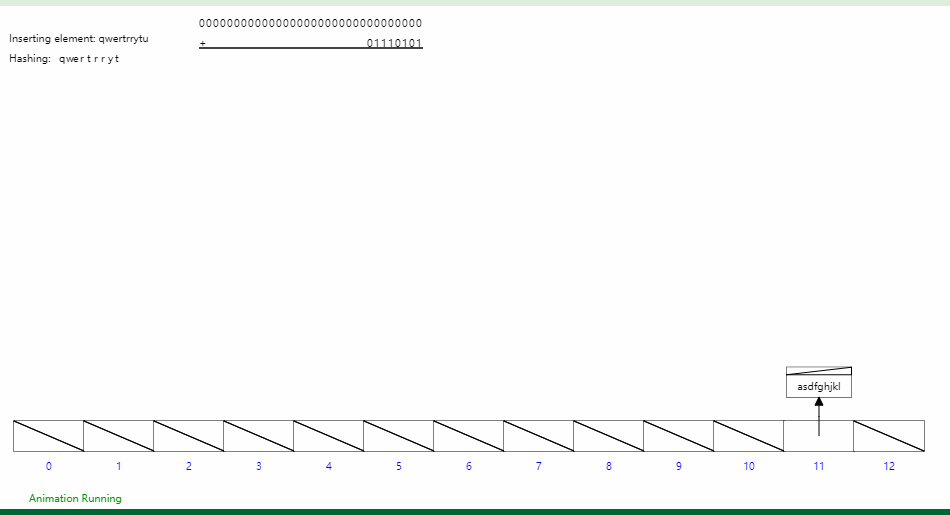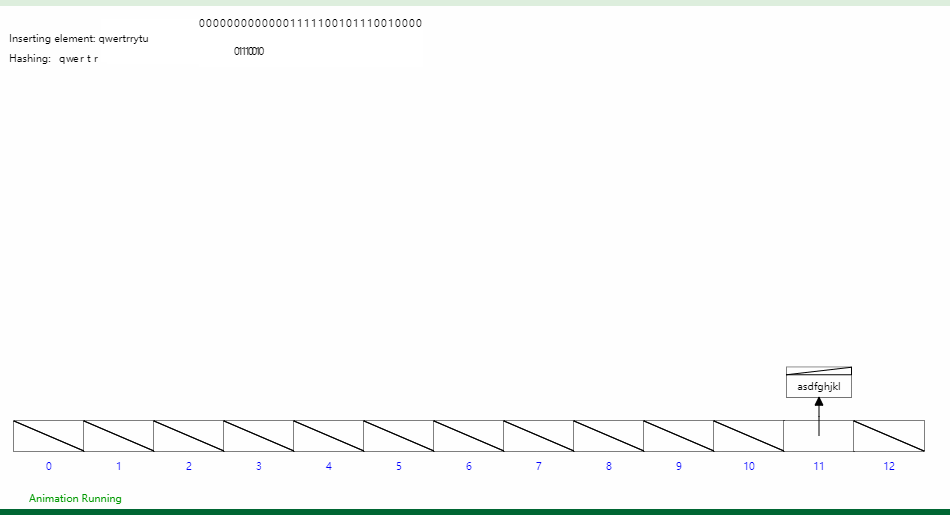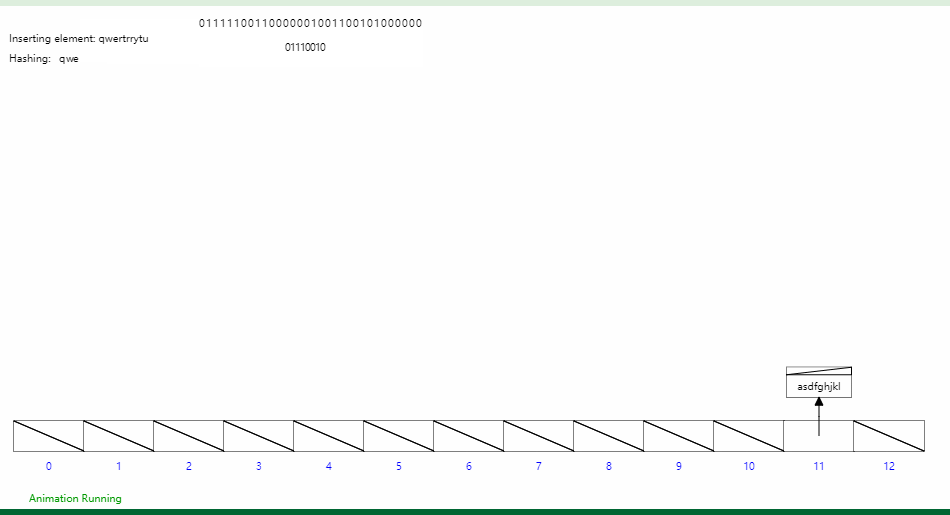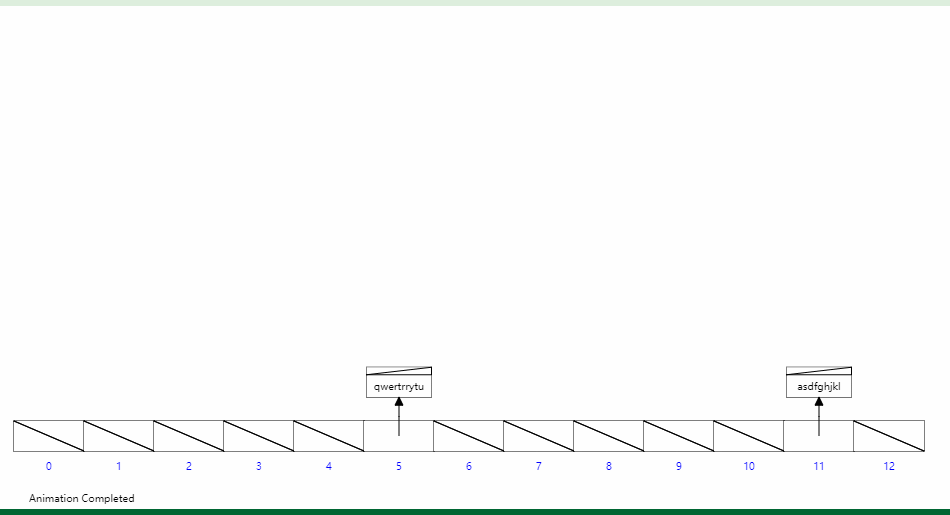
字典树Trie

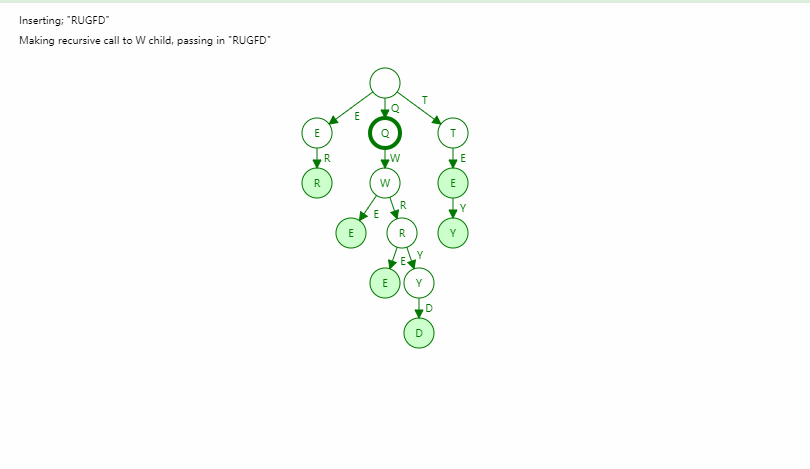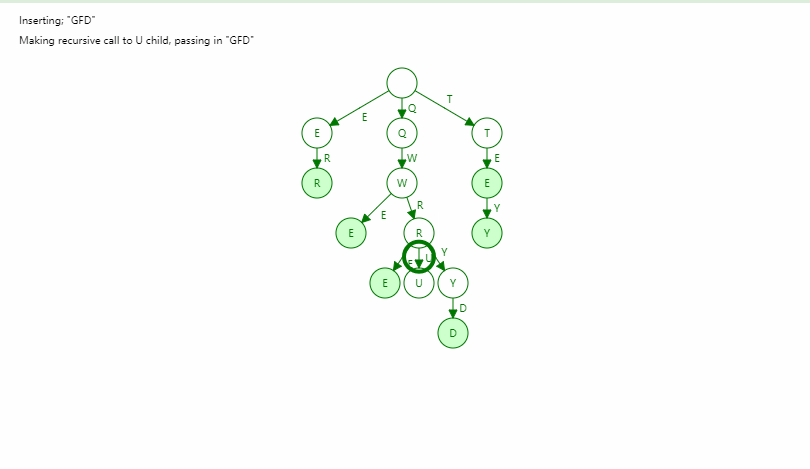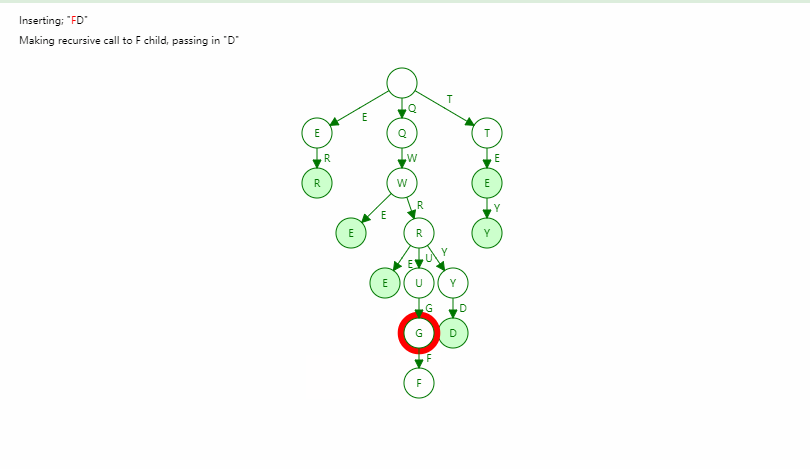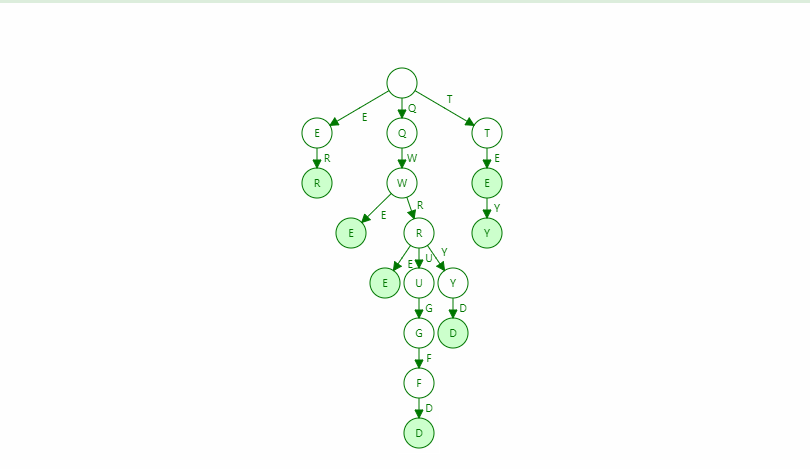
基数树 - Radix Tree

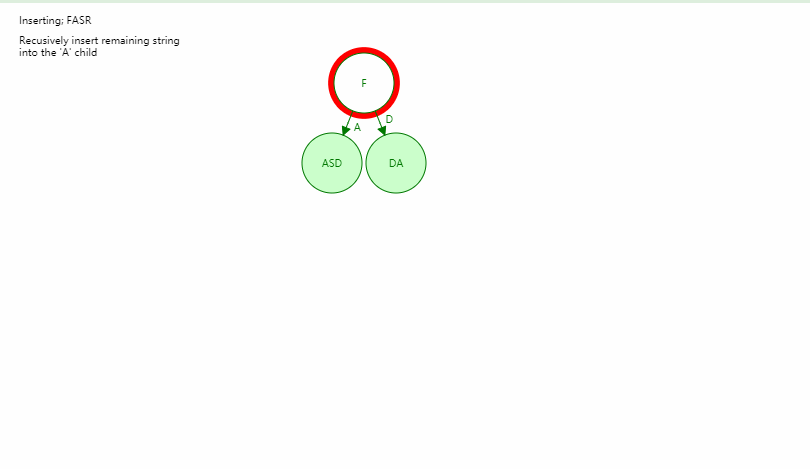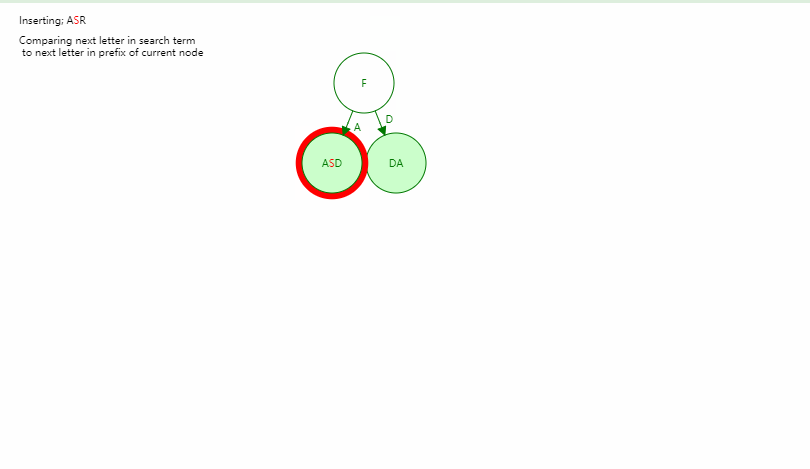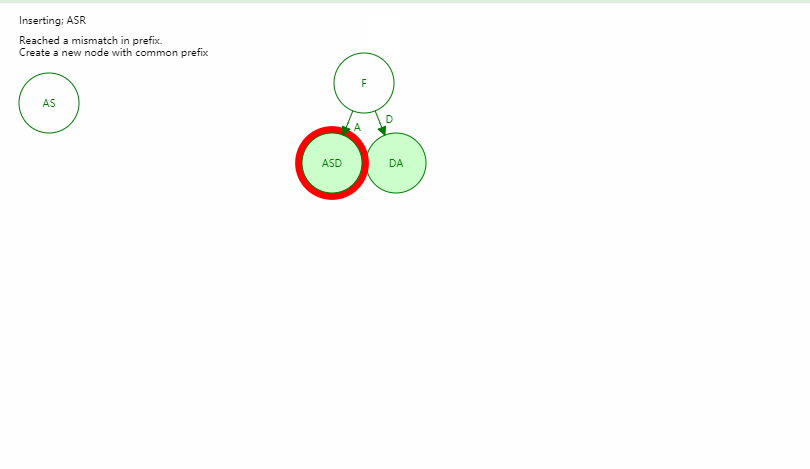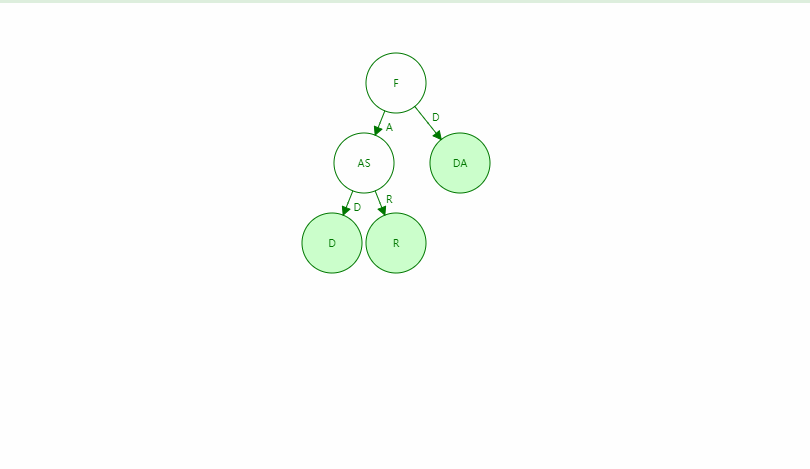
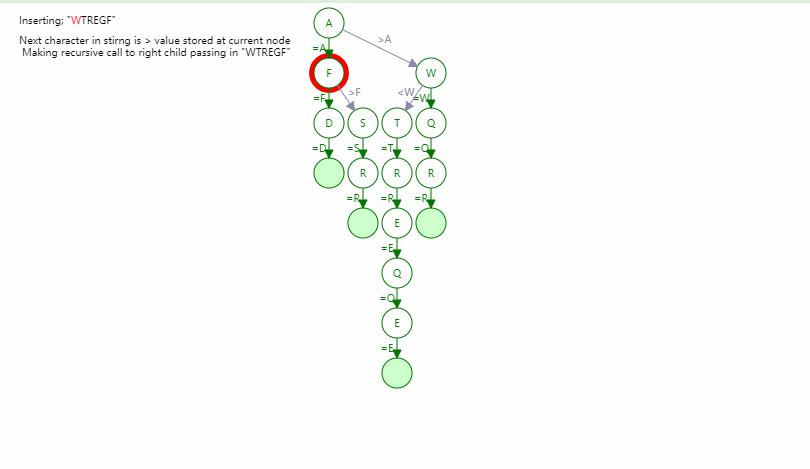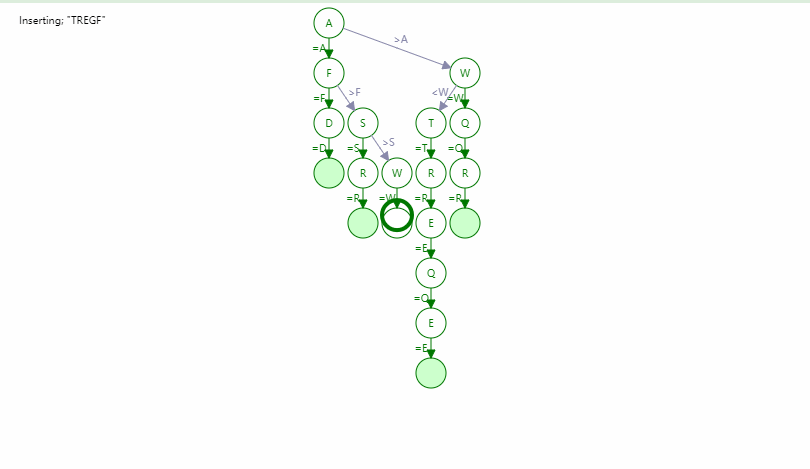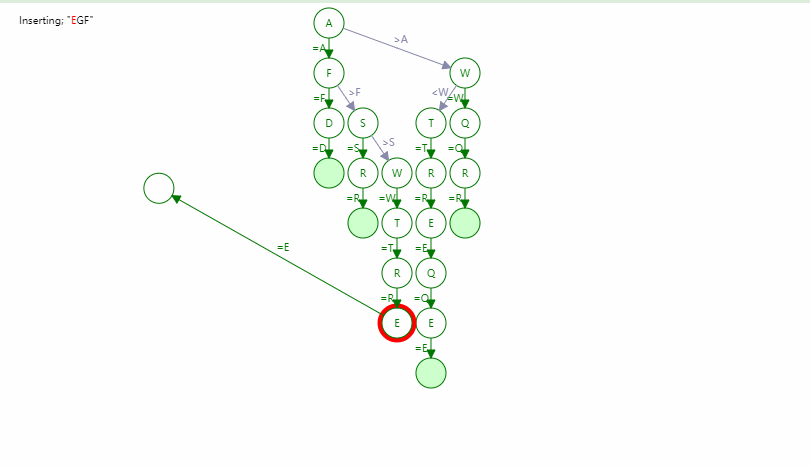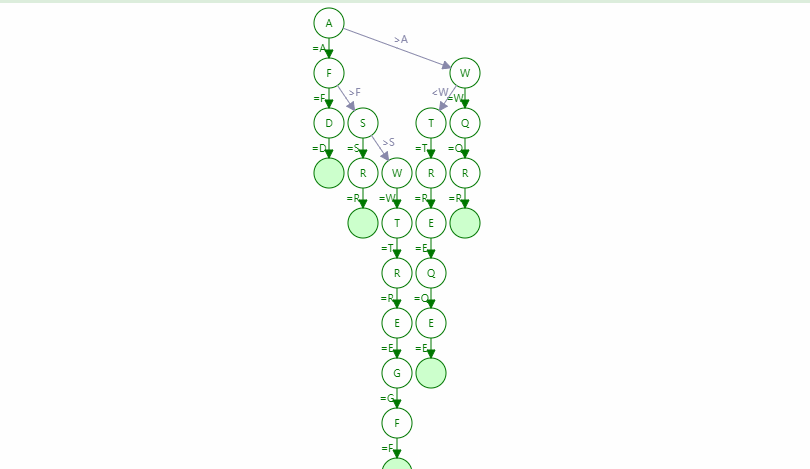
三元搜索树 - Ternary Search Tree

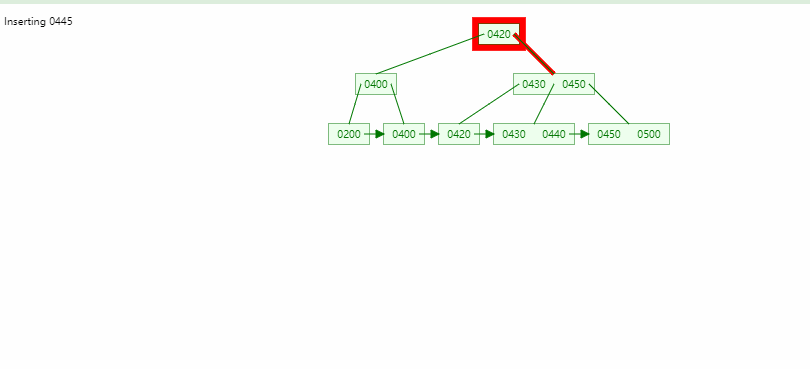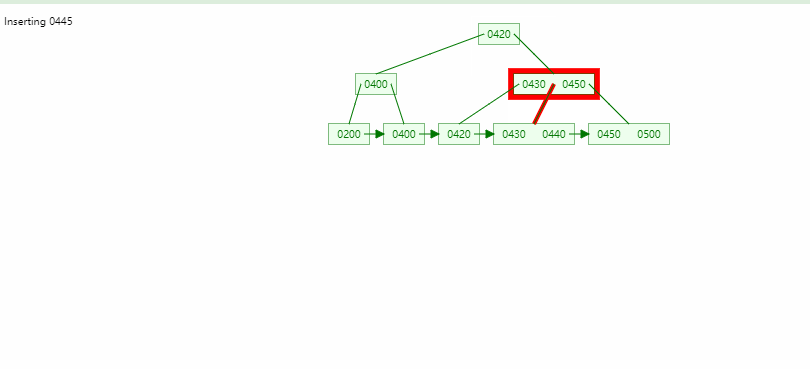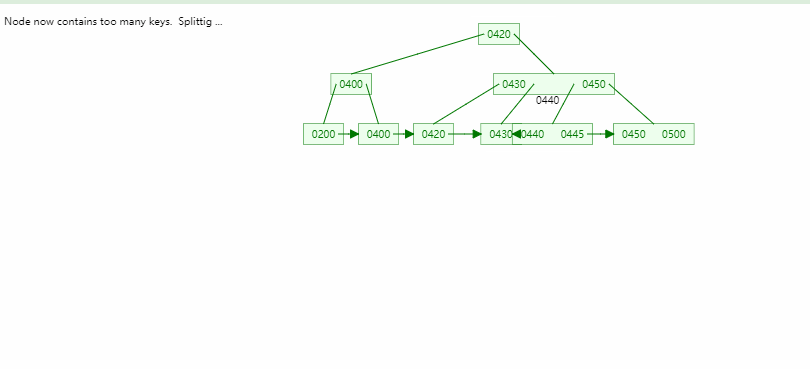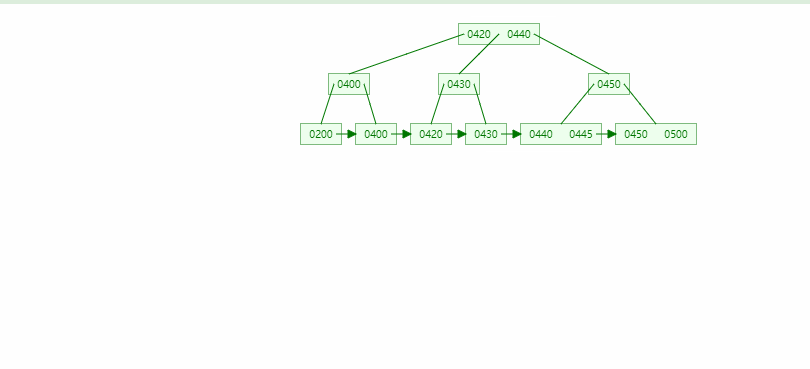
B树

1. B树的平衡性很好，一个节点的最大数量取决于阶数
   

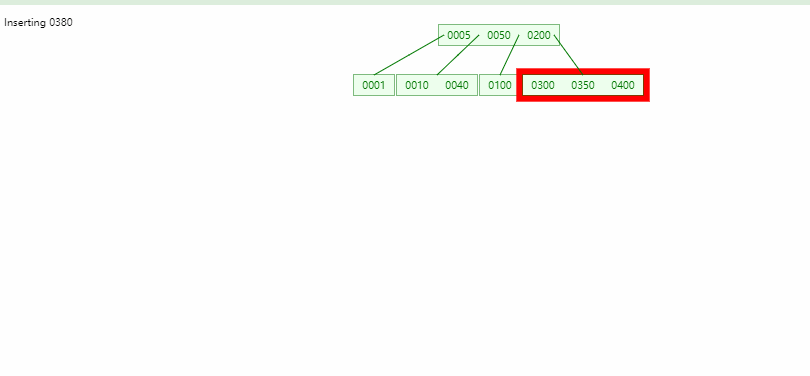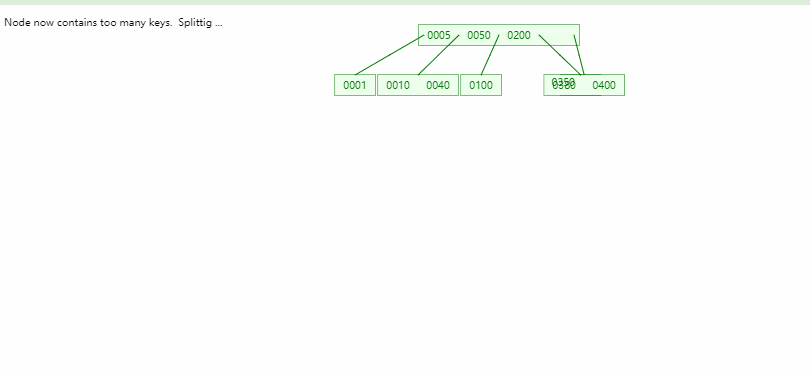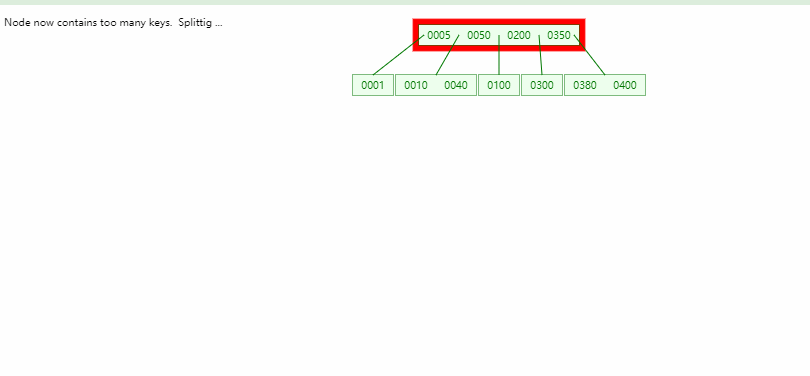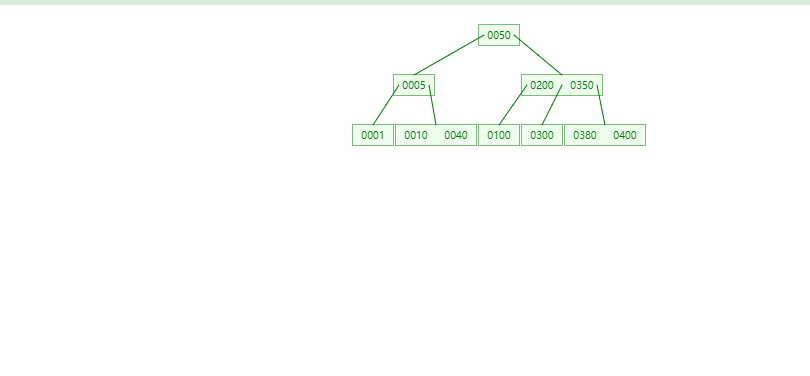
B+树

1. B+树相比B树查询效率更高
   1. b+树的中间节点不保存数据，所以磁盘页能容纳更多节点元素，更“矮胖”；
   2. b+树查询必须查找到叶子节点，b树只要匹配到即可不用管元素位置，因此b+树查找更稳定（并不慢）；
   3. 对于范围查找来说，b+树只需遍历叶子节点链表即可，b树却需要重复地中序遍历