剑指offer（7）

　　今天的几道题目都是关于斐波那契数列的。

　　题目1：

　　大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。

n<=39

　　传统的方法采用递归函数，这种方法也是我们在大学刚刚接触递归函数时老师给的例子。但这种方法会消耗大量的时间和空间，所以在此我们不使用这种方法。

　　思路大致如下图

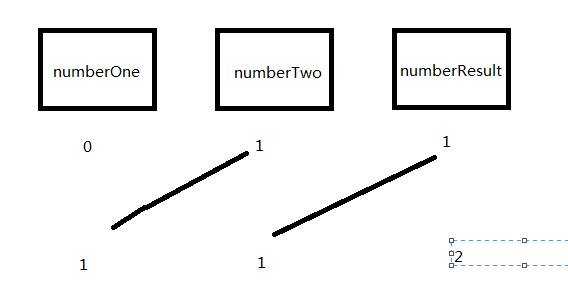
public class Solution {
    public int Fibonacci(int n) {
        int[] a ={0,1};

        if(n<2){
            return a[n];
        }

        int numberOne = 0;
        int numberTwo = 1;
        int numberResult = 0;

        for(int i=2; i<=n; i++){
            numberResult = numberOne + numberTwo;
            numberOne = numberTwo;
            numberTwo = numberResult;
        }

        return numberResult;
    }
}

　　题目2：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

　　先考虑简单情况，如果只有一级台阶，那么结果很显然是1.如果有两级台阶，那么我们就有两个选择了，一种是一次跳一级，跳两次，另外一种是一次跳两级。

　　接着考虑一般情况，把n级台阶时的调发看做n的函数f(n)，当n>2时，如果第一次跳一级那么我们可以表示成1+f(n-1)，若第二次跳两级我们可以表示成2+f(n-2)，第一种情况有f(n-1)种方案，第二种方案有f(n-2)种方案，这样，总体我们就有f(n)=f(n-1)+f(n-2)种方案，不难发现这实际上就是斐波那契数列。

public class Solution {
    public int JumpFloor(int target) {
        int[] a ={0,1,2};

        if(target<=2){
            return a[target];
        }

        int numberOne = 1;
        int numberTwo = 2;
        int numberResult = 0;

        for(int i=3; i<=target; i++){
            numberResult = numberOne + numberTwo;
            numberOne = numberTwo;
            numberTwo = numberResult;
        }

        return numberResult;
    }
}

　　题目3：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

　　这道题目可以沿用上一题的思路，如果只有一级台阶，那么只有一种法案，如果有两级台阶我们就回到了上一题f(2)=f(2-1)+f(2-2)，如果有三级台阶那么我们可以第一次跳一级1+f(3-1)，第一次跳两级2+f(3-2)，或者第一次跳三级3+f(3-3)，可得出f(3)=f(3-1)+f(3-2)+f(3-3)。

　　当有n级台阶时，f(n) = f(0) + f(1) + f(2) + f(3) + ... + f(n-2)+f(n-1)

　　当有n-1级台阶时，f(n-1) = f(0) + f(1) + f(2) + f(3) + ... + f(n-2)

　　不难发现f(n)=2*f(n-1)，一个等比数列，易得f(n)=2^(n-1)

public class Solution {
    public int JumpFloorII(int target) {
        int jumpNumber = 1;
        while((--target)!=0){
            jumpNumber*=2;
        }
        return jumpNumber;
    }
}

　　题目4：

　　我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

　　这题依旧是上面的思想，只是理解上有点小坑。

public class Solution {
    public int RectCover(int target) {
        int a[] = {0,1,2};

        if(target<=2){
            return a[target];
        }

        int numberOne = 1;
        int numberTwo = 2;
        int numberResult = 0;

        for(int i=3;i<=target;i++){
            numberResult = numberOne + numberTwo;
            numberOne = numberTwo;
            numberTwo = numberResult;
        }

        return numberResult;
    }
}