Matrix_tree Theorem 矩阵树定理学习笔记
Matrix_tree Theorem:
给定一个无向图, 定义矩阵A
A[i][j] = - (<i, j>之间的边数)
A[i][i] = 点i的度数
其生成树的个数等于 A的任意n - 1阶主子式的值。
关于定理的相关证明 可以看这篇文章, 讲得非常详细, 耐心看就能看懂：
关于求行列式, 可以用高斯消元。 如果是模域下求行列式, 可以用欧几里得算法。 具体实现看这篇文章
模域下求行列式 模板题：SPOJ DETER3
代码：
#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
using namespace std; #define N 220
#define M 400010
typedef long long ll; const int Mod=;
const double eps = 1e-; ll Solve(ll a[N][N], int n, ll mod)
{
ll res = ;
for (int i = ; i <= n; ++i)
{
for (int j = i; j <= n; ++j)
{
if (a[j][i] < )
{
res *= -;
for (int k = i; k <= n; ++k)
a[j][k] *= -;
}
}
int j;
for (j = i; j <= n && !a[j][i]; ++j);
if (j > n) return ; if (j != i)
{
res = -res;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
} for (j = i + ; j <= n; ++j)
{
while (a[j][i])
{
ll d = a[i][i] / a[j][i];
for (int k = i; k <= n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
res = -res;
}
}
res = res * a[i][i] % mod;
}
if (res < ) res += mod;
return res;
} int main()
{
//freopen("in.in","r",stdin);
//freopen("out.out","w",stdout); int n; ll mod;
while (scanf("%d %lld", &n, &mod) != EOF)
{
ll a[N][N];
for (int i = ; i <= n; ++i)
for (int j = ; j <= n; ++j)
scanf("%lld", &a[i][j]);
printf("%lld\n", Solve(a, n, mod));
} return ;
}
下面给出一些应用(练习题):
应用一：SPOJ HIGH
模板题： 给出一个无向图, 求生成树个数。
代码：
#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
using namespace std; #define N 13
#define M 400010
typedef long long ll; const int Mod=;
const double eps = 1e-; double Solve(int n, double a[N][N])
{
if (n == ) return ; /*for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
printf("%.0lf%c", a[i][j], j == n? '\n':' ');*/ double res = ;
for (int i = ; i <= n; ++i)
{
int j;
for (j = i; j <= n && fabs(a[j][i]) < eps; ++j);
if (j > n) return ;
if (j != i) for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]); for (int j = i + ; j <= n; ++j)
{
double f = a[j][i] / a[i][i];
for (int k = i; k <= n; ++k)
a[j][k] -= f * a[i][k];
}
res *= a[i][i];
} return res;
} int main()
{
//freopen("in.in","r",stdin);
//freopen("out.out","w",stdout); int T, n, m, x, y;
scanf("%d", &T);
while (T--)
{
double a[N][N] = {};
scanf("%d %d", &n, &m);
for (int i = ; i <= m; ++i)
{
scanf("%d %d", &x, &y);
a[x][y]--, a[y][x]--;
a[x][x]++, a[y][y]++;
}
printf("%.0lf\n", Solve(n - , a));
} return ;
}
应用二：BZOJ 4031
构图后 求生成树个数 mod 一个数。
#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
using namespace std; #define N 120
#define M 400010
typedef long long ll; const int Mod=;
const double eps = 1e-; ll Solve(ll a[N][N], int n, ll mod)
{
if (n == ) return ;
ll res = ;
for (int i = ; i <= n; ++i)
{
//for (int p = 1; p <= n; ++p)
// for (int q = 1; q <= n; ++q)
// printf("%lld%c", a[p][q], q == n? '\n':' '); for (int j = i; j <= n; ++j)
{
if (a[j][i] < )
{
res = -res;
for (int k = i; k <= n; ++k) a[j][k] *= -;
}
} int j;
for (j = i; j <= n && !a[j][i]; ++j);
if (j > n) return ; if (j != i)
{
res = -res;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
} for (j = i + ; j <= n; ++j)
{
while (a[j][i])
{
ll d = a[i][i] / a[j][i];
for (int k = i; k <= n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
res = -res;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
}
}
res = res * a[i][i] % mod;
// printf("res = %lld\n", res);
}
if (res < ) res += mod;
// cout << "aa= "<<res <<endl;
return res;
} int main()
{
//freopen("in.in","r",stdin);
//freopen("out.out","w",stdout); int n, m; ll mod = ;
char mp[][]; int tot = ;
int id[][];
scanf("%d %d", &n, &m);
for (int i = ; i <= n; ++i)
{
for (int j = ; j <= m; ++j)
{
scanf(" %c", &mp[i][j]);
if (mp[i][j] == '.') id[i][j] = ++tot;
}
}
ll a[N][N] = {};
for (int i = ; i < n; ++i)
{
for (int j = ; j <= m; ++j)
{
if (mp[i][j] == '.' && mp[i + ][j] == '.')
{
int x = id[i][j], y = id[i + ][j];
a[x][y]--, a[y][x]--;
a[x][x]++, a[y][y]++;
}
}
}
for (int i = ; i <= n; ++i)
{
for (int j = ; j < m; ++j)
{
if (mp[i][j] == '.' && mp[i][j + ] == '.')
{
int x = id[i][j], y = id[i][j + ];
a[x][y]--, a[y][x]--;
a[x][x]++, a[y][y]++;
}
}
}
printf("%lld\n", Solve(a, tot - , mod));
return ;
}
应用三： BZOJ 2467
这题数据范围比较小,可以暴力建图 然后跑Matrix tree。
另外可以直接推公式：
一共有4n个点, 5n条边, 所以要删去n - 1条边, 然后可以发现 每个五边形外面的4条边最多只能删一条。
根据鸽笼原理合法的解 一定是 有一个五边形删去了里面的那条边 和外面的某条边, 其余的五边形删去了任意一条边。
所以答案就是$4*n*5^{n-1}$
Matrix tree 代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
using namespace std; #define X first
#define Y second
#define N 420
#define M 11 typedef long long ll;
const int Mod = ;
const int INF = << ; void Add(int x, int y, int &tot, int a[N][N])
{
a[x][tot + ] = a[tot + ][x] = -;
a[tot + ][tot + ] = a[tot + ][tot + ] = -;
a[tot + ][tot + ] = a[tot + ][tot + ] = -;
a[tot + ][y] = a[y][tot + ] = -;
a[tot + ][tot + ] = a[tot + ][tot + ] = a[tot + ][tot + ] = ;
a[x][x] = a[y][y] = ; tot += ;
a[x][y]--,a[y][x]--;
} int Solve(int n, int a[N][N], int mod)
{ if (n == ) return ;
int res = ;
for (int i = ; i <= n; ++i)
{
for (int j = i; j <= n; ++j)
{
if (a[j][i] < )
{
res = -res;
for (int k = i; k <= n; ++k) a[j][k] = -a[j][k];
}
}
//cout << i << endl;
//for (int p = 1; p <= n; ++p)
// for (int q = 1; q <= n; ++q)
// printf("%d%c", a[p][q], q == n? '\n':' ');
//printf("\n");
int j;
for (j = i; j <= n && !a[j][i]; ++j);
if (j > n) return ;
if (i != j)
{
res = -res;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
} for (j = i + ; j <= n; ++j)
{
while (a[j][i])
{
int d = a[i][i] / a[j][i];
for (int k = i; k <= n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
res = -res;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
}
}
res = res * a[i][i] % mod;
}
if (res < ) res += mod;
return res;
} int main()
{
//freopen("in.in","r",stdin);
//freopen("out.out","w",stdout); int T; scanf("%d", &T);
while (T--)
{
int n, mod = , tot, a[N][N] = {}; scanf("%d", &n); tot = n;
for (int i = ; i < n; ++i) Add(i, i + , tot, a);
Add(n, , tot, a);
printf("%d\n", Solve(tot - , a, mod));
}
return ;
}
应用四：BZOJ 1016
题目大意：求最小生成树个数。
性质一：无向图所有MST中，相同权值的边数一样多。
证明看https://blog.sengxian.com/solutions/bzoj-1016
性质二：对于任意MST，加入所有权值<=w的边后, 形成的森林连通性相同 。
证明：
考虑Kruskal算法的过程，我们首先会尽可能多的加入权值最小的边。这个过程相当于拿出所有权值最小的边，然后任意求一颗生成树，因此我们可以知道，能加入的权值最小的边的数量是一定的，而且加入这些边之后 形成的森林连通性相同。
结合性质一，对于任意一棵MST，因为它包含的权值最小的边数和做Kruskal算法求出的MST包含的边数是一样的，这些边又不能形成环，因此这些边形成的森林和 做Kruskal时形成的森林连通性是一样的。 对于任意MST，加入所有权值最小的边后, 形成的森林连通性相同 。
然后我们考虑把已经形成的联通块缩点， 考虑所有权值第二小的边，重复上面的过程，可以证明对于任意MST，加入所有权值<=w的边后, 形成的森林连通性相同 。
所以我们的算法就可以模拟这个过程, 把边按权值从小到大排好序, 每次加入权值相同的所有边, 形成一些连通块， 然后对于每个连通块, 跑Matrix tree 求出形成这个连通块有多少种方案。 统计好之后每个连通块缩点, 进行下一种权值的边的加边操作。 代码实现起来还是挺多细节的。
代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
using namespace std; #define X first
#define Y second
#define N 120
#define M 1010 typedef long long ll;
const int Mod = ;
const int INF = << ; struct Edge
{
int x, y, z;
bool operator < (const Edge &t)const{return z < t.z;}
}e[M]; int Solve(int n, int a[N][N], int mod)
{
if (n == ) return ;
int res = ;
for (int i = ; i < n; ++i)
{
for (int j = i; j < n; ++j)
{
if (a[j][i] < )
{
res = -res;
for (int k = i; k < n; ++k) a[j][k] = -a[j][k];
}
}
int j;
for (j = i; j < n && !a[j][i]; ++j);
if (j == n) return ;
if (i != j)
{
res = -res;
for (int k = i; k < n; ++k) swap(a[i][k], a[j][k]);
} for (j = i + ; j < n; ++j)
{
while (a[j][i])
{
int d = a[i][i] / a[j][i];
for (int k = i; k < n; ++k) a[i][k] -= d * a[j][k] % mod, a[i][k] %= mod;
res = -res;
for (int k = i; k < n; ++k) swap(a[i][k], a[j][k]);
}
}
res = res * a[i][i] % mod;
}
if (res < ) res += mod;
return res;
} int father[N], id[N], pa[N], num[N];
vector<int> lis[N];
vector<pair<int, int> > ed[N]; int Find(int x)
{
if (father[x] == x) return x;
father[x] = Find(father[x]);
return father[x];
} void Merge(int x, int y)
{
x = Find(x), y = Find(y);
if (x != y) father[x] = y;
} int main()
{
//freopen("in.in","r",stdin);
//freopen("out.out","w",stdout); int n, m, mod = ;
scanf("%d %d", &n, &m);
for (int i = ; i <= m; ++i) scanf("%d %d %d", &e[i].x, &e[i].y, &e[i].z);
sort(e + , e + m + ); int res = , block = n;
for (int i = ; i <= n; ++i) id[i] = i;
for (int l = , r; l <= m;)
{
for (r = l; r < m && e[r + ].z == e[l].z; ++r);
for (int i = ; i <= block; ++i) father[i] = i;
for (r = l; r < m && e[r + ].z == e[l].z; ++r);
for (int i = l; i <= r; ++i) Merge(id[e[i].x], id[e[i].y]); int tot = ;
for (int i = ; i <= block; ++i) if (father[i] == i) pa[i] = ++tot;
for (int i = ; i <= block; ++i) pa[i] = pa[Find(i)];
for (int i = ; i <= block; ++i) lis[pa[i]].push_back(i), num[i] = lis[pa[i]].size() - ;
for (int i = l; i <= r; ++i)
{
int x = id[e[i].x], y = id[e[i].y];
if (x == y) continue;
ed[pa[x]].push_back(make_pair(num[x], num[y]));
}
for (int i = ; i <= tot; ++i)
{
int a[N][N] = {}, x, y;
for (int j = ; j < ed[i].size(); ++j)
{
x = ed[i][j].X, y = ed[i][j].Y;
a[x][x]++, a[y][y]++;
a[x][y]--, a[y][x]--;
}
res = res * Solve(lis[i].size() - , a, mod) % mod;
} for (int i = ; i <= n; ++i) id[i] = pa[id[i]];
for (int i = ; i <= tot; ++i) lis[i].clear(), ed[i].clear();
block = tot; l = r + ;
}
if (block > ) puts("");
else printf("%d\n", res);
return ;
}
应用五： BZOJ 3534 Matrix Tree Theorem 的扩展, 非常精彩的题。
题目大意：
给出一个无向图, 两点之间的连边会有一个概率， 求连成一颗树的概率。
这个题如果没有看过Matrix Tree Theorem定理的证明,只是记住结论 应该是做不出来的。。。
先来看一个简化版本：
给出一个无向图, 定义它的一棵生成树的权值为所有边权的乘积。 求所有生成树的权值和。 ( 原题还要考虑一些边不选的概率 这题只靠考虑选的边）
参考最前面给出的 证明Matrix Tree Theorem定理的文章。
原来是
A[i][j] = - (<i, j>之间的边数)
A[i][i] = 点i的度数
现在改成
A[i][j] = - (<i, j>之间的所有边权和)
A[i][i] = 和i相连的所有边的边权和
修改关联矩阵B的定义, 把1 改成 $e_j$的边权开根号后的值。
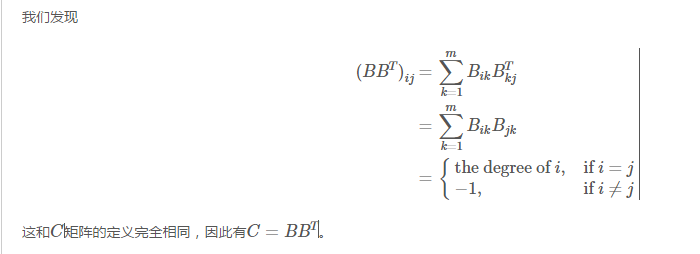
这里也做相应的修改, 把 -1 改成 -<i,j>之间的边权和, the degree of i 改成和i相连的所有边的边权和。
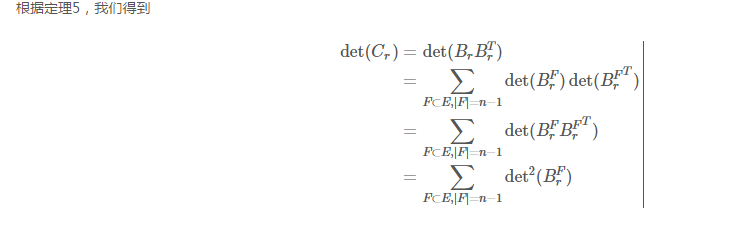
做了以上修改之后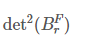
刚好就是所选的生成树的边权的乘积。
所以用修改后的A数组跑Matrix Tree就可以解决这个问题了。
当然原题 还要乘上 其他边不选的概率。 再对A数组做点小修改就好了。具体实现看代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
using namespace std; #define X first
#define Y second
#define N 100
#define M 11 typedef long long ll;
const int Mod=;
const int INF=<<; const double eps = 1e-; double Solve(double a[N][N], int n)
{
if (n == ) return ;
double res = ;
for (int i = ; i <= n; ++i)
{
int j = i;
for (int k = i + ; k <= n ; ++k) if (fabs(a[k][i]) > fabs(a[j][i])) j = k;
if (fabs(a[j][i]) < eps) return ;
if (i != j)
{
res = -res;
for (int k = i; k <= n; ++k) swap(a[i][k], a[j][k]);
} for (j = i + ; j <= n; ++j)
{
double f = a[j][i] / a[i][i];
for (int k = i; k <= n; ++k) a[j][k] -= f * a[i][k];
}
res *= a[i][i];
}
return res;
} int main()
{
//freopen("in.in","r",stdin);
//freopen("out.out","w",stdout); int n;
double a[N][N] = {}, res = ; scanf("%d", &n);
for (int i = ; i <= n; ++i)
{
for (int j = ; j <= n; ++j)
{
scanf("%lf", &a[i][j]);
if (i == j) continue;
if (i < j && fabs(a[i][j] - ) > eps) res *= - a[i][j];
if (fabs(a[i][j] - ) > eps) a[i][j] = -a[i][j] / ( - a[i][j]);
else a[i][j] = -a[i][j];
}
}
for (int i = ; i <= n; ++i)
for (int j = ; j <= n; ++j)
if (i != j) a[i][i] -= a[i][j];
printf("%.8lf\n", fabs(res * Solve(a, n - )));
return ;
}
Matrix_tree Theorem 矩阵树定理学习笔记的更多相关文章
- [HEOI2015]小Z的房间(矩阵树定理学习笔记)
题目描述 你突然有了一个大房子,房子里面有一些房间.事实上,你的房子可以看做是一个包含n*m个格子的格状矩形,每个格子是一个房间或者是一个柱子.在一开始的时候,相邻的格子之间都有墙隔着. 你想要打通一 ...
- 洛谷4455 [CQOI2018]社交网络 (有向图矩阵树定理)(学习笔记）
sro_ptx_orz qwq算是一个套路的记录 对于一个有向图来说 如果你要求一个外向生成树的话,那么如果存在一个\(u\rightarrow v\)的边 那么\(a[u][v]--,a[v][v] ...
- 矩阵树定理&BEST定理学习笔记
终于学到这个了,本来准备省选前学来着的? 前置知识:矩阵行列式 矩阵树定理 矩阵树定理说的大概就是这样一件事:对于一张无向图 \(G\),我们记 \(D\) 为其度数矩阵,满足 \(D_{i,i}=\ ...
- Note -「矩阵树定理」学习笔记
大概--会很简洁吧 qwq. 矩阵树定理 对于无自环无向图 \(G=(V,E)\),令其度数矩阵 \(D\),邻接矩阵 \(A\),令该图的 \(\text{Kirchhoff}\) 矩阵 \ ...
- [专题总结]矩阵树定理Matrix_Tree及题目&题解
专题做完了还是要说两句留下什么东西的. 矩阵树定理通俗点讲就是: 建立矩阵A[i][j]=edge(i,j),(i!=j).即矩阵这一项的系数是两点间直接相连的边数. 而A[i][i]=deg(i). ...
- [spoj104][Highways] (生成树计数+矩阵树定理+高斯消元)
In some countries building highways takes a lot of time... Maybe that's because there are many possi ...
- 【LOJ#6072】苹果树（矩阵树定理，折半搜索，容斥）
[LOJ#6072]苹果树(矩阵树定理,折半搜索,容斥) 题面 LOJ 题解 emmmm,这题似乎猫讲过一次... 显然先\(meet-in-the-middle\)搜索一下对于每个有用的苹果数量,满 ...
- 【算法】Matrix - Tree 矩阵树定理 & 题目总结
最近集中学习了一下矩阵树定理,自己其实还是没有太明白原理(证明)类的东西,但想在这里总结一下应用中的一些细节,矩阵树定理的一些引申等等. 首先,矩阵树定理用于求解一个图上的生成树个数.实现方式是:\( ...
- CF917D. Stranger Trees & TopCoder13369. TreeDistance（变元矩阵树定理＋高斯消元）
题目链接 CF917D:https://codeforces.com/problemset/problem/917/D TopCoder13369:https://community.topcoder ...
随机推荐
- Android常用传感器用法一览(1)
1.传感器入门自从苹果公司在2007年发布第一代iPhone以来,以前看似和手机挨不着边的传感器也逐渐成为手机硬件的重要组成部分.如果读者使用过iPhone.HTC Dream.HTC Magic.H ...
- Win7如何关闭操作中心的图标
运行gpedit.msc,打开组策略编辑器 双击"删除操作中心图标",将其启用即可(重启可见)
- rapidxml的常见读写操作
rapidxml官网地址:http://rapidxml.sourceforge.net/ rapidxml只包含4个hpp头文件,把这四个头文件放到项目中,即可使用rapidxml #include ...
- Android 如何在关于手机界面添加个图片
前言 欢迎大家我分享和推荐好用的代码段~~ 声明 欢迎转载,但请保留文章原始出处: CSDN:http://www.csdn.net ...
- JQUERY插件学习之jQuery UI
jQuery UI:http://jqueryui.com/ jQuery UI介绍: jQuery UI 是以 jQuery 为基础的开源 JavaScript 网页用户界面代码库.包含底层用户交互 ...
- 改动Dialog窗口的类名
VS2013 的MFC project(project名: MobileLink).想要改动窗口的类名时,发现不是像设置窗口名一样调用一个函数能够实现的. 实现的注意问题,请看凝视. (1) 改 ...
- 算法笔记_083:蓝桥杯练习 合并石子（Java）
目录 1 问题描述 2 解决方案 1 问题描述 问题描述 在一条直线上有n堆石子,每堆有一定的数量,每次可以将两堆相邻的石子合并,合并后放在两堆的中间位置,合并的费用为两堆石子的总数.求把所有石子 ...
- vscode Gitlens插件 查看代码提交
GitLens
- 类非静态成员的函数指针 的使用 Function pointer of a non-static member function of a class
you can get the pointer of the method, but it has to be called with an object typedef void (T::*Meth ...
- linux安装php sphinx出错
安装sphinx的php客户端 # wget -c http://pecl.php.net/get/sphinx-1.3.0.tgz # .tgz # cd sphinx- # phpize # ./ ...