【神仙题】【P4885】 灭顶之灾

传送门

Description

请将题目名称的首字母连起来读

Scarlet有一张$n*m$的神秘表格。现在Scarlet向表格中填数字，她会从第一行中的某个格子起，按照从左往右，从上往下的顺序依次填写从$1$开始的正整数，直至填满最后一行。

为了让你确定这个表格，Scarlet会告诉你表格中的$s$组同行连续数字。之后，Scarlet会对你发起$q$次询问，你需要依次回答每个数字被填在第几行第几列中。

Input

第一行$4$个正整数分别代表$n,m,s,q$

接下来$s$行，每行两个正整数$a_i,b_i$，代表整数$a_i$到$b_i$在表格中处于同一行且连续

接下来$q$行，每行一个正整数$A_i$，表示每个询问的数字

Output

如果符合数据的表格不存在，输出一行“Impossible!”（不含引号）

再如果符合数据的表格不唯一，输出一行"Uncertain!"（不含引号）

否则输出$q$行，每行两个正整数，代表每个被询问的数字被填在第几行第几列，如果该数字不在表格内，输出"0 0"

Scarlet为了减小输出文件，以轻易地上传测试数据至服务器，她现在只需要你输出所有行列数据的异或和（包括前文的“0 0”）。

Sample Input

3 4 2 2
8 9
2 4
9
3

Sample Output

7

Hint

对于100%的数据，$1\leq n,m,A_i,a_i,b_i\leq 10^{18}$，$1\leq s,q\leq 5*10^5$，$0\leq b_i-a_i\leq m-1$

Solution

推式子……瞎搞……想明白细节还是很恶心……

考虑对于每一个形如\(a,b\)在同一行的信息，都提供了一个\(a\)所能出现的区间。具体的，考虑在一列中，\(a\)最靠左能出现在第\(1\)行，最靠右能出现在第\(m-(b-a)\)行（此时\(b\)在第\(m\)行）。如果从左向右，从上向下数，设\(1\)前面有\(x\)个\(0\)，那么\(a\)是矩阵中第\(a+x\)个数。这就给出了我们一个方程：

\[(a+x)~Mod~m~\in~[1,m-b+a]
\]

将\(a\)移项，化简可得：

\[x~Mod~M~\in~[1-a,m-b]
\]

由此可以解出x的值。

显然分别对于所有的信息解方程，最后留下的\(x\)就是\(x\)能取到的值。当这个值的个数为\(0\)时无解，大于\(1\)时有多组解（矩阵不唯一）

考虑对于每个解集如何求交。

由于是一个模意义下的解，\(x\)的解集共有两种情况，第一种情况形如\(x~\in~[l,r]\)，第二种情况形如\(x~\in~[0,l]~\bigcup~[r,m-1]\)。对于第一种情况显然可以直接对每个解集求交。考虑第二种情况，能否通过单独维护左右两个区间的交集，最后与第一种情况分别相交再取并集得到答案呢？事实上是不能的。考虑如图的解集：



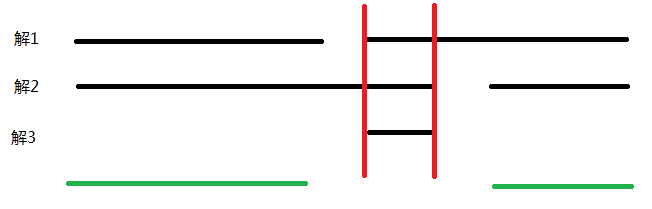
其中解1、2、3分别是解不等式得到的解集区间。显然他们的交集是被红色区域框柱的一部分。如果对左右部分分别求交，得到的区间会是绿色线段。再与解3求交后求并的结果是空集。答案错误。

正确的姿势应该是对每个解维护补集的并集。最后对并集求补集，所有解的交集。如果您不能理解上面的话，请多读几遍画个图。维护答案的方法使用数组存储并集即可，然后按照左端点排序，扫描一遍数组，对于覆盖线段树数为\(0\)的区间累加ans即可得到答案。

对于目前的数据这样的代码交上去即可AC。但是需要注意的是这样的算法存在瑕疵。考虑下面的数据：

2 2 2 1
4 4
2 3
1

正确答案显然应该输出\("Impossible!"\)

但事实上对于一部分代码这样的数据会输出一个答案3。输出x的解集你会发现计算机算出来的矩阵长这样：

0 1
2 3
4 5

这显然是不合法的，因为他的行数不合要求。但是我们在计算矩阵的时候并没有考虑行数的限制。解决方法很简单，对于所有一定出现在最后一行的数字（即\(b~\geq (n-1)~\times~m\)），对\(x\)的范围再做一个限制。具体的，设\(t=n~\times~m~-b\)，则一定不会有大于\(t\)个\(0\)出现，添加限制\(x~\leq~t\)即可。在代码中，因为我脑子有毛病，所以用了另一个计算这个限制的方法，十分脑残但是懒得改了= =。

由此计算出的\(x\)，便可作为正确的答案。

Code

在实现中，因为两个1e18相乘会爆long long，\((n-1)~\times~m\)使用int128存储。

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define rg register
#define ci const int
#define cl const long long int

typedef long long int ll;

namespace IO {
    char buf[90];
}

template<typename T>
inline void qr(T &x) {
    char ch=getchar(),lst=' ';
    while(ch>'9'||ch<'0') lst=ch,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    if(lst=='-') x=-x;
}

template<typename T>
inline void write(T x,const char aft,const bool pt) {
    if(x<0) x=-x,putchar('-');
    int top=0;
    do {
        IO::buf[++top]=x%10+'0';
        x/=10;
    } while(x);
    while(top) putchar(IO::buf[top--]);
    if(pt) putchar(aft);
}

template<typename T>
inline T mmax(const T a,const T b) {if(a>b) return a;return b;}
template<typename T>
inline T mmin(const T a,const T b) {if(a<b) return a;return b;}
template<typename T>
inline T mabs(const T a) {if(a<0) return -a;return a;}

template<typename T>
inline void mswap(T &a,T &b) {
    T temp=a;a=b;b=temp;
}

const int maxn = 1000010;

struct Zay {
    ll x;int y;
    inline bool operator<(const Zay &_others) const {
        return this->x < _others.x;
    }
};
Zay MU[maxn];

ll n,m,ans,cnt;
int s,q;
__int128 uc,tp;

ll check();

int main() {
    qr(n);qr(m);qr(s);qr(q);
    rg ll a,b,l1=0,r1=m-1;
    uc=n-1;uc*=m;
    while(s--) {
        a=b=0;qr(a);qr(b);
        if((1.0*b)/n > (1.0*m)) {puts("Impossible!");return 0;}
        a%=m;
        ll tl=((1ll-a)%m+m)%m,tr=((m-b)%m+m)%m;
        if(tl <= tr) l1=mmax(l1,tl),r1=mmin(r1,tr);
        else {
            MU[++cnt]=(Zay) {tr+1,1};
            MU[++cnt]=(Zay) {tl-1,-1};
        }
        tp=b;
        if(tp > uc) {MU[++cnt]=(Zay) {m-(int)(tp-uc)+1,1};MU[++cnt]=(Zay) {m+1,-1};}
    }
    MU[++cnt]=(Zay) {-1,1};MU[++cnt]=(Zay) {l1-1,-1};MU[++cnt]=(Zay) {r1+1,1};MU[++cnt]=(Zay) {m+1,-1};
    rg ll k;
    std::sort(MU+1,MU+1+cnt);
    k=check();
    while(q--) {
        a=0;qr(a);
        a+=k;
        if((1.0*a/n) > 1.0*m) continue;
        ll _temp=(a-1)/m+1;ans^=_temp;
        _temp=(a-1)%m+1;
        ans^=_temp;
    }
    write(ans,'\n',true);
    return 0;
}

ll check() {
    rg ll k,sum=0,tg=0,i=1,tl=-2;
    while(i <= cnt) {
        if(tg <= 0) sum+=MU[i].x-1-tl,k=tl;
        tl=MU[i].x;
        while((i <= cnt) && (MU[i].x == tl)) tg+=MU[i].y,++i;
    }
    if(!sum) {puts("Impossible!");exit(0);}
    else if(sum > 1) {puts("Uncertain!");exit(0);}
    else return k+1;
}

Summary

多个区间的交难以维护，可以考虑维护区间补集的并集，最后求补集即为交集。