C基础 算法实现层面套路

引言 - 从实践狗讲起

　　理论到实践(有了算法到实现) 中间有很多过程. 算法方面本人啥也不懂, 只能说说实现方面. 例如下面

一个普通的插入排序.

//
// 插入排序默认从大到小
//
extern void sort_insert_int(int a[], int len) {
    int i, j;
    for (i = ; i < len; ++i) {
        int key = a[j = i];
        // 从小到大
        while (j >  && a[j - ] < key) {
            a[j] = a[j - ];
            --j;
        }
        a[j] = key;
    }
}

这时候有人就想了, 那数组是 double 的, 那怎么弄了. 也有一种解决方案

#define sort_insert(a, len) \
    _Generic(a
            , int *     : sort_insert_int
            , double *  : sort_insert_double
            , default   : sort_insert_default) (a, len)

是不是有所启发. 当然了. 对于上面是使用从大到小封装. 那如果需要从小到大呢. 可以这么做

static inline int _compare_2(const int left, const int key) {
    return left - key;
} 

extern void sort_insert_2(int a[], int len,
    int compare(const int left, const int key)) {
    int i, j;
    for (i = ; i < len; ++i) {
        int key = a[j = i];
        while (j >  && compare(a[j - ], key) < ) {
            a[j] = a[j - ];
            --j;
        }
        a[j] = key;
    }
}

单独把比较的行为抽象出来, 注册进去. 是不是很开心.

前言 - 细致一点封装

　　也许到这里会更开心. 既然能通过高科技泛型模拟出来. 那我们不也可以使用旧科技弄弄.

typedef int (* compare_f)(const void * left, const void * key);

static inline int _compare_3(const void * left, const void * key) {
    return *(int *)left - *(int *)key;
}

extern void sort_insert_3_(void * data, size_t ez, int len, compare_f compare) {
    char * a = data;
    void * key;
    int i, j;

    if ((key = malloc(ez)) == NULL)
        return;

    for (i = ; i < len; ++i) {
        memcpy(key, &a[i * ez], ez);
        for (j = i; j >  && compare(&a[(j - ) * ez], key) < ; --j)
            memcpy(&a[j * ez], &a[(j - ) * ez], ez);
        if (j != i)
            memcpy(&a[j * ez], key, ez);
    }

    free(key);
}

#define sort_insert_3(a, len, compare) \
    sort_insert_3_(a, sizeof(*(a)), len, (compare_f)compare)

是不是很巧妙, 一切都编程 void * 了.  当然了如果使用 C99 版本以上, 或者说用高版本的 GCC.

可以写的更好.

extern void sort_insert_4_(void * data, size_t ez, int len, compare_f compare) {
    char * a = data;
    char key[ez];
    int i, j;

    for (i = ; i < len; ++i) {
        memcpy(key, &a[i * ez], ez);
        for (j = i; j >  && compare(&a[(j - ) * ez], key) < ; --j)
            memcpy(&a[j * ez], &a[(j - ) * ez], ez);
        if (j != i)
            memcpy(&a[j * ez], key, ez);
    }
}

这里用了 C99 的 VLA 特性. 不知道细心的同学是否和思考. GCC 是怎么实现 VLA 可变长数组呢.

拨开云雾见青天, 我们不妨来个实验验证一哈. 看下面测试代码

#include <stdio.h>
#include <stdlib.h>

/*
 * file : vla.c
 * make : gcc -g -Wall -O2 -o vla.exe vla.c
 *
 */
int main(int argc, char * argv[]) {
    char a[];
    int b = ;
    char c[b];
    int * d = malloc(sizeof(int));
    if (d == NULL)
        exit(EXIT_FAILURE);
    *d = ;
    char e[*d];

    printf("%p : char a[10]\n", a);
    printf("%p : int b\n", &b);
    printf("%p : char c[b]\n", c);
    printf("%p : int * d\n", d);
    printf("%p : char e[*d]\n", e);

    free(d);
    return EXIT_SUCCESS;
}

最终输出结果是

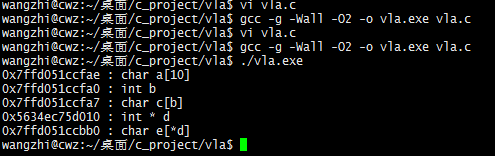
通过地址匹配对于 vla 可变数组, GCC是放在栈上的. 所有可以预测, 当可变数组大小太大. 函数栈会直接崩溃.

如果你有想法, 那么就去实现它, 多数简单我们还是能独立捉出来滴~~

正文 - 通用套路

　　还有一种套路, 采用宏模板去实现, 简单提一下这个思路. 看下面代码

#if defined(__T)

#define __f(type) sort_insert_##type
#define __F(type) __f(type)

static void __F(__T) (__T a[], int len, int compare(const __T left, const __T key)) {
    int i, j;
    for (i = ; i < (int)len; ++i) {
        __T key = a[j = i];
        while (j >  && compare(a[j - ], key) < ) {
            a[j] = a[j - ];
            --j;
        }
        a[j] = key;
    }
}

#endif

一般而言上面模板函数都会封装在一个局部文件中使用的时候也很方便, 例如下面这样

// 定义部分, 声明和定义分离可以自己搞
#undef  __T
#define __T int
#include "sort_insert.c"

// 使用部分和普通函数无异
sort_insert_int(a, LEN(a), _compare_2);

当然除了上面一种基于文件的函数模板. 还用一种纯基于函数宏的函数模板实现.

#define sort_insert_definition(T) \
    static void sort_insert_##T (T a[], int len, int compare(const T left, const T key)) { \
        int i, j; \
        for (i = ; i < len; ++i) { \
            T key = a[j = i]; \
            while (j >  && compare(a[j - ], key) < ) { \
                a[j] = a[j - ]; \
                --j; \
            } \
            a[j] = key; \
        } \
    }

sort_insert_definition(int)

使用还是一样  sort_insert_int(a, LEN(a), _compare_2); 跑起来. 第一种函数模板, 在嵌入式用的多.

第二种在实战中用的多, 对于处理各种算法相关的代码很普遍. 到这里应该可以理解上面那些

C 封装中一个小函数存在的套路.

后记 - 路越来越窄, 越来越清晰

错误是可以纠正的, 欢迎指正 ~ 表示感谢哈哈

<<啥时候成为津门第一呀>> : http://music.163.com/#/mv?id=197148

对不起 ~ 什么都明白的好晚 ~