20181030NOIP模拟赛T2

WYT的刷子

WYT有一把巨大的刷子，刷子的宽度为M米，现在WYT要使用这把大刷子去粉刷有N列的栅栏（每列宽度都为1米；每列的高度单位也为米，由输入数据给出）。

使用刷子的规则是：

1.与地面垂直，从栅栏的底部向上刷

2.每次刷的宽度为M米（当剩余栅栏宽度不够M米的话，刷子也可以使用，具体看样例2）

3.对于连续的M列栅栏，刷子从底向上，刷到的高度只能到这M列栅栏的最低高度。

WYT请你回答两个问题：

1、最少有多少个单位面积不能刷到（单位面积为1平米）

2、在满足第一问的条件下，最少刷几次？

输入

共两行：

第一行两个整数N和M。

第二行共N个整数，表示N列栅栏的高度

输出

一行，两个整数，分别为最少剩余的单位面积数量和最少刷的次数。

Input1:

5 3

5 3 4 4 5

Output1:

3

2

Input2:

10 3

3 3 3 3 3 3 3 3 3 3

Output2:

0

4

Input3:

7 4

1 2 3 4 3

Output3:

4

4

样例1的解释：

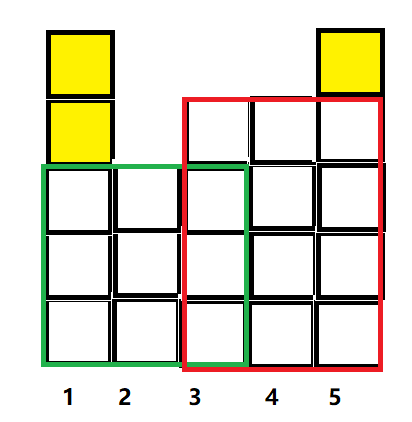
高度分别为       5     3    4     4     5

如上：

黄色的方块表示共有3个单位面积没刷上

绿色的框和红色的框表示一共刷了两次。

数据范围：

30%的数据：N<=10^3

50%的数据：N<=10^5

100%的数据：1<=N<=10^6, 1<=M<=10^6,N>=M, 每列栅栏的高度<=10^6.

思路：

单调栈裸题

利用和求最大子矩形一样的方法，我们可以用单调栈求出每个高度它对应的区间

如果这个区间小于m，则显然刷不到这个点的最高处

然后我们O(N)的扫三遍

第一遍判出哪些地方一定到不了最高点

第二遍和第三遍求出这些到达不了最高点的地方能达到多高

然后再O(n)扫一遍

就能得到有多少个涂不了色的了

至于涂得次数，贪心就好了

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rii register int i
#define rij register int j
using namespace std;
int n,m,zl[],r[],l[];
long long sum;
int sta[],top,sj[],bj[];
inline int rd(){
    register int x=,f=;char ch=getchar();
    while(!isdigit(ch)) {f=ch=='-'?:;ch=getchar();}
    while(isdigit(ch))  {x=(x<<)+(x<<)+ch-'';ch=getchar();}
    return f?x:-x;
}
int main()
{
    freopen("wyt.in","r",stdin);
    freopen("wyt.out","w",stdout);
    n=rd(),m=rd();
    for(rii=;i<=n;i++)
    {
        zl[i]=rd();
        sum+=zl[i];
    }
    for(rii=;i<=n;i++)
    {
        if(top==)
        {
            top++;
            sta[top]=i;
            continue;
        }
        while(zl[sta[top]]>zl[i])
        {
            r[sta[top]]=i-;
            top--;
        }
        top++;
        sta[top]=i;
    }
    while(top!=)
    {
        r[sta[top]]=n;
        top--;
    }
    for(rii=n;i>=;i--)
    {
        if(top==)
        {
            top++;
            sta[top]=i;
            continue;
        }
        while(zl[sta[top]]>zl[i])
        {
            l[sta[top]]=i+;
            top--;
        }
        top++;
        sta[top]=i;
    }
    while(top!=)
    {
        l[sta[top]]=;
        top--;
    }
    for(rii=;i<=n;i++)
    {
        if(r[i]-l[i]+<m)
        {
            bj[i]=;
        }
    }
    for(rii=;i<=n;i++)
    {
        if(bj[i]==)
        {
            sj[i]=sj[i-];
        }
        else
        {
            sj[i]=zl[i];
        }
    }
    for(rii=n;i>=;i--)
    {
        if(bj[i]==)
        {
            sj[i]=max(sj[i+],sj[i]);
        }
    }
    for(rii=;i<=n;i++)
    {
        sum-=sj[i];
    }
    cout<<sum<<endl;
    int ans=;
    int val=sj[],l=;
    for(rii=;i<=n;i++)
    {
        if(sj[i]!=val)
        {
            int sl=(i-l)/m;
            if(sl*m<(i-l))
            {
                sl++;
            }
            ans+=sl;
            l=i;
            val=sj[i];
        }
    }
    int sl=(n-l+)/m;
    if(sl*m<(n-l+))
    {
        sl++;
    }
    ans+=sl;
    cout<<ans;
    return ;
}