奇（qi）谋（ji）巧（yin）计（qiao）

一、打表法

0.http://oeis.org/

1.差分序列：https://blog.csdn.net/wu_tongtong/article/details/79115921

对于一个多项式产生的序列，可以多次求差分序列，直到差分序列均为0，这时原序列的表达式就可以表示为：

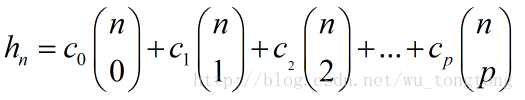
其中，c0……cp为差分表的第0条对角线。

同时有求和公式

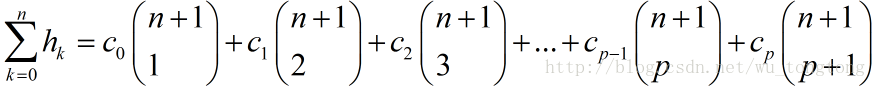
确定有公式后除去可以确定的项

#include <bits/stdc++.h>
 
using namespace std;
#define rep(i, a, n) for (ll i=a;i<n;i++)
#define SZ(x) ((ll)(x).size())
typedef long long ll;
const ll mod = ;
 
ll powmod(ll a, ll b) {
    ll res = ;
    a %= mod;
    for (; b; b >>= ) {
        if (b & )res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}
 
ll n;
namespace linear_seq {
    const ll N = ;
    ll res[N], base[N], _c[N], _md[N];
 
    vector<ll> Md;
 
    void mul(ll *a, const ll *b, ll k) {
        rep(i, , k + k) _c[i] = ;
        rep(i, , k) if (a[i]) rep(j, , k) _c[i + j] = (_c[i + j] + a[i] * b[j]) % mod;
        for (ll i = k + k - ; i >= k; i--)
            if (_c[i])
                rep(j, , SZ(Md)) _c[i - k + Md[j]] = (_c[i - k + Md[j]] - _c[i] * _md[Md[j]]) % mod;
        rep(i, , k) a[i] = _c[i];
    }
 
    ll solve(ll n, vector<ll> a, vector<ll> b) {
        ll ans = , pnt = ;
        ll k = SZ(a);
        rep(i, , k) _md[k -  - i] = -a[i];
        _md[k] = ;
        Md.clear();
        rep(i, , k) if (_md[i] != ) Md.push_back(i);
        rep(i, , k) res[i] = base[i] = ;
        res[] = ;
        while (1ll << pnt <= n) pnt++;
        for (ll p = pnt; p >= ; p--) {
            mul(res, res, k);
            if (n >> p & ) {
                for (ll i = k - ; i >= ; i--) res[i + ] = res[i];
                res[] = ;
                rep(j, , SZ(Md)) res[Md[j]] = (res[Md[j]] - res[k] * _md[Md[j]]) % mod;
            }
        }
        rep(i, , k) ans = (ans + res[i] * b[i]) % mod;
        if (ans < ) ans += mod;
        return ans;
    }
 
    vector<ll> BM(vector<ll> s) {
        vector<ll> C(, ), B(, );
        ll L = , m = , b = ;
        rep(n, , SZ(s)) {
            ll d = ;
            rep(i, , L + ) d = (d + (ll) C[i] * s[n - i]) % mod;
            if (d == ) ++m;
            else if ( * L <= n) {
                vector<ll> T = C;
                ll c = mod - d * powmod(b, mod - ) % mod;
                while (SZ(C) < SZ(B) + m) C.push_back();
                rep(i, , SZ(B)) C[i + m] = (C[i + m] + c * B[i]) % mod;
                L = n +  - L;
                B = T;
                b = d;
                m = ;
            } else {
                ll c = mod - d * powmod(b, mod - ) % mod;
                while (SZ(C) < SZ(B) + m) C.push_back();
                rep(i, , SZ(B)) C[i + m] = (C[i + m] + c * B[i]) % mod;
                ++m;
            }
        }
        return C;
    }
 
    vector<ll> temp;
 
    void init(vector<ll> a) {
        temp = BM(a);
        temp.erase(temp.begin());
        rep(i, , SZ(temp))temp[i] = (mod - temp[i]) % mod;
    }
 
    ll gao(vector<ll> a, ll n) {
        return solve(n, temp, vector<ll>(a.begin(), a.begin() + SZ(temp)));
    }
};
using namespace linear_seq;
 
int main() {
 
    vector<ll> v;
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    v.push_back();
    init(v);
    ll T;
    scanf("%lld", &T);
    while (T--) {
        ll n;
        scanf("%lld", &n);
        printf("%lld\n", gao(v, n - ));
    }
    return ;
}

递推