[POI2012] BEZ-Minimalist Security

一张n个点m条边的无向图，有点权有边权都是非负，且每条边的权值小于等于两个顶点的权值和，现在要将每个点减一个非负整数使得每条边权等于两个顶点的点权和，问最大修改代价和最小修改代价

思路神的一匹，完全想不出来，对着题解想了半天才有点理解

首先有一个小结论：对于一个联通块，如果一个顶点的值确定了，其余顶点的值都能确定。这是显然的，因为直接用一条边的边权减去已知点权就是另一个点的权值。如果我们设一个点的权值为x，与之相连的边权为w，另一点点权即为w-x

这样的话其实整个联通块内所有的点权都可以表示成y=k*x+b(k∈(-1,1))的形式，我们对于解一下关于y的不等式即可

特别注意的是，如果图中存在奇环，那么某个点会存在两种系数不同的表示，这时我们直接解这个方程就可以求出x的唯一解

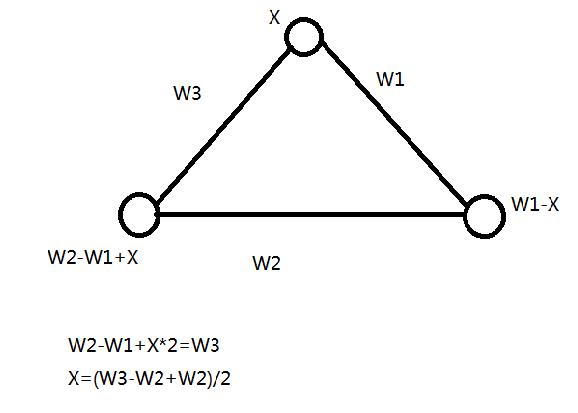
这时我们还得保证x解出来为整数，这也是做这个题目要注意的的一点

代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 #include<cstdlib>
 #define N 300010
 #define M 5000010
 #define ll long long
 using namespace std;
 queue<int>qx,qy;

 int n,m,num;
 int head[N],val[N],q[N];
 bool vis[N][];
 ll ans1,ans2,v[N][];

 int read()
 {
     char ch=getchar(); int f=,x=;
     while(ch>''||ch<'') {if(ch=='-') f=-; ch=getchar();}
     while(ch>=''&&ch<='') x=x*+ch-'',ch=getchar();
     return x*f;
 }

 struct point{
     int next,to,dis;
 }e[M<<];

 void add(int from,int to,int dis)
 {
     e[++num].next=head[from];
     e[num].to=to;
     e[num].dis=dis;
     head[from]=num;
 }

 void bfs(int x)
 {
     vis[x][]=;
     qx.push(x); qy.push();
     int tot=; q[++tot]=x;
     while(!qx.empty())
     {
         int a=qx.front(),b=qy.front();
         qx.pop(); qy.pop();
         for(int i=head[a];i;i=e[i].next)
         {
             int to=e[i].to;
             if(!vis[to][]&&!vis[to][]) q[++tot]=to;
             if(vis[to][b^])
             {
                 if(v[to][b^]!=e[i].dis-v[a][b]) {printf("NIE"); exit();}
             }
             else
             {
                 vis[to][b^]=,v[to][b^]=e[i].dis-v[a][b];
                 qx.push(to); qy.push(b^);
             }
         }
     }
     ll L=,R=val[x],sum1=,sum2=;
     for(int i=;i<=tot;i++)
     {
         int a=q[i];
         if(vis[a][]) L=max(L,-v[a][]),R=min(R,val[a]-v[a][]);
         if(vis[a][]) L=max(L,v[a][]-val[a]),R=min(R,v[a][]);
         if(vis[a][]&&vis[a][])
         {
             if((v[a][]-v[a][])&) {printf("NIE"); exit();}
             L=max(L,(v[a][]-v[a][])>>);
             R=min(R,(v[a][]-v[a][])>>);
         }
     }
     if(L>R) {printf("NIE"); exit();}
     for(int i=;i<=tot;i++)
     {
         int a=q[i];
         if(vis[a][]) sum1+=val[a]-L-v[a][],sum2+=val[a]-R-v[a][];
         else sum1+=val[a]+L-v[a][],sum2+=val[a]+R-v[a][];
     }
     if(sum1>sum2) swap(sum1,sum2);
     ans1+=sum1,ans2+=sum2;
 }

 int main()
 {
     n=read(); m=read();
     for(int i=;i<=n;i++) val[i]=read();
     for(int i=;i<=m;i++)
     {
         int x=read(),y=read(),z=read();
         add(x,y,z); add(y,x,z);
     }
     for(int i=;i<=n;i++)
         if(!vis[i][]&&!vis[i][])
             bfs(i);
     printf("%lld %lld",ans1,ans2);
     return ;
 }