【欧拉回路】【欧拉路径】【Fleury算法】CDOJ1634 记得小苹初见，两重心字罗衣

Fleury算法看这里 http://hihocoder.com/problemset/problem/1181

把每个点看成边，每个横纵坐标看成一个点，得到一个无向图.

如果新图中每个点的度都是偶数，那么就是一个欧拉图，对该图跑一遍欧拉回路，对走过的边轮流染色，就可以保证每个点所连的边的红蓝颜色相等.

如果存在度数为奇数的点，新建两个点a和b.把横坐标的度数为奇数的点和a连边，把纵坐标为奇数的点和b连边，这样最多只有a和b的度数为奇数，可以跑欧拉路径.

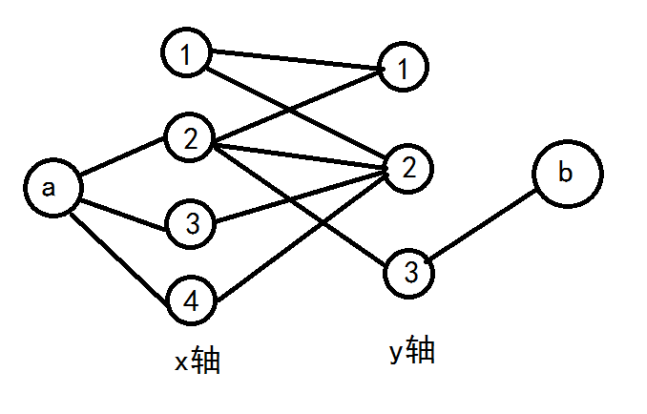
注意Fleury算法的时候，要及时把访问过的边从图中删去（真的删去而不是打标记），否则重复访问会导致复杂度飙升。

#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
struct Edge{
	int v,id;
};
vector<Edge>G[400010];
int n,S,T;
bool anss[200010],pen,vis[600010];
inline void dfs(int U){
	while(!G[U].empty()){
		Edge e=G[U].back();
		G[U].pop_back();
		if(!vis[e.id]){
			vis[e.id]=1;
			dfs(e.v);
			if(e.id<=n){
				anss[e.id]=pen;
				pen^=1;
			}
		}
	}
}
int main(){
//	freopen("c.in","r",stdin);
	int x,y;
	scanf("%d",&n);
	S=400001; T=400002;
	for(int i=1;i<=n;++i){
		scanf("%d%d",&x,&y);
		G[x].push_back((Edge){y+200000,i});
		G[y+200000].push_back((Edge){x,i});
	}
	int cnt=n;
	for(int i=1;i<=200000;++i){
		if(G[i].size()&1){
			G[S].push_back((Edge){i,++cnt});
			G[i].push_back((Edge){S,cnt});
		}
	}
	for(int i=200001;i<=400000;++i){
		if(G[i].size()&1){
			G[i].push_back((Edge){T,++cnt});
			G[T].push_back((Edge){i,cnt});
		}
	}
	if(G[S].size()&1){
		dfs(S);
	}
	if(!G[T].empty()){
		dfs(T);
	}
	for(int i=1;i<=200000;++i){
		if(!G[i].empty()){
			dfs(i);
		}
	}
	for(int i=1;i<=n;++i){
		putchar(anss[i] ? 'r' : 'b');
	}
	puts("");
	return 0;
}